Урок однієї задачі (Геометрія)
Про матеріал
Урок однієї задачі з геометрії, 9клас.
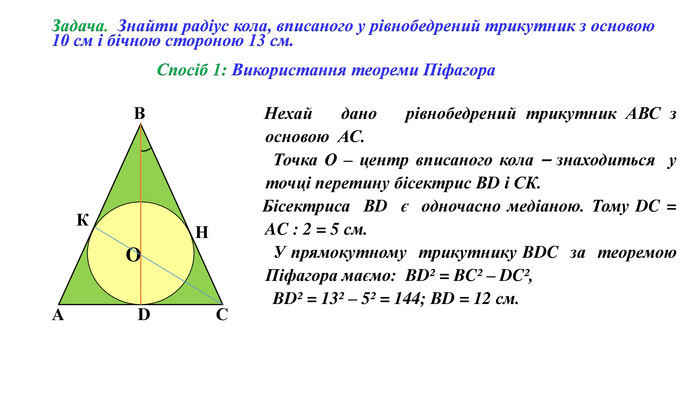
Знайти радіус кола, вписаного у рівнобедрений трикутник з основою 10 см і бічною стороною 13 см.
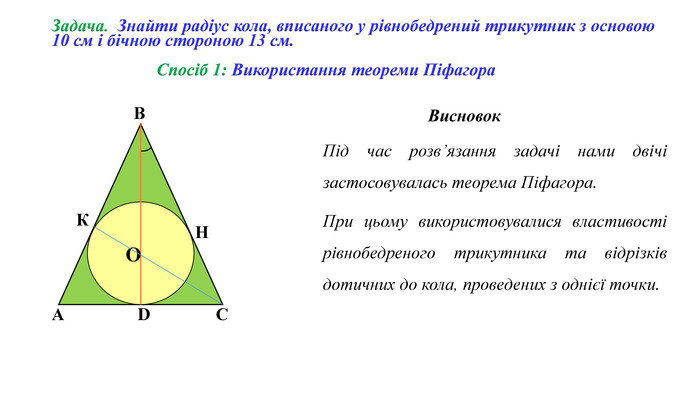
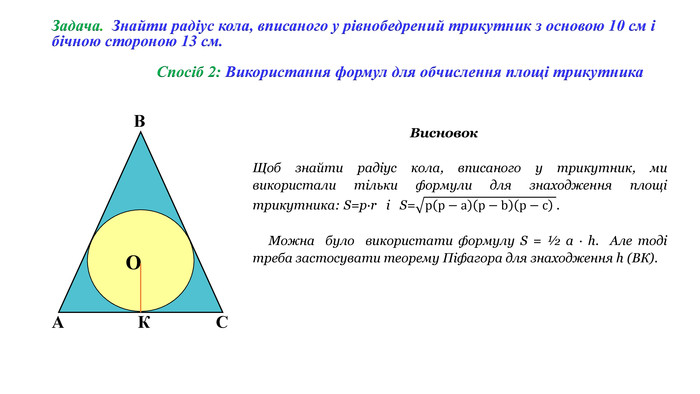
Спосіб 1: Використання теореми ПіфагораСпосіб 2: Використання формул для обчислення площі трикутника
Спосіб 3: Тригонометричні функції гострого кута
Спосіб 4: Властивості бісектрис у трикутнку
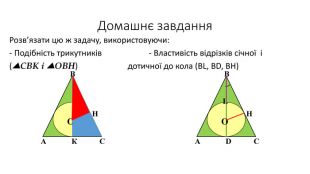
Д/З: подібність трикутників і властивість січної і дотичної до кола
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку