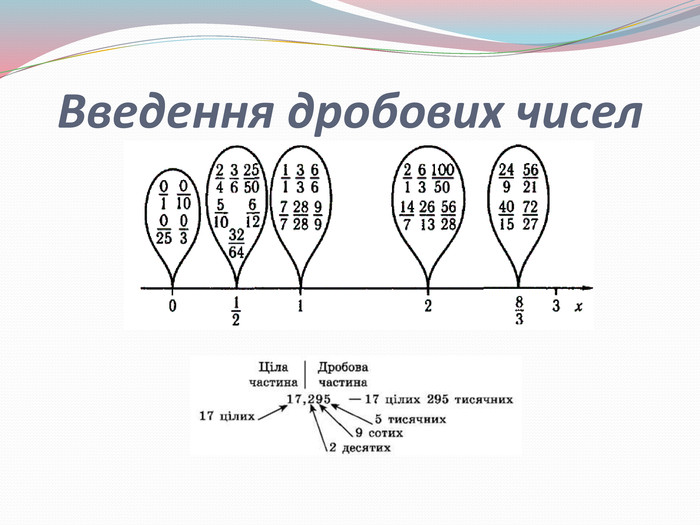
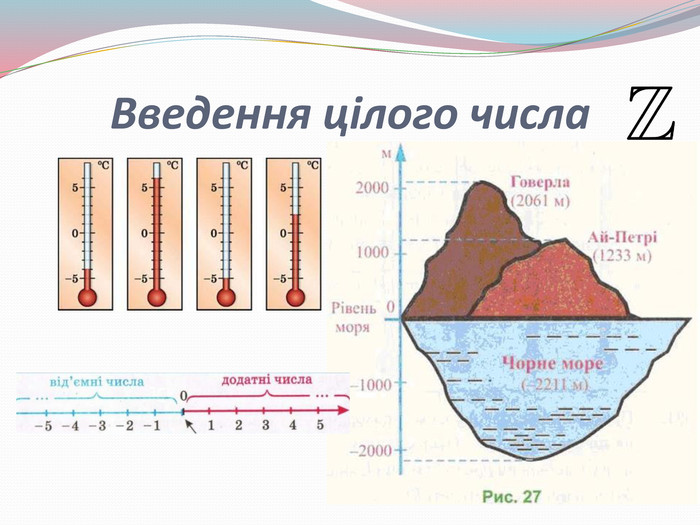
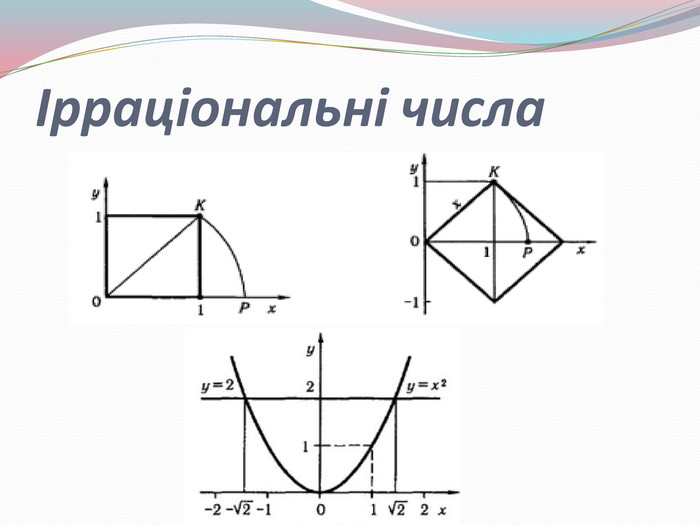
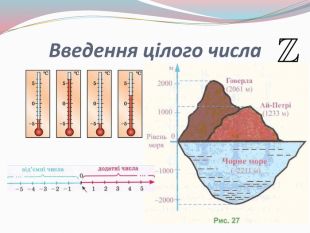
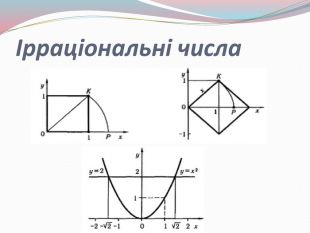
Презентація "Розвиток поняття про число"
Про матеріал
Числа - це невід'ємне знаряддя сучасної цивілізації, що використовується для впорядкування сфери її діяльності.
Пам'ять людства не зберегла, що не донесла до нас ім'я винахідника колеса або гончарного круга. Це й не дивно: більше 10 тис. Років пройшло з тих пір, як люди всерйоз зайнялися землеробством, скотарством і виробництвом найпростіших товарів. Назвати ж ім'я генія, вперше який поставив питанням "скільки?", Тим більше, неможливо. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку