Презентація "Середні пропорційні відрізки у трикутнику"
Про матеріал
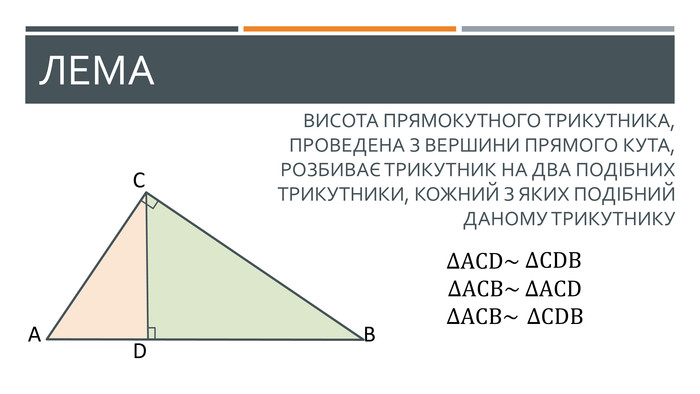
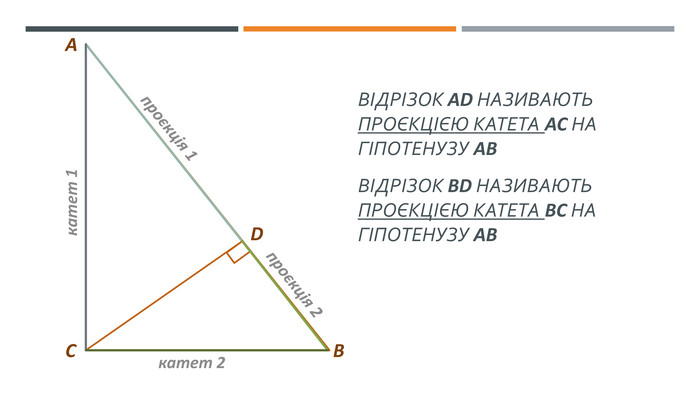
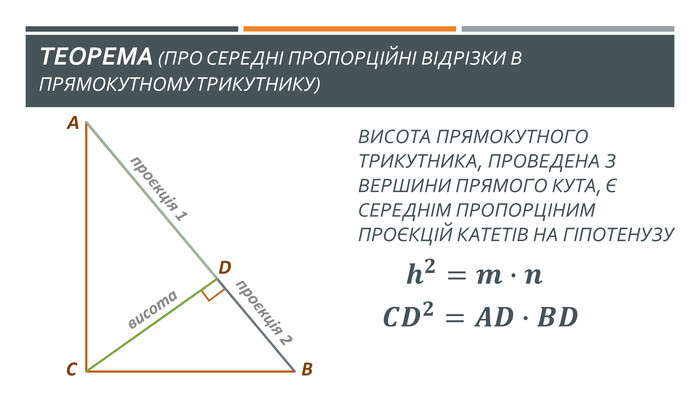
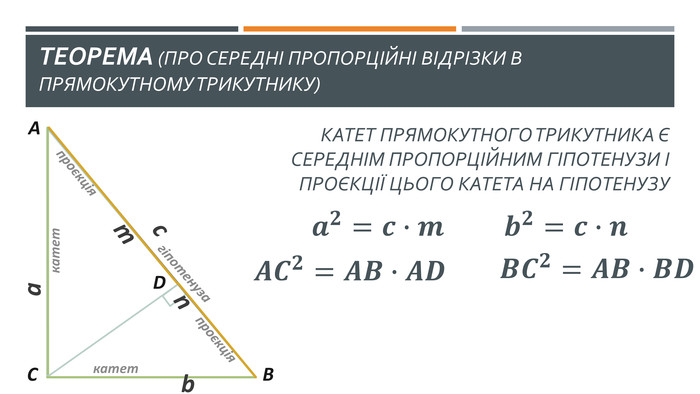
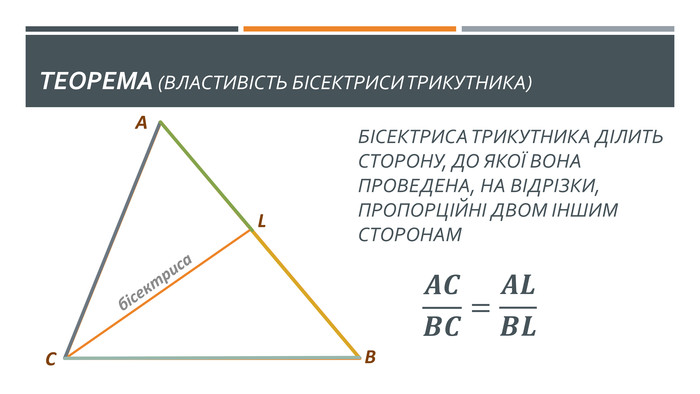
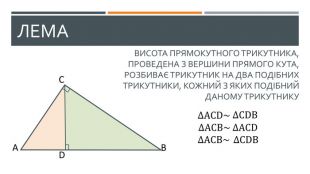
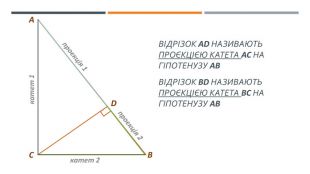
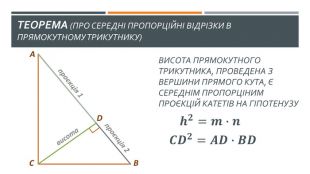
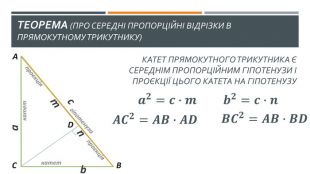
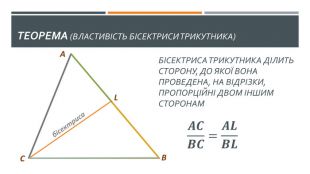
У презентації висвітлено наступні теми: 1. "Теорема про середні пропорційні відрізки у прямокутному трикутнику (про висоту та про катет)" 2. "Теорема про властивість бісетриси трикутника" Слайди доречно анімовано
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку





-

Теліга Олена
13.12.2023 в 19:50
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Іменинник Людмила Миколаївна
11.12.2023 в 09:45
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Мартись Юлія Валеріївна
16.01.2023 в 20:09
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Опанасенко Віталіна Іванівна
15.12.2022 в 10:20
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Бондар Олена
10.12.2021 в 05:07
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 2 відгука