Презентація Степенева функція

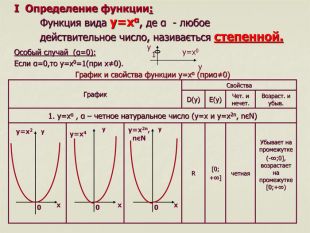
![y y y=x0 1 Убывает на промежутке (-∞;0], возрастает на промежутке [0;+∞) четная [0; +∞] R 1. y=xα , α – четное натуральное число (y=x и y=x2n, nєN) Возраст. и убыв. Чет. и нечет. E(y) D(y) Свойства График y=x2 0 x y y y x x 0 0 y=x4 y=x2n, nєN I Определение функции: Функция вида y=xα, де α - любое действительное число, називається степенной. Особый случай (α=0): Если α=0,то y=x0=1(при x≠0). График и свойства функции y=xα (приα≠0) y y y=x0 1 Убывает на промежутке (-∞;0], возрастает на промежутке [0;+∞) четная [0; +∞] R 1. y=xα , α – четное натуральное число (y=x и y=x2n, nєN) Возраст. и убыв. Чет. и нечет. E(y) D(y) Свойства График y=x2 0 x y y y x x 0 0 y=x4 y=x2n, nєN I Определение функции: Функция вида y=xα, де α - любое действительное число, називається степенной. Особый случай (α=0): Если α=0,то y=x0=1(при x≠0). График и свойства функции y=xα (приα≠0)](/uploads/files/461847/112281/119829_images/2.jpg)
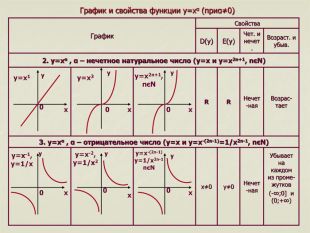
![3. y=xα , α – отрицательное число (y=x и y=x-(2n-1)=1/x2n-1, nєN) Возрас-тает Нечет-ная R R Убывает на каждом из проме-жутков (-∞;0] и (0;+∞) Нечет-ная y≠0 x≠0 2. y=xα , α – нечетное натуральное число (y=x и y=x2n+1, nєN) Возраст. и убыв. Чет. и нечет. E(y) D(y) Свойства График y y y y y y x x x x x x 0 0 0 0 0 0 y=x-2,
y=1/x2 y=x-(2n-1) y=1/x2n-1 nєN y=x-1,
y=1/x y=x2n+1, nєN y=x3 y=x1 График и свойства функции y=xα (приα≠0) 3. y=xα , α – отрицательное число (y=x и y=x-(2n-1)=1/x2n-1, nєN) Возрас-тает Нечет-ная R R Убывает на каждом из проме-жутков (-∞;0] и (0;+∞) Нечет-ная y≠0 x≠0 2. y=xα , α – нечетное натуральное число (y=x и y=x2n+1, nєN) Возраст. и убыв. Чет. и нечет. E(y) D(y) Свойства График y y y y y y x x x x x x 0 0 0 0 0 0 y=x-2,
y=1/x2 y=x-(2n-1) y=1/x2n-1 nєN y=x-1,
y=1/x y=x2n+1, nєN y=x3 y=x1 График и свойства функции y=xα (приα≠0)](/uploads/files/461847/112281/119829_images/3.jpg)














y y y=x0 1 Убывает на промежутке (-∞;0], возрастает на промежутке [0;+∞) четная [0; +∞] R 1. y=xα , α – четное натуральное число (y=x и y=x2n, nєN) Возраст. и убыв. Чет. и нечет. E(y) D(y) Свойства График y=x2 0 x y y y x x 0 0 y=x4 y=x2n, nєN I Определение функции: Функция вида y=xα, де α - любое действительное число, називається степенной. Особый случай (α=0): Если α=0,то y=x0=1(при x≠0). График и свойства функции y=xα (приα≠0)
3. y=xα , α – отрицательное число (y=x и y=x-(2n-1)=1/x2n-1, nєN) Возрас-тает Нечет-ная R R Убывает на каждом из проме-жутков (-∞;0] и (0;+∞) Нечет-ная y≠0 x≠0 2. y=xα , α – нечетное натуральное число (y=x и y=x2n+1, nєN) Возраст. и убыв. Чет. и нечет. E(y) D(y) Свойства График y y y y y y x x x x x x 0 0 0 0 0 0 y=x-2, y=1/x2 y=x-(2n-1) y=1/x2n-1 nєN y=x-1, y=1/x y=x2n+1, nєN y=x3 y=x1 График и свойства функции y=xα (приα≠0)
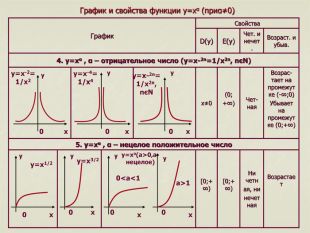
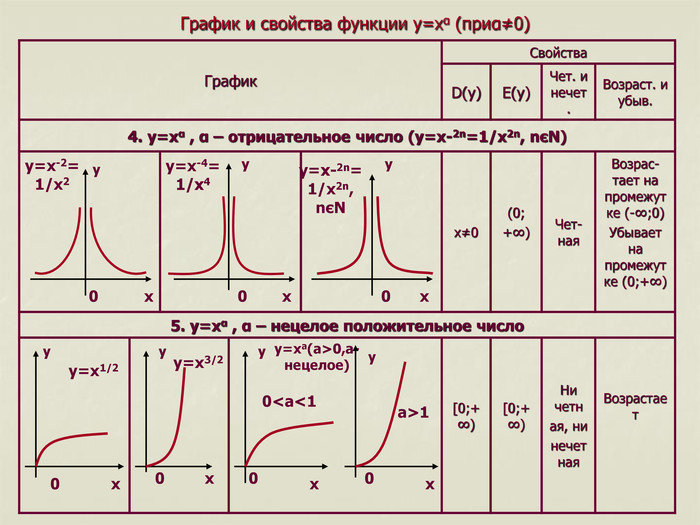
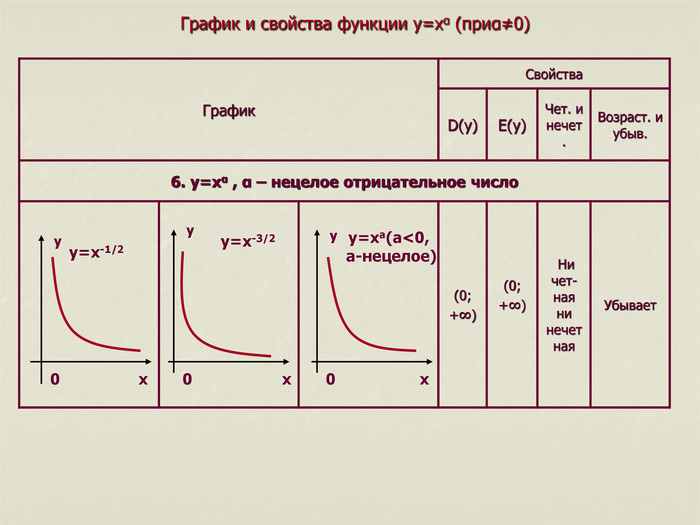
5. y=xα , α – нецелое положительное число Возрас-тает на промежутке (-∞;0) Убывает на промежутке (0;+∞) Чет-ная (0; +∞) x≠0 Возрастает Ни четн ая, ни нечетная [0;+∞) [0;+∞) 4. y=xα , α – отрицательное число (y=x-2n=1/x2n, nєN) Возраст. и убыв. Чет. и нечет. E(y) D(y) Свойства График y y y y y y x x x x x x 0 0 0 0 0 0
y=x3/2
y=xa(a>0,a- нецелое)
y=x1/2
y=x-2n= 1/x2n, nєN y=x-4=
1/x4 y=x-2=
1/x2 x y 0 a>1 0
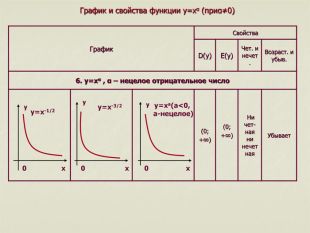
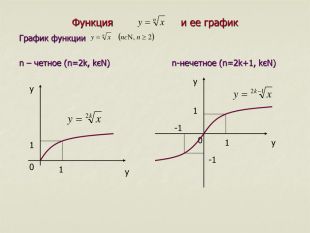
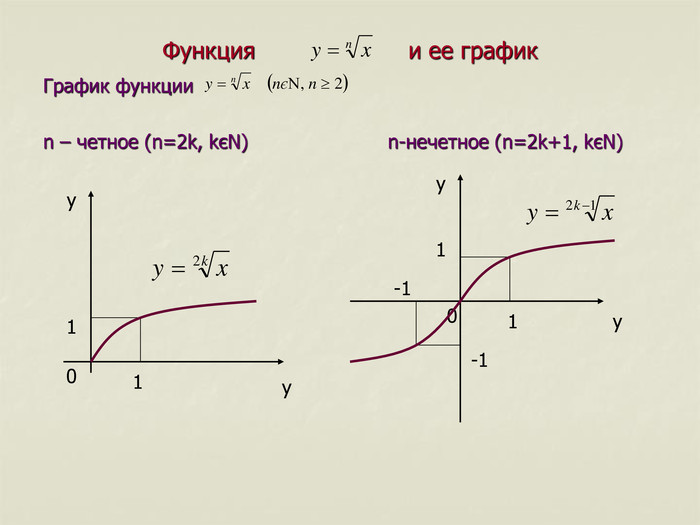
7. Промежутки знакопостоянства: при x>0 значение y>0, при x<0 знач. y<0 7. Промежутки знакопостоянства: при x>0 значение y>0 6. Промежутки возраст. и убыв.: на всей области определения функция возрастает. 5. Точки пересечения с осями координат: График проходит через начало координат 4. Функция является нечетной: , следовательно, график функции симметричен относительно начала координат. 4. Функция не является ни четной, ни нечетной. 3. Наибольшего и наименьшего значений функция не имеет. 3. Наибольшего значения функция не имеет; наименьшее значение – y=0 (при x=0). 2. Область значений: yєR(y-любое действительное число), то есть 2. Область значений: y≥0, то есть 1. Область определения: xєR(x-любое действительное число),то есть 1. Область определения: x≥0, то есть n-нечетное (n=2k+1, kєN) n-четное (n=2k, kєN) Свойства функции
Корень n-ой степени Квадратный корень существует только при а≥0(kєN) существует при любых значениях а существует только при а≥0 2. Область допустимых значений Арифметический корень- неотрицательное значение корня. При а≥0: обозначение арифметического значени корня Корнем n-ой степени из числа а называется такое число b, n-ая степень которого равен а. Если а=bn(nєN,n≠1), то b – корень n-ой степни из числа а. Квадратным корнем из числа а называется такое число b, квадрат которого равен а. Если а=b2, то b – квадратный корень из числа а. Корень n-ой степени Квадратный корень 1. Определение Корень n-ой степени и его свойства
n=2k - четное n=2k+1 - нечетное 3. Свойства корня n - степени Уравнение x8=7 имеет корни Уравнение x8=-7 не имеет корней Уравнение x5=3 имеет единственный корень Примеры При а>0 все корни уравнения x2k=a можно записать так При а=0 уравнение x2k=a не имеет корней При любых значениях а уравнение x2k+1=a имеет единственный корень n=2k - четное (kєN) n=2k+1 - нечетное (kєN) Запись решений уравнения xn=a(nєN)
Для произвольных значений n и k (nєN, n≠1,kєN) 3) При а ≥0 4) При а ≥0 5) При а ≥0, b ≥0 Следствия При а ≥0, b ≥0 При а ≥0, b ≥0 вынесение множителя внесение множителя из-под знака корня под знак корня 6) При а ≥0, b ≥0 7) При а ≥0 основное свойство корня Значение корня из степени неотрицательного числа не изменится, если показатель корня и показатель подкоренного выражения умножить (или разделить) на одно и то же натуральное число. 8) При а ≥0, b ≥0, если a>b? то
Пример 2 Пример 1 При возведении обеих частей уравнения в четную степень, могут появиться посторонние корни, которые отсеиваются проверкой. При возведении обеих частей уравнения в нечетную степень, получаем уравнение, равнесильное данному (на его ОДЗ) 1. С помощью возведения обеих частей уравнения в одну и ту же степень Решение иррациональных уравнений Уравнения, в которых переменная находится под знаком корня, называется иррациональным . При решении иррациональное уравнение чаще всего сводят к рациональному уравнению с помощью некоторых преобразований. Понятие иррационального уравнения III Уравнения и их решения
2. Оценка значений левой и правой частей уравнения Ориентир Пример f(x)=g(x) f(x)=a, f(x)≥a, g(x)=a g(x)≤a Если требуется решить уравнение Вида f(x)=g(x) и выяснилось, что f(x)≥a, g(x)≤a, то равенство между левой и правой частями уравнения возможно лишь в случае, если f(x) и g(x) одновременно равны а.
x 0 -4 IV Неравенства и их решения 1. Метод интервалов (для неравенств вида f(x)≥0) Ориентир Пример Найти ОДЗ неравенства. Найти нули функции f(x) (f(x)=0). Отметить нули функции на ОДЗ и найти знак функции на каждом из промежутков, на которые разбивается ОДЗ. Записать ответ, учитывая знак неравенства.
2) Если обе части неравенства неотрицательны, то при возведении обеих частей неравенства в четную степень (с сохранением знака неравенства), получаем неравенство, равносильное данному (на ОДЗ заданного неравенства). 1) При возведении обеих частей неравенства в нечетную степень (с сохранением знака неравенства), получаем неравенство, равносильное данному (на ОДЗ данного неравенства). 2. Равносильные преобразования

про публікацію авторської розробки
Додати розробку