•    ФОРМУВАННЯ КОМПЕТЕНТНОСТЕЙ:

1.                     ПРЕДМЕТНА КОМПЕТЕНТНІСТЬ: СИСТЕМАТИЗУВАТИ  ВІДОМОСТІ  ПРО  ТРИКУТНИКИ;  ВІДКРИТИ  ДОСЛІДНИМ  ШЛЯХОМ  ТЕОРЕМУ  ПРО  СУМУ  КУТІВ  ТРИКУТНИКА,  ФОРМУВАТИ  НАВИЧКИ  ЗНАХОДЖЕННЯ  РІЗНИХ  СПОСОБІВ  ДОВЕДЕННЯ  ЦІЄЇ  ТЕОРЕМИ;

СФОРМУВАТИ ВМІННЯ  ВИКОНУВАТИ ЗАВДАННЯ,  У ЯКИХ  ПЕРЕДБАЧЕНО ВИКОНАННЯ ВЛАСТИВОСТІ СУМИ КУТІВ ТРИКУТНИКА; СФОРМУВАТИ ПОНЯТТЯ ЗОВНІШНЬОГО КУТА; 2. КЛЮЧОВІ КОМПЕТЕНТНОСТІ:

А) СПІЛКУВАННЯ ДЕРЖАВНОЮ МОВОЮ – ГРАМОТНО ВИСЛОВЛЮВАТИСЯ РІДНОЮ МОВОЮ; ДОРЕЧНО ТА КОРЕКТНО ВЖИВАТИ В МОВЛЕННІ МАТЕМАТИЧНУ ТЕРМІНОЛОГІЮ;

Б) ІНФОРМАЦІЙНО-ЦИФРОВА КОМПЕТЕНТНІСТЬ – СТРУКТУРУВАТИ ДАНІ, ДІЯТИ ЗА

АЛГОРИТМОМ; ПОКАЗАТИ  ЗАСТОСУВАННЯ  НАБУТИХ  ЗНАНЬ  У  ПРАКТИЧНІЙ  ДІЯЛЬНОСТІ;

В) УМІННЯ ВЧИТИСЯ ВПРОДОВЖ ЖИТТЯ – ВИЗНАЧИТИ МЕТУ НАВЧАЛЬНОЇ ДІЯЛЬНОСТІ,  ВІДБИРАТИ Й ЗАСТОСОВУВАТИ ПОТРІБНІ ЗНАННЯ ТА СПОСОБИ ДІЯЛЬНОСТІ ДЛЯ ДОСЯГНЕННЯ ЦІЄЇ МЕТИ.

Хід уроку І. Організаційний момент.

ІІ. Перевірка домашнього завдання.

Учні звіряють свої результати з готовими відповідями підготовленими на дошці і роблять позначки залежно від правильності результатів.

ІІІ.  Актуалізація  опорних  знань. Фронтальне опитування.

1.    Основна властивість вимірювання кутів.

2.    Який кут називається прямим, тупим, гострим, розгорнутим?

3.    Що таке трикутник?

4.    Який трикутник називається прямокутним, тупокутним, гострокутним?

5.    Який трикутник називається рівнобедреним, рівностороннім, різностороннім?

6.    Властивості рівнобедреного, рівностороннього трикутників?

7.    Властивості кутів утворених перетином паралельних прямих січною.

ІV. Мотивація  навчальної  діяльності.

Ви  тільки  розпочали  вивчати  геометрію,  але  вже  знаєте  назви  елементів  трикутників  та  їх  види,  а  також  ознаки  рівності  трикутників.

Трикутник  відіграє   в  геометрії  особливу  роль.  Без  перебільшення  можна  сказати ,  що  вся  геометрія  з  часів  “Начал”  Евкліда  базується  на  “трьох  китах” – трьох  ознаках  рівності  трикутників. За  декілька  тисячоліть 

геометри  так  детально  вивчили  трикутник,  що  деколи  говорять  про 

“геометрію  трикутника”  як  про  самостійний  розділ елементарної  геометрії.

Серед  усіх  метричних  властивостей  трикутника,  які  вивчаються  у  7 – му  класі,  найважливішою  є  властивість  суми  кутів  трикутника.

V. Вивчення  нового  матеріалу.

Проблемна ситуація

Учитель. Перед вами два трикутника: великий і малий.

. Чи однакова сума кутів цих трикутників? ( учні висувають свої припущення) Учитель. Перед вами три трикутника: гострокутний, прямокутний та тупокутний.

. Чи однакова сума кутів цих трикутників? ( учні висувають свої припущення)

Учитель. Перед вами три трикутника: рівнобедрений, рівносторонній, різносторонній.

. Чи однакова сума кутів цих трикутників? ( учні висувають свої припущення)

Завдання №1 (дослідницька робота)

Учні отримують різні види трикутників і за допомогою транспортира вимірюють градусні міри кутів та знаходять їх суму.

(Учні,  виконують  завдання , працюючи у  парах. Результати  роботи       кожної  групи  записуються  на  дошці).

Висновок. Учитель. Як  ви  думаєте,  чи  випадково  сума  кутів  трикутника  виявилась  близькою  до  180°?

Завдання 2.

Проведемо  експеримент :  знайдемо  суму  кутів  трикутника  за  допомогою  перегинання  його  паперової  моделі.

Висновок.

Учитель.   Як  бачимо,  кути  трикутника  утворили  розгорнутий  кут,  градусна  міра  якого  дорівнює  180°. Властивість  суми  кутів  трикутника  характерна  тим,  що  вона  зовсім  не  очевидна.  До  того  ж,  трикутники  можуть  бути  найрізноманітнішими - від  маленьких,  які  ми  будуємо  в  зошитах,  до  велетенських,  які  можна  побудувати  на  поверхні  Землі  чи  уявити,  з’єднавши  відрізками  три  зорі  на  небі.  Для  всіх  цих  трикутників  справедлива  одна  й  та  сама  рівність.

Історична довідка

Властивість суми кутів трикутника було встановлено  дослідним шляхом, ще в стародавньому Єгипті. Але відомості які дійшли до нас про доведення більш пізнішого часу. Доведення було відкрито Піфагорійцями в п’ятому столітті до нашої ери. Доведемо  теорему  про  суму  кутів  трикутника.

Теорема.  Сума  кутів  трикутника  дорівнює  180° .

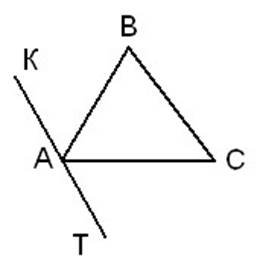Дано:  АВС,  ےА,  ےВ,  ےС.

Довести:  ےА+ ےВ+ ےС=180°.

Доведення

1) Проведемо  через  вершину  А  довільного  трикутника  АВС  пряму  КТ,  паралельно  прямій  ВС .

Через точку, яка не лежить на прямій, проходить одна пряма, яка паралельна даній прямій KT ║ BC(аксіома паралельних прямих). 2)Точка А вершина розгорнутого кута KAT, ےKAT=180⁰. Промені АВ і ВС ділять кут КАT на три частини. За аксіомою вимірювання кутів: ےKAT= ےKAB+ےBAC+ےCAT. 3) KT║BC, а дві інші сторони трикутника АВ і АС при двох паралельних прямих KT i BC є січними.

ВИКОРИСТАЄМО ВЛАСТИВІСТЬ ПАРАЛЕЛЬНИХ ПРЯМИХ СКЛАДЕМО ПАРИ РІВНИХ КУТІВ.

KT ║ BC, АВ – СІЧНА →  ےКАВ=ےВ KT ║ BC, АС – СІЧНА →  ےCAT=ےC

МИ З ВАМИ ПОКАЗАЛИ, ЩО ВЕЛИЧИНА РОЗГОРНУТОГО КУТА СКЛАДАЄТЬСЯ ІЗ

УСІХ ТРЬОХ КУТІВ ТРИКУТНИКА, ТОБТО ВСІ ТРИ КУТИ ТРИКУТНИКА

ВКЛАЛИСЬ У РОЗГОРНУТИЙ КУТ, А ВЕЛИЧИНА РОЗГОРНУТОГО  ےКАТ=180⁰, ТОМУ  ےА+ےВ+ےС=180⁰.

ТЕОРЕМУ ДОВЕДЕНО.

УСНІ ВПРАВИ

1.    ЧИ МОЖУТЬ У ТРИКУТНИКУ БУТИ ДВА ТУПИХ КУТА?  (НІ)

2.    ЧИ МОЖУТЬ У ТРИКУТНИКУ БУТИ ДВА ПРЯМИХ КУТА?    (НІ)3. ЧИ МОЖУТЬ У ТРИКУТНИКУ БУТИ ТУПИЙ І ПРЯМИЙ КУТИ?  (НІ) НАСЛІДКИ.

1)    ТРИКУТНИК НЕ МОЖЕ МАТИ ДВОХ ПРЯМИХ АБО ДВОХ ТУПИХ КУТІВ.

2)    У КОЖНОМУ ТРИКУТНИКУ ПРИНАЙМНІ  ДВА КУТИ – ГОСТРІ.

КРІМ ВНУТРІШНІХ КУТІВ ТРИКУТНИК МАЄ ЩЕ Й ЗОВНІШНІ КУТИ.

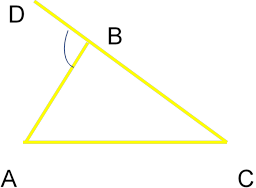Означення. Кут, суміжний із внутрішнім кутом трикутника, називається зовнішнім кутом трикутника при даній вершині.

 ےABD – зовнішній кут ∆ АВС.

Теорема. Зовнішній кут трикутника  дорівнює сумі двох внутрішніх кутів  трикутника , не суміжних з ним.  ےАВD =  ےBAC +ےАСВ.

Наслідок. Зовнішній кут трикутника більший за кожний внутрішній кут, не суміжний з ним.  ےABD > ےВАС,  ے𝐴𝐵𝐷 > ےАСВ.

VI. ЗАКРІПЛЕННЯ ВИВЧЕНОГО МАТЕРІАЛУ ЗАДАЧА 1. ЧИ ІСНУЄ ТРИКУТНИК З КУТАМИ:

1)    80° , 20°, 80°? (ТАК)

2)    80°, 30° І 70° ? (ТАК)

3)    40° , 50° І 60°? (НІ)

4)    120° , 35° І 35°? (НІ)

5.    ЧОМУ ДОРІВНЮЮТЬ ГОСТРІ КУТИ РІВНОБЕДРЕНОГО ПРЯМОКУТНОГО

ТРИКУТНИКА?   (45°)

6.    ЧОМУ ДОРІВНЮЄ СУМА ГОСТРИХ КУТІВ ПРЯМОКУТНОГО ТРИКУТНИКА?   (90°)

7.    ЯК ЗНАЙТИ КУТ ПРИ ВЕРШИНІ РІВНОБЕДРЕНОГО ТРИКУТНИКА?В=180° - 2ꞏА    АБО    В=180° - (A+C)

8.    ЯК ЗНАЙТИ КУТ ПРИ ОСНОВІ РІВНОБЕДРЕНОГО ТРИКУТНИКА?

(A = С =( (180° - В) : 2)

ЗАДАЧА 2. ЗНАЙДІТЬ ТРЕТІЙ КУТ ТРИКУТНИКА АВС, ЯКЩО ДВА ЙОГО КУТИ ДОРІВНЮЮТЬ:

1)       ےА = 45°, ےB =36°; 2) ےА = 140°, ےB =20°.

РОЗВ’ЯЗАННЯ   ےА+ ےВ+ ےС=180° (ЗА ВЛАСТИВІСТЮ СУМИ КУТІВ ТРИКУТНИКА) 1)  ےС =180°- (45°+36°),   ےС=99°.

2)       ےС =180°- (140°+20°),   ےС=20°.

ВІДПОВІДЬ: 1) 99°; 2) 20°.

ЗАДАЧА 3. ДАНО ТРИКУТНИК АВС, АВ=ВС,  ےВ У 3 РАЗИ БІЛЬШИЙ, НІЖ  ےА. ЗНАЙДІТЬ КУТИ ТРИКУТНИКА.

Розв’язання.

                                                                       В   1) Нехай градусна міра  ےА=х°.  АВС – рівнобедрений,

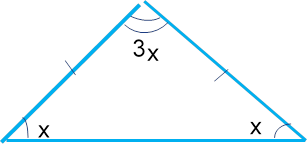бо АВ=ВС (за умовою), то  ےС =  ےА =х° (за властивістю кутів при основі рівнобедреного трикутника).  ےВ=(3х)° (за умовою).

2) Оскільки   ےА+ ےВ+ ےС=180 (за властивістю суми

                         ^{А                                                С}    кутів трикутника), то х+х+3х=180, 5х=180, х=36.  ےА

=  ےС =36°. ےВ=3х =3ꞏ36°= 108°.

Відповідь: 36°, 108°, 36°

Задача 4. Знайти кути трикутника, якщо вони пропорційні числам 2:3:7.

В ДАНО: ∆ АВС .  ےА:  ےВ: ےС = 2: 3: 7.

ЗНАЙТИ: ےА,  ےВ,  ےС.

РОЗВ’ЯЗАННЯ

У ∆ АВС  ےА+ ےВ+ ےС=180 (ЗА ВЛАСТИВІСТЮ СУМИ КУТІВ ТРИКУТНИКА). НЕХАЙ Х – КОЕФІЦІЄНТ ПРОПОРЦІЙНОСТІ,  ےА: ےВ: ےС=2:3:7. ТОДІ ГРАДУСНІ МІРИ КУТІВ

                _{А                                   С}  ВІДПОВІДНО ДОРІВНЮЮТЬ:  ےА= (2Х)°,  ےВ = (3Х)°,  ےС =

(7Х)°. МАЄМО РІВНЯННЯ: 2Х+3Х+7Х=180, 12Х=180, Х=180:12, Х=15. ےА=(2Х)° =2ꞏ15°=30°, ےВ=(3Х)° =3ꞏ15°=45°, ےС=(7Х)° =7ꞏ15°=105°.

ВІДПОВІДЬ:30° ,45° ,105°.

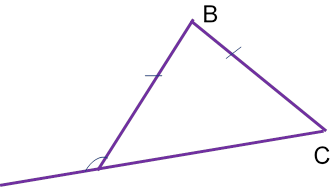
ЗАДАЧА 5 . ОБЧИСЛИТИ КУТИ ТРИКУТНИКА АВС, ЯКЩО АВ=ВС І ЗОВНІШНІЙ КУТ ВАD=140°.

Дано :  АВС, АВ=ВС, ےВАD=140° - зовнішній.

Знайти: ےВАС, ےАВС, ےАСВ.

Розв’язання.

 АВС, АВ=ВС (за умовою), то  АВС – рівнобедрений і

D             ^А  ےВАС = ےАСВ (за властивістю кутів при основі

рівнобедреного трикутника).

ےВАD + ےВАС =180° (за властивістю суміжних кутів). ےВАС =180° - ےВАD,  ےВАС =180° - 140° =40°,   ےАСВ=40

°.

ےВАD =  ےАВС +  ےАСВ (за властивістю зовнішнього кута).   ےАВС =140°- 40° =100°.

Але даний кут можна було визначити іншим способом, скориставшись властивістю суми кутів трикутника.

Відповідь: 40° , 100° , 40°.

ДОДАТКОВІ ЗАВДАННЯ:

1.                        ОДИН ІЗ ГОСТРИХ КУТІВ ПРЯМОКУТНОГО ТРИКУТНИКА У 5 РАЗІВ БІЛЬШИЙ, НІЖ ДРУГИЙ. ЗНАЙТИ ЦІ КУТИ.

2.                        ОДИН ІЗ КУТІВ ТРИКУТНИКА 60°. ЗНАЙТИ МІРИ ДВОХ ІНШИХ КУТІВ, ЯКЩО ДРУГИЙ БІЛЬШИЙ ВІД ТРЕТЬОГО НА 30°.

3.                        ЗНАЙДІТЬ  ТРЕТІЙ КУТ ТРИКУТНИКА, ЯКЩО  ДВА ЙОГО КУТИ ВІДПОВІДНО ДОРІВНЮЮТЬ 27° І 112° . 4.ОБЧИСЛИТИ КУТИ РІВНОБЕДРЕНОГО ПРЯМОКУТНОГО ТРИКУТНИКА. 5. ДВА КУТИ ТРИКУТНИКА РІВНІ ПО 60°. ДОВЕДІТЬ , ЩО ЦЕЙ ТРИКУТНИК РІВНОСТОРОННІЙ.

6. ЗНАЙДИ ЗОВНІШНІ КУТИ ТРИКУТНИКА, ЯКЩО ВІДОМІ ДВА ЙОГО ВНУТРІШНІ КУТИ: 25° І 73°.

VIІ.   ПІДСУМОК  УРОКУ.

СЬОГОДНІ  НА  УРОЦІ  МИ  ВІДКРИЛИ  ДОСЛІДНИМ  ШЛЯХОМ  ТЕОРЕМУ  ПРО 

СУМУ  КУТІВ  ТРИКУТНИКА  ,  ДОВЕЛИ  ТЕОРЕМУ,  НАВЧИЛИСЬ 

ЗАСТОСОВУВАТИ  НАБУТІ  ЗНАННЯ  В  ПРАКТИЧНІЙ  ДІЯЛЬНОСТІ.  МИ  ЩЕ  РАЗ 

ПЕРЕКОНАЛИСЯ ,  ЩО  ГЕОМЕТРІЯ  ЦЕ  НАУКА ,  ЯКА  ВИНИКЛА  З  ПОТРЕБ 

ЛЮДИНИ.  АДЖЕ,  ЯК  ПИСАВ  ГАЛІЛЕЙ: ”ПРИРОДА  РОЗМОВЛЯЄ МОВОЮ  МАТЕМАТИКИ :  БУКВИ  ЦІЄЇ  МОВИ - КОЛА , ТРИКУТНИК  ТА  ІНШІ  ГЕОМЕТРИЧНІ  ФІГУРИ”. VIІІ. ДОМАШНЄ  ЗАВДАННЯ.

ВИВЧИТИ П. 16. РОЗВ’ЯЗАТИ  ЗАДАЧІ : №359, №366.

ЗАДАЧА. ЗНАЙДИ КУТИ РІВНОБЕДРЕНОГО ТРИКУТНИКА, ЯКЩО ЗОВНІШНІЙ КУТ ПРИ ОСНОВІ ДОРІВНЮЄ 116°.

БАЖАЮ УСПІХІВ!