Презентація. Узагальнення знань із теми: "Паралельність прямих і площин у просторі"

Мета: узагальнити і систематизувати знання учнів. Відпрацювати навички учнів застосовувати властивості  паралельності прямих та площин до   розв’язування вправ та побудови перерезів многокутників. Розвивати пізнавальну діяльність учнів. Виховувати математичну культуру та інтерес до геометрії.

«Недостатньо мати лише добрий розум, головне – це раціонально застосовувати його».   (Р. Декарт)

Хід уроку

I. Перевірка домашнього завдання (обмін зошитами).

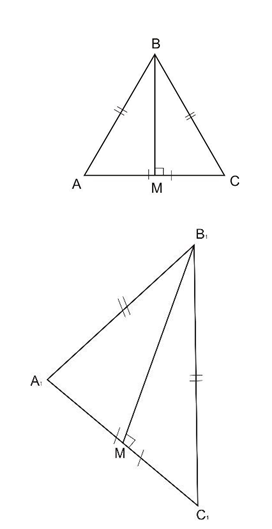Задача 1. Побудувати проекцію рівнобедреного трикутника АВС (АВ=ВС). Побудувати проекцію висоти трикутника, проведеної з вершини В.

Оскільки ∆ АВС – рівнобедрений, то зображенням висоти ВМ є зображення медіани і бісектриси  ∆А1В1С1.

Побудова.

1.       ∆ А₁В₁С₁ (А₁В₁=В₁С₁);

2.       А₁М₁=М₁С₁;

3.       В₁М₁-висота (за властивість медіани рівнобедреного трикутника).

Задача №2. Побудувати проекцію рівнобічної трапеції АВСD та її висоти , опущеної з вершини В.

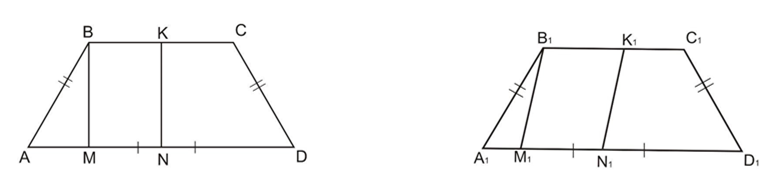
А₁В₁С₁D₁ – проекція трапеції АВСD A1D1||B1C1, A1B1=C1D1

K₁N₁ – вісь симетрії.

Побудова.

1.    А₁В₁С₁D₁ – трапеція, ( А₁𝐷₁|| В₁С₁)

2.    B1K1=K1C1,  A1N1=N1D1

K1N1  A1D1,

B1M1  A1D1,B1M1|| K1N1

B₁M₁ i K₁N₁ – зображення висот.

II. Актуалізація опорних знань учнів (обмін

зошитами)

I       Варіант

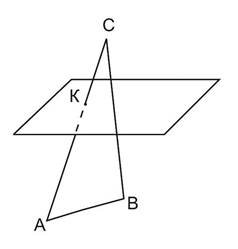
Через точку К сторони АС трикутника АВС проведена площина α,| паралельна прямій АВ.

а) Як розташовані прямі АВ і КМ (М – точка перетину прямої ВС і площини α)?

б) Обчислити довжину відрізка КМ, якщо АК=4 см, КС=6 см, АВ=5 см.

II   варіант

Через точку К сторони АС трикутника АВС проведена площина α, паралельна прямій АВ.

а) Побудувати точку перетину площини і сторони ВС (точку М).

б) обчислити довжину відрізка КМ, якщо КМ+АВ=26 см, СК:КА=4:5.

III. Тренувальні вправи

(Робота в парах. Учні отримують завдання та картки для виставлення балів)

Задача 1 (I,  II ряд).

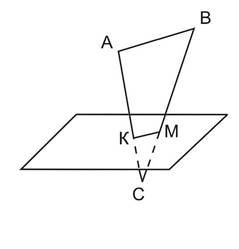
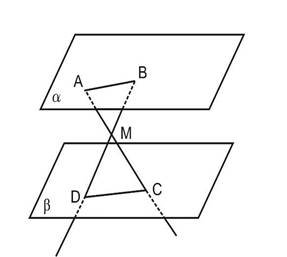
•             Точки А і В розміщені в одній з паралельних площин, С і D – в другій.

Відрізки BD і AC перетинаються в точці М; BD = 15 см, АВ = 4 см, DC = 6 см.

б) обчислити довжину відрізка DM.

Задача 2 (III ряд).

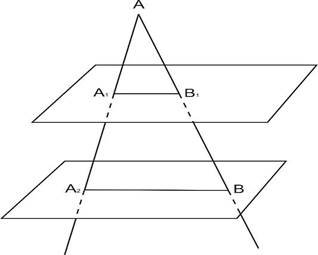
•             Два промені з початком в точці А перетинають одну з паралельних площин в точках А_1,В₁, а другу в точках А₂ , В₂.

а) як розміщені прямі  А₁В₁ і А₂В₂;   

б) обчислити А В₁, якщо А₁ = 4 см, А₂В₂= 16 см, В₁В₂ = 15 см .

Дано: 𝛼 ∥ 𝛽, A і B ∈ 𝛼, D і C ∈ 𝛽, АC     BD=M,  AC     BD= γ,

𝛼 ∩ γ = АВ – лінія перетину двох площин.

𝛽 ∩ 𝛾 = DC лінія перетину площин. AB || DC (як лінії перетину паралельних площин перетнутих третьою). Задача зводиться до

=             планіметричної.

= ∆ABM~ ∆MDC, бо  ےAMB= ے

DMC, як вертикальні,

k=; BM=BD-DM;

BM= 15-DM;

𝐵𝑀∗𝐷𝐶

DM=;    DM= 

𝐴𝐵

2 DM=45-3 DM; 2 DM+3 DM=45; 5 DM=45; DM=9 см. DM=9 см.

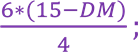
Відповідь: 9 см.

Дано: 𝛼 ∥ 𝛽, АА₂ ∩АВ₂= А,

АА2     ∩ АВ2= 𝛾 , А₁,В₁ ∈ 𝛼 , А₂, В₂ ∈ 𝛽, .

𝛼 ∩ 𝛾 =А₁В₁-лінія перетину площин

𝛽 ∩ 𝛾 =А₂В₂-лінія перетину площин           А₁В₁|| А₂В₂(як лінії перетину паралельних площин перетнутих третьою).

Задача зводиться до планіметричної.

∆ AA₁B₁~ ∆AA₂B₂ (за спільним гострим кутом А).

k =,

AB

вимірювання відрізків),

AB₂=AВ₁+15;

,

4 AB₁=AB₁+15; 3AB₁=15; AB₁=5 см.

Відповідь: 5 см.

Цікаво знати

•                         Як далеко ” за сім верст  ”

1 верста =1.08км.7 верст=1.08*7=7.56 км.

•                         Про дуже розумну людину кажуть “ семь пядей во лбу ” .

Чи існує людина, яка має таке число?

1пядь= 18см;7пядей=18*7=126 см.

•                         Припустимо, що ви обійшли земну кулю пішки. На скільки довший шлях пройшла ваша голова ніж ноги, якщо ваш зріст,наприклад180 см?

Приблизно на 11м.

Задача №3.

Побудувати переріз куба ABCDA₁B₁C₁D₁ площиною, яка проходить через вершини А, С і точку К, взяту на ребрі А₁В₁. Встановити вид перерізу.

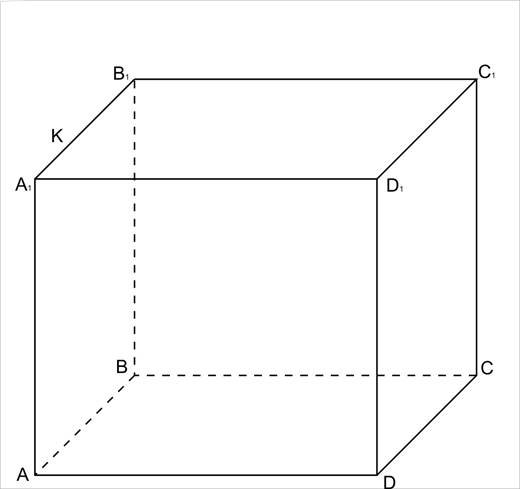
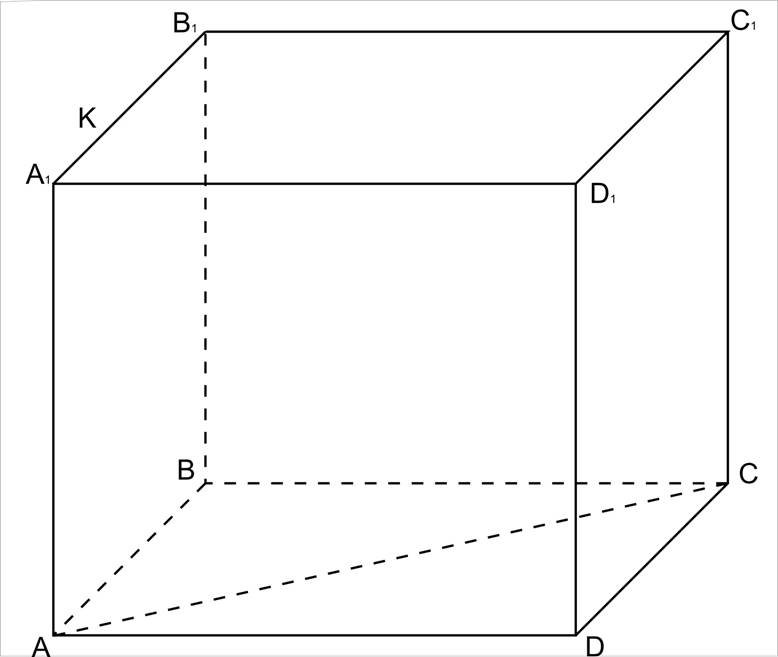
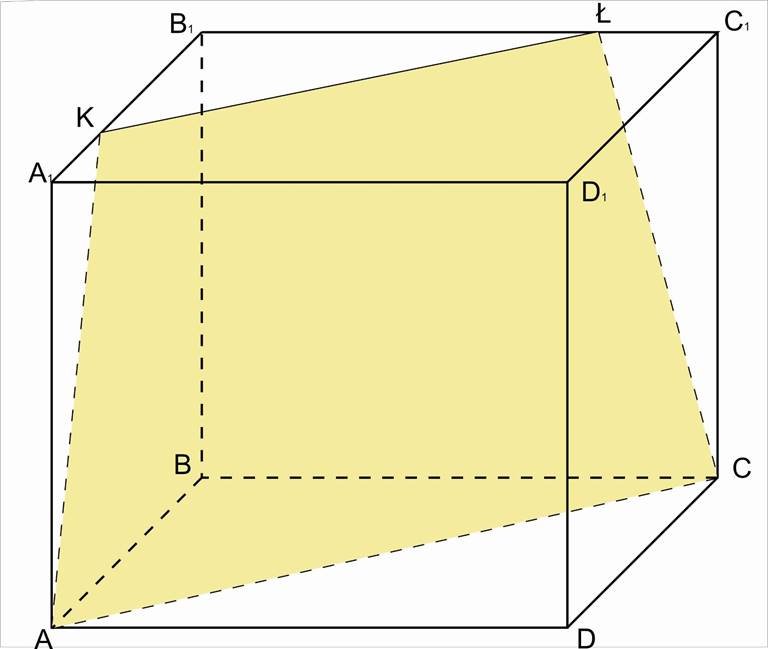
Розв’язання..

1.    α    I(ABCD) = АС (А і С є α за умовою) – лінія перетину.

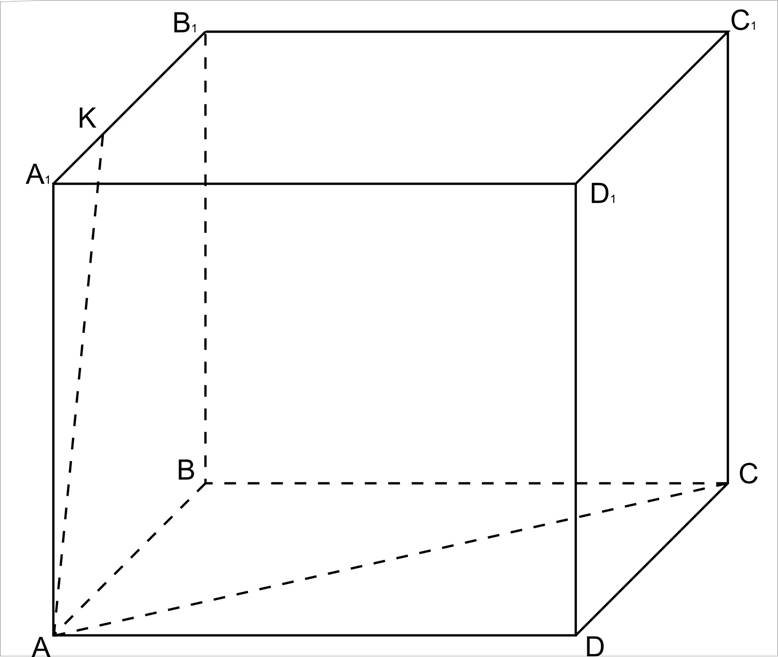
2.    А і К є (АА₁В₁В),

(АА₁В₁В)    α = АК.I

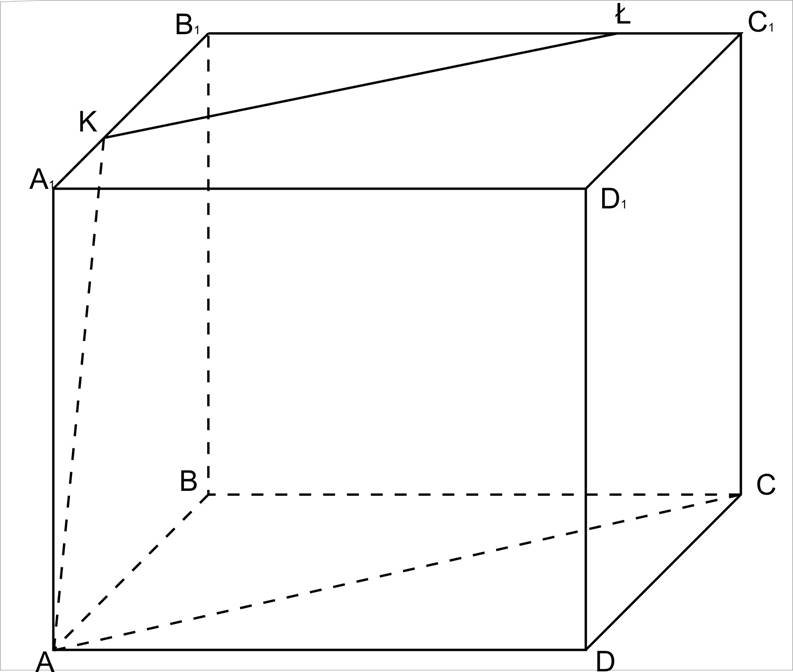
3.    К і АС є α, α     I(A₁B₁C₁D₁)=КŁ, КŁ || AC (за властивістю паралельних площин).

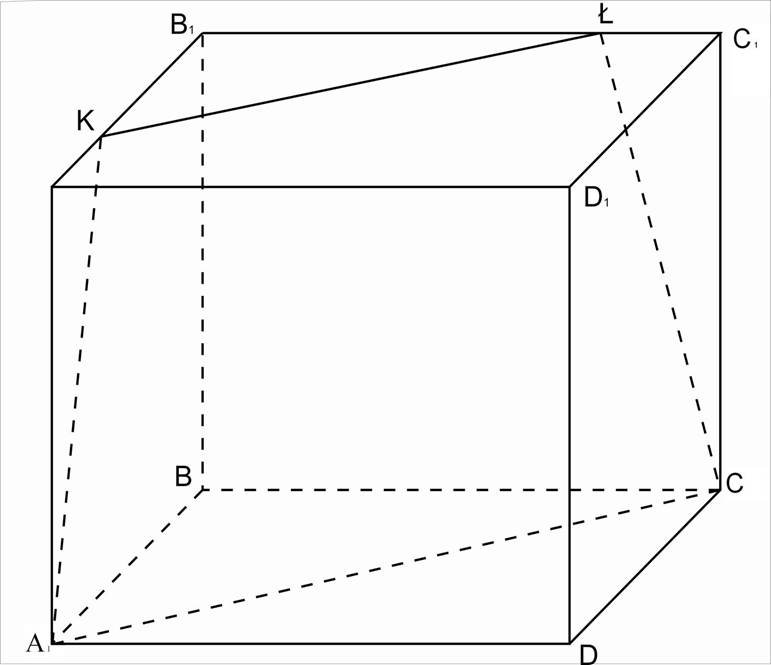
4.    α I(DD₁СС₁)= ŁС.

AKŁC – трапеція, бо АС ||KŁ.

Задача №4

Побудувати переріз прямокутного паралелепіпеду ABCDA₁B₁C₁D₁ площиною α, яка проходить через вершини А, С і внутрішню точку М ребра А₁D₁ .

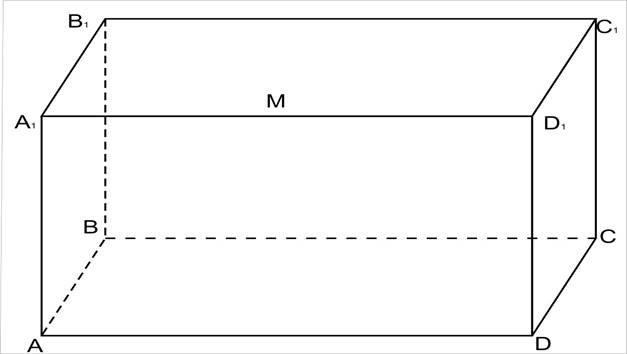
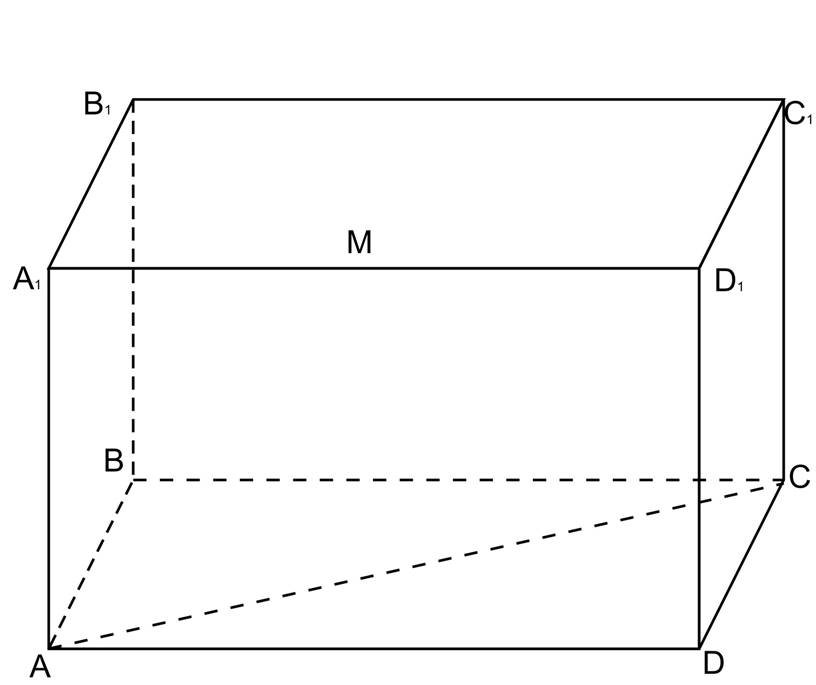
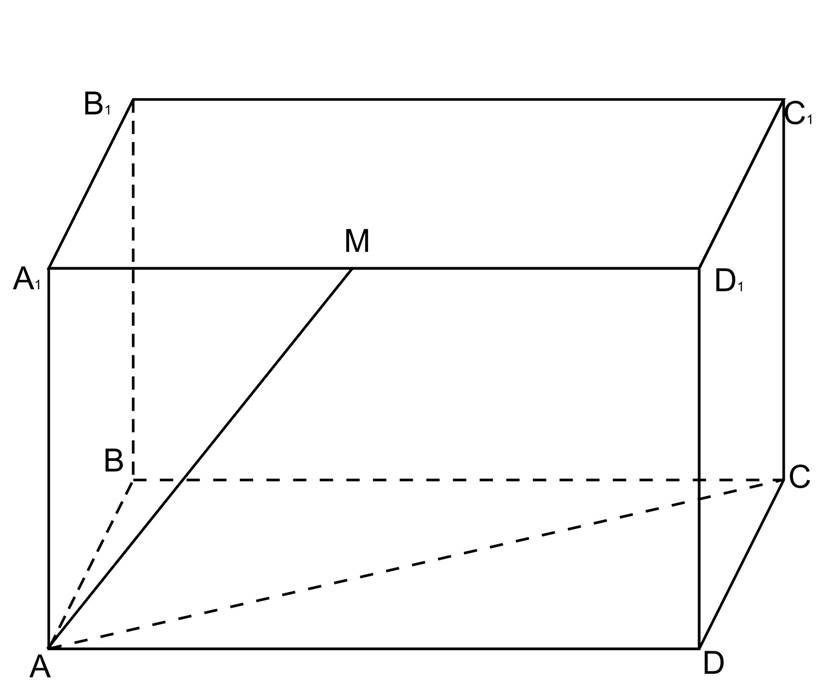
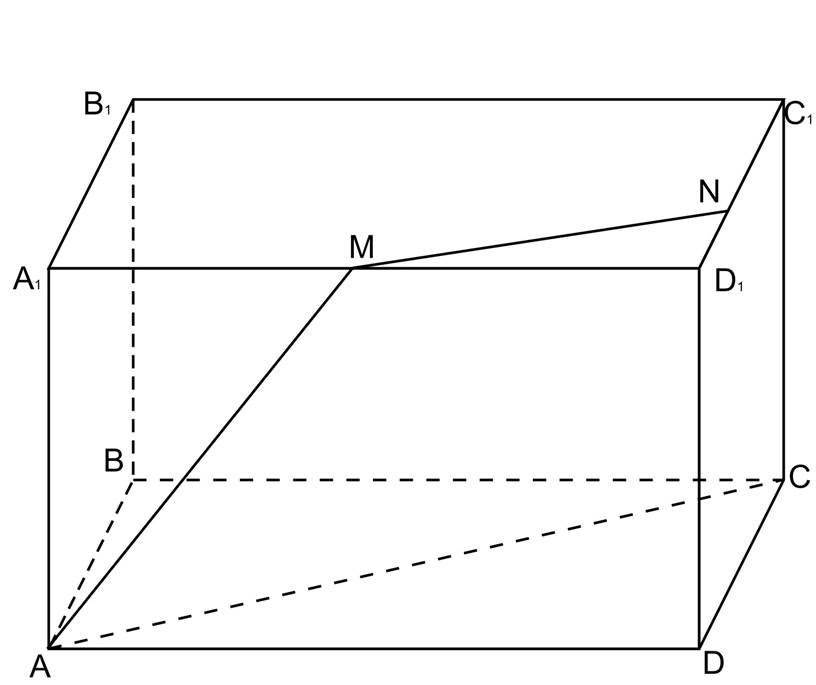
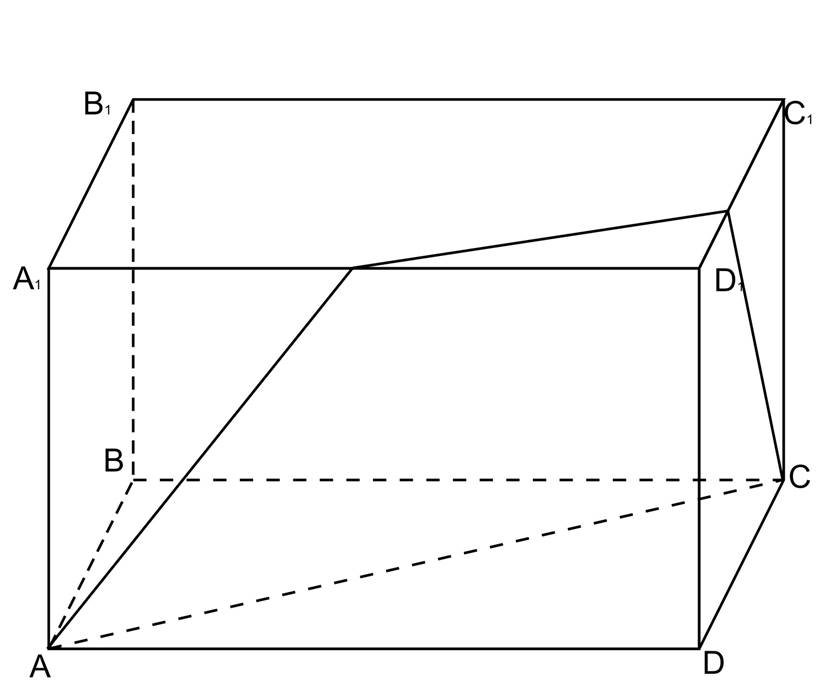
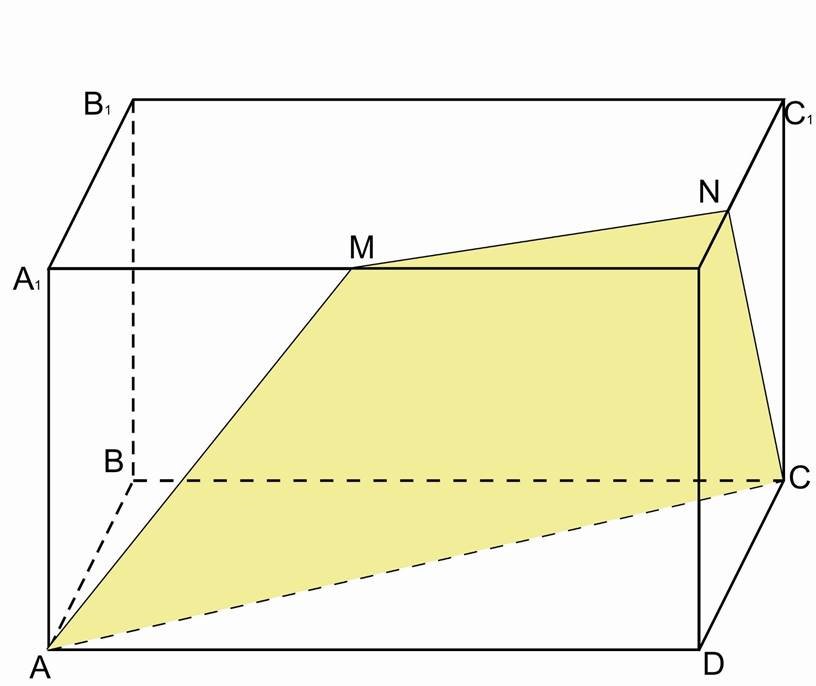
Розв’язання.

1.    Проведемо АС, бо А і С є (ABCD).

2.    А, М є (АА₁DD₁ ), то α  ^I(АА₁DD₁ ) = АМ.

3.    АС і М є α, то проводимо MN||AC (за  властивістю паралельних площин ).

(A₁B₁C₁D₁ )   Iα = MN.

4.    N, C є (DD₁C₁C), то α I (DD₁CC₁)=NC .

AMNC – шуканий переріз.

Oскільки, AC || MN, то AMNC – трапеція.

Задача №5.

Побудуйте переріз куба площиною, яка проходить через точки М, К, Р, якщо:

а) К є DD₁, P є СС₁, М співпадає з В₁ (Домашнє завдання);

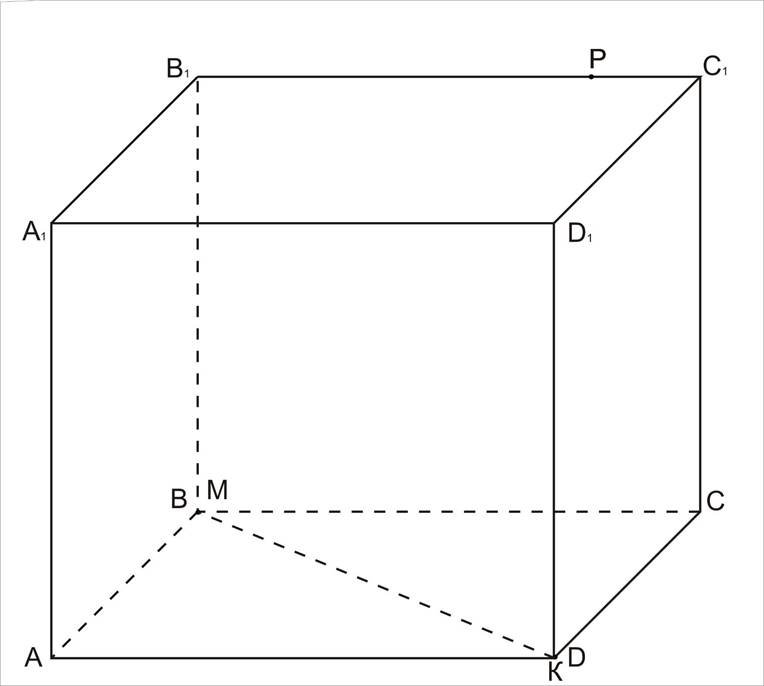
б) М співпадає з В, К співпадає з D, Р є В₁С₁.

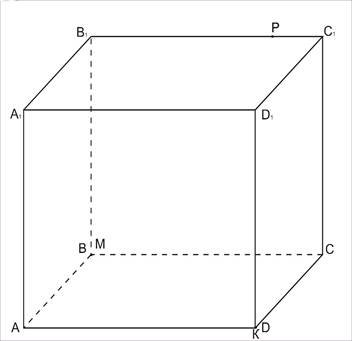
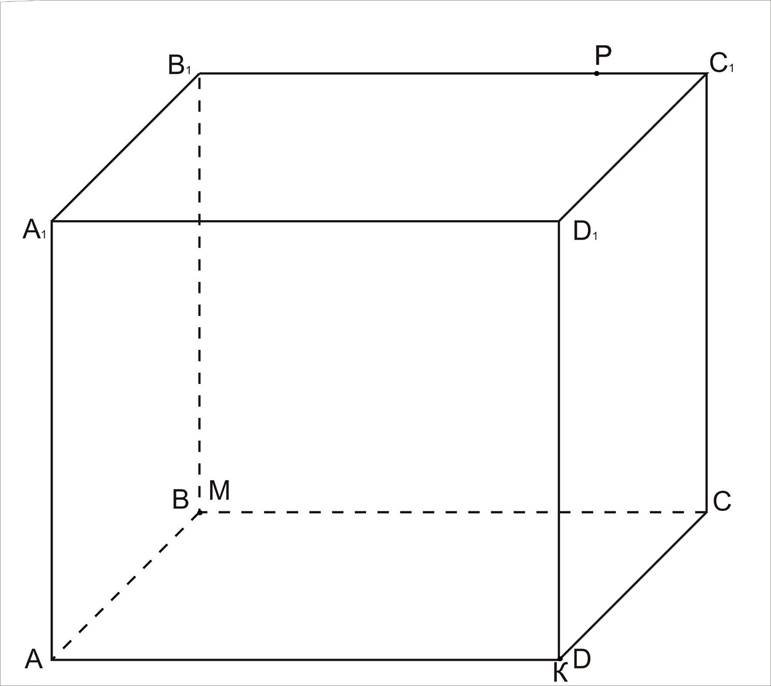
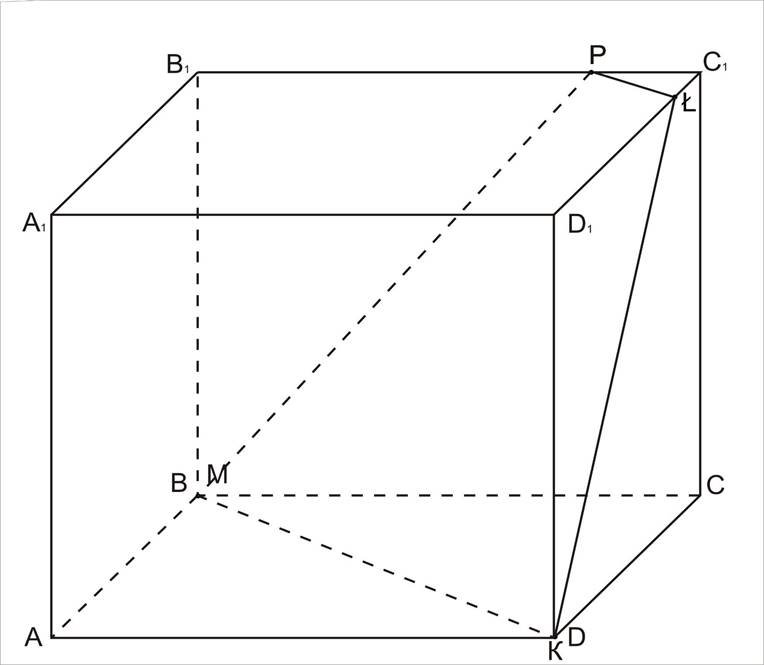
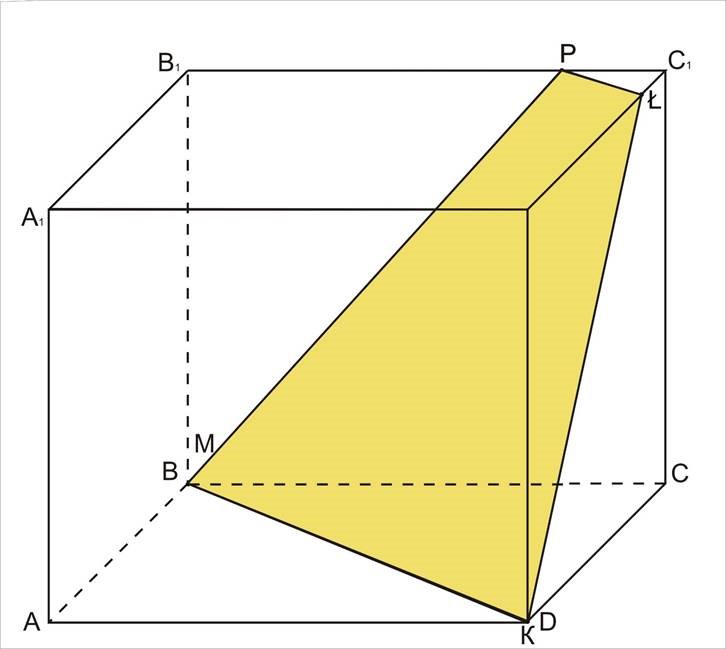
Розв’язання.

1.     α (ABCD) = MK;

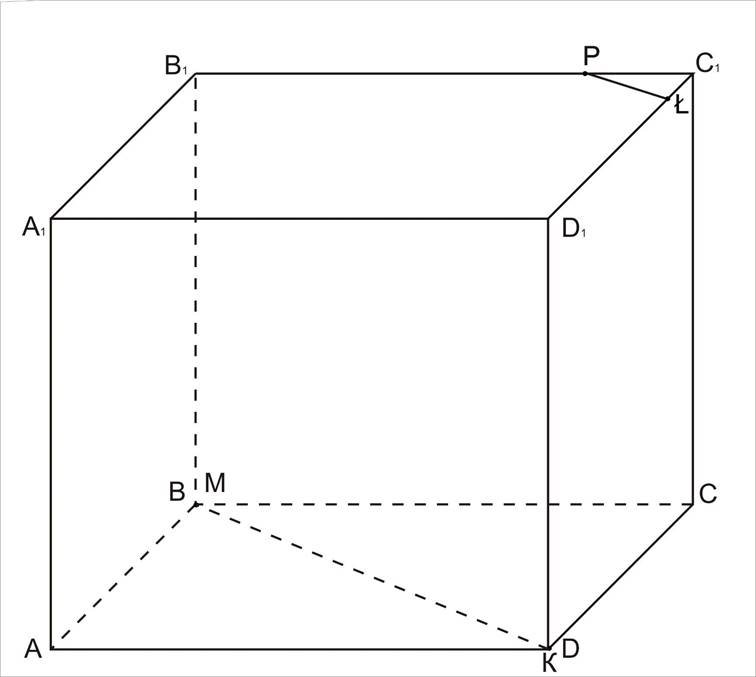
2.     Р є α, МК є α, то α      ( А₁B₁С₁D₁ )= PŁ – лінія перетину.

PŁ||MK (за  властивістю  паралельних площин),

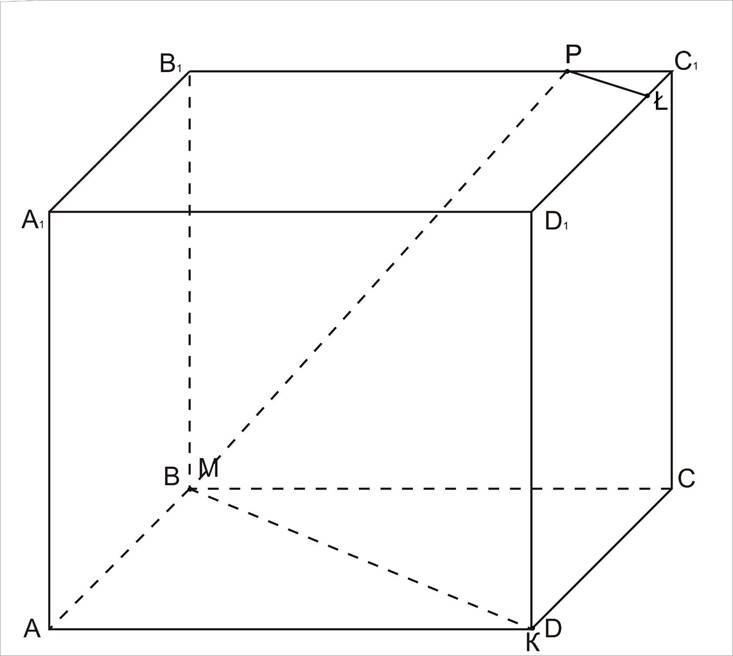
3.     α      ( ВВ₁СС₁ )= МР;

4.     α    ( D₁DCC₁) = KŁ.

MKŁP – шуканий переріз.

IV. Домашнє завдання:  №37 (а), №5 (а). V. Підсумок уроку.

Зібрати картки. Виставити бали .

Дякую !