Презентація: "Світ тригонометрії"





























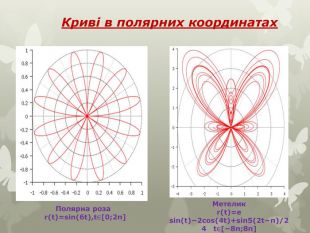
![Полярна роза r(t)=sin(6t),t∈[0;2π] Метеликr(t)=e sin(t)−2cos(4t)+sin5(2t−π)/24 t∈[−8π;8π] Криві в полярних координатах Полярна роза r(t)=sin(6t),t∈[0;2π] Метеликr(t)=e sin(t)−2cos(4t)+sin5(2t−π)/24 t∈[−8π;8π] Криві в полярних координатах](/uploads/files/374096/98657/105179_images/36.jpg)






Мета моєї роботи: дослідити історію розвитку тригонометрії і перспективу багатогранності її застосування, графічні можливості тригонометричних функцій. Завдання: Простежити походження тригонометрії, символів і термінів, розглянути шлях розвитку тригонометрії. Розглянути можливості застосування тригонометрії в реальному житті. Розкрити на конкретних прикладах можливості використання тригонометричних функцій, що дозволяють "мало цікаві" функції перетворювати на функції, графіки яких мають дуже оригінальний вигляд. Гіпотеза: Тригонометрія дуже важлива і цікава. Більшість фізичних явищ природи, фізіологічний процесів, закономірностей в музиці і мистецтві можна описати за допомогою тригонометрії і тригонометричних функцій.
Одним з основоположників тригонометрії вважають старогрецького астронома Гіппарха, що жив в II ст. до н. е. Саме йому приписують створення тригонометрії як науки, пограничної між геометрією і астрономією. Гіппарх уперше розглянув тригонометричне коло і обчислив таблицю хорд у крузі, що стало основним елементом грецької тригонометрії на площиніГІППАРХ НІКЕЯ
Насір ад-Дін Мухаммад ат-Тусі Велика заслуга у формуванні тригонометрії як окремої науки належить азербайджанському ученому Насір ад-Діну Мухаммаду ат-Тусі що написав "Трактат про повний чотирикутник", в якому містяться практичні способи рішення типових завдань, у тому числі важких, вирішених самим ат-Тусі - наприклад, побудова сторін сферичного трикутника по заданих трьох кутах. Насір ад-Дін Мухаммад ат-Тусі (1201-1274)
Німецький вчений Йоганн Мюллер, відомий в науці під ім'ям Регіомонтан, видав працю "П'ять книг про трикутники усіх видів", що зіграла важливу роль в розвитку тригонометрії. У ній дано систематичний виклад тригонометрії як самостійної наукової дисципліни. Він узагальнює методи рішення прямокутних трикутників і дав таблиці синусів з точністю до 0,0000001. РЕГІОМОНТАНРегіомонтан (1818—1899)
Багато європейських математиків працювали в області тригонометрії. Серед них такі великі учені, як Микола Коперник (1473-1543), Тихо Бразі (1546-1601) , Йоганн Кеплер (1571-1630)і Франсуа Вієт (1540-1603). Микола Коперник(1473-1543)Тихо Бразі(1546-1601) Йоганн Кеплер(1571-1630)Франсуа Вієт(1540-1603)Європейські математики і тригонометрія
Франсуа Вієт (1540-1603 р.)Франсуа Вієт Франсуа Вієт (1540-1603) доповнив і систематизував різні випадки рішення плоских і сферичних трикутників, відкрив "плоску" теорему косинусів і формули для тригонометричних функцій кратних кутів. Ісаак Ньютон (1643-1727р.)Ісаак Ньютонрозклав функції в ряди і відкрив шлях для їх використання в математичному аналізі Європейські математики і тригонометрія
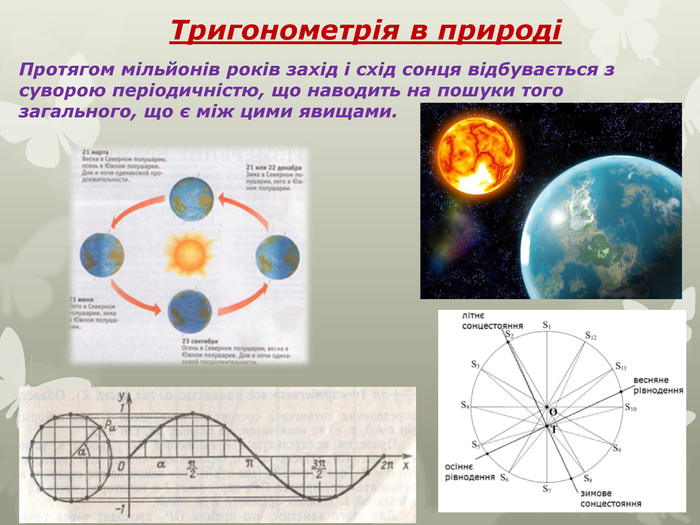
Тригонометрія знаходить велике застосування в механіці, фізиці і техніці, особливо при вивченні коливальних рухів і інших періодичних процесів. Скрізь, де доводиться мати справу з періодичними процесами і коливаннями, знайшли застосування тригонометричні функції. Тригонометрія в науках
Тригонометрія у фізиціУ техніці і навколишньому світі часто доводиться стикатися з періодичними (або майже періодичними) процесами, які повторюються через однакові проміжки часу. Такі процеси називають коливальними. Існують різні види коливальних явищ, наприклад: механічні коливання, гармонійні коливання. Вивчення коливання всякого роду важливе. Вже хоча б тому, що з коливальними рухами або хвилями ми стикаємося дуже часто в середовищі, що оточує нас, і з великим успіхом використовуємо їх
Тригонометрія у хіміїПеріодичний закон Д. И. Менделєєва - одно з найбільших відкриттів закону періодичності властивостей хімічних елементів і утворюваних ними хімічних сполук від атомної маси і заряду ядра атома. Тут ми спостерігаємо періодичне змінення - послаблення металевих властивостей, перехід в неметалічні властивості, їх посилення, і період закінчується інертним газом. Дмитро Іва́нович Менделе́єв(1834 -- 1907 )
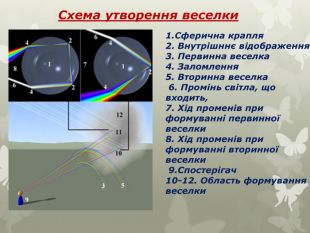
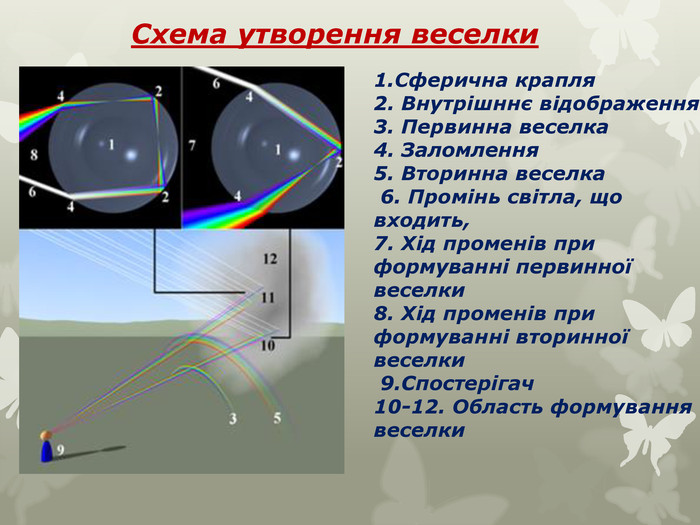
Світло і тригонометрія Заломлення світла — це зміна напрямку променя на межі двох середовищами різної щільності. Виявилося, що найпростіші тригонометричні формули і знання синуса кута падіння і кута заломлення дають можливість дізнатися постійний коефіцієнт заломлення для переходу світлового променя з однго конкретного середовища в інше.
1. Сферична крапля 2. Внутрішннє відображення3. Первинна веселка 4. Заломлення 5. Вторинна веселка 6. Промінь світла, що входить, 7. Хід променів при формуванні первинної веселки 8. Хід променів при формуванні вторинної веселки 9. Спостерігач 10-12. Область формування веселки. Схема утворення веселки
Північне сяйво Серед численних і приголомшливих явищ природи існує одне, справді унікальне, це північне сяйво. Для того щоб зрозуміти суть цього незвичайного явища, потрібно звернутися до фізики. Північне сяйво -- проникнення у верхні шари атмосфери планет заряджених часток сонячного вітру визначається взаємодією магнітного поля планети з сонячним світлом.
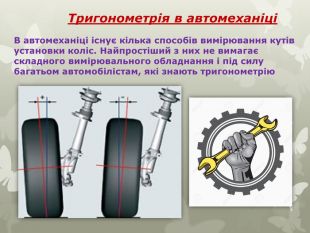
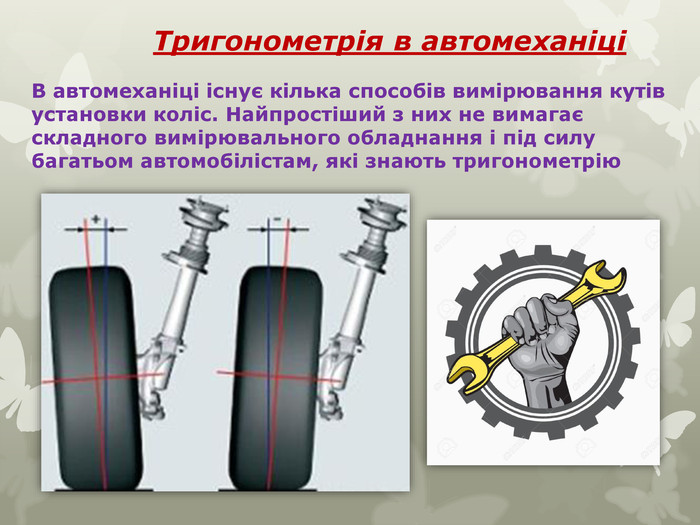
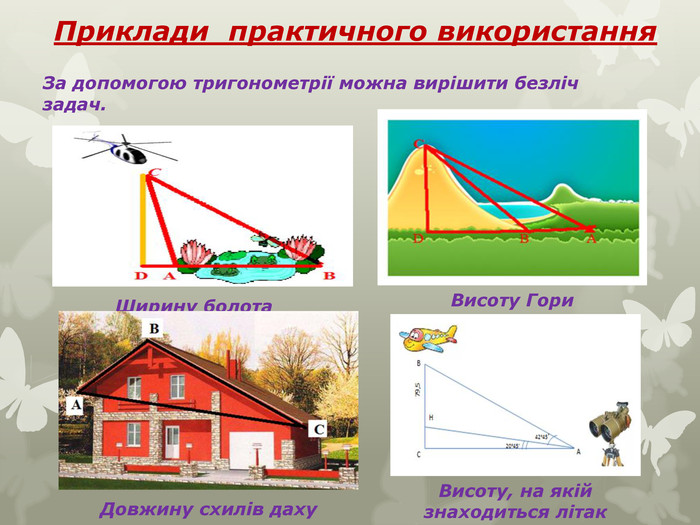
Багатофункціональна тригонометрія. Тригонометрія допомагає нашому мозку визначати відстань до об’єктів. Американські учені стверджують, що мозок оцінює відстань до об'єктів, вимірюючи кут між площиною землі і площиною зору. Ще художники Стародавнього Китаю малювали віддалені об'єкти вище поля зору, нехтуючи законами перспективи
Тригонометрія в мистецтві і архітектуріАрхітектура не єдина сфера науки, в якій використовуються тригонометричні формули. Більшість композиційних рішень і побудов малюнків проходило саме за допомогою тригонометрії. Культові будівлі в усьому світі були спроектовані завдяки математиці, яка може вважатися генієм архітектури. Антоніо Гауді - іспанський архітектор, більшість химерно-фантастичних робіт якого зведені у Барселоні.
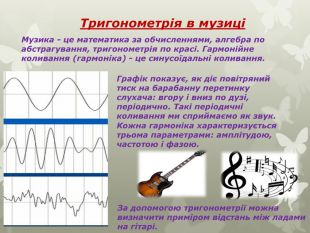
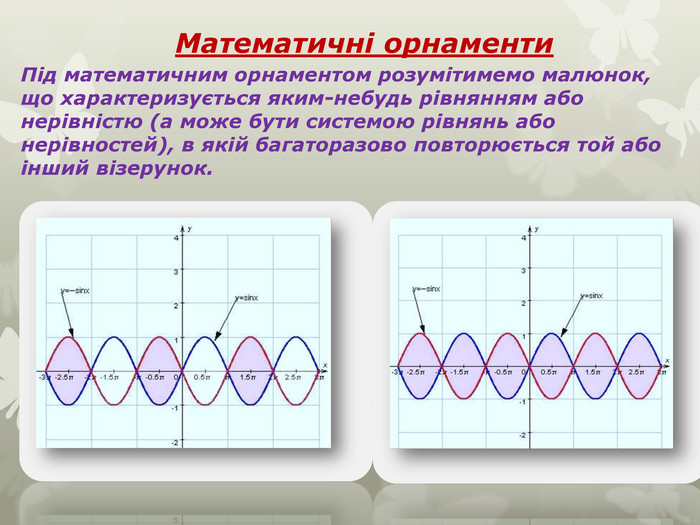
Тригонометрія в музиціМузика - це математика за обчисленнями, алгебра по абстрагування, тригонометрія по красі. Гармонійне коливання (гармоніка) - це синусоїдальні коливання. Графік показує, як діє повітряний тиск на барабанну перетинку слухача: вгору і вниз по дузі, періодично. Такі періодичні коливання ми сприймаємо як звук. Кожна гармоніка характеризується трьома параметрами: амплітудою, частотою і фазою. За допомогою тригонометрії можна визначити приміром відстань між ладами на гітарі.
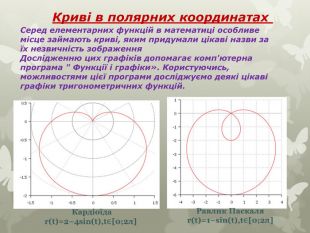
Полярні координати. При рішенні багатьох завдань зручніше користуватися так званими полярними координатами: на площині вибирають нерухому точку О (полюс) і промінь ОМ, що виходить з неї (полярна вісь). Положення точки М в цьому випадку визначається двома числами: її відстанню r від полюса і кутом = ∟РОМ . Числа r (полярний радіус) і (полярний кут) називаються полярними координатами точки М.
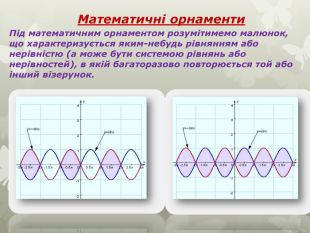
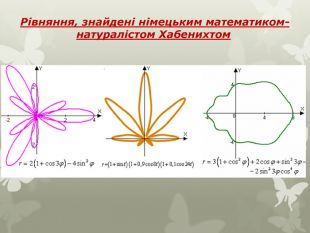
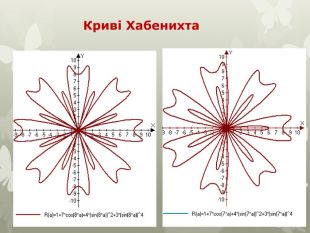
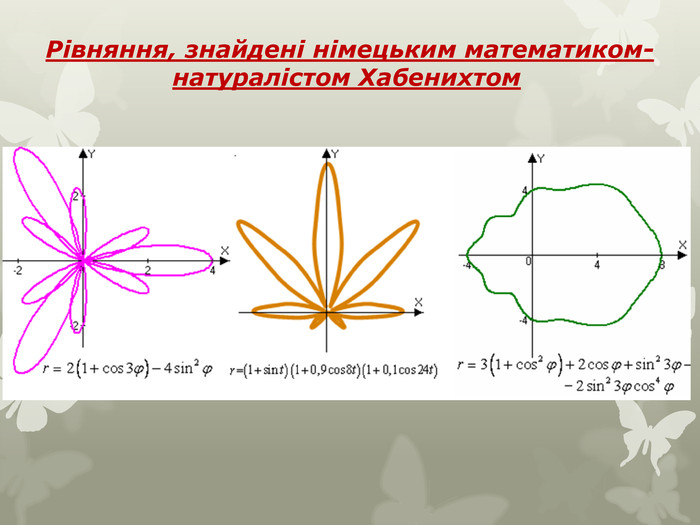
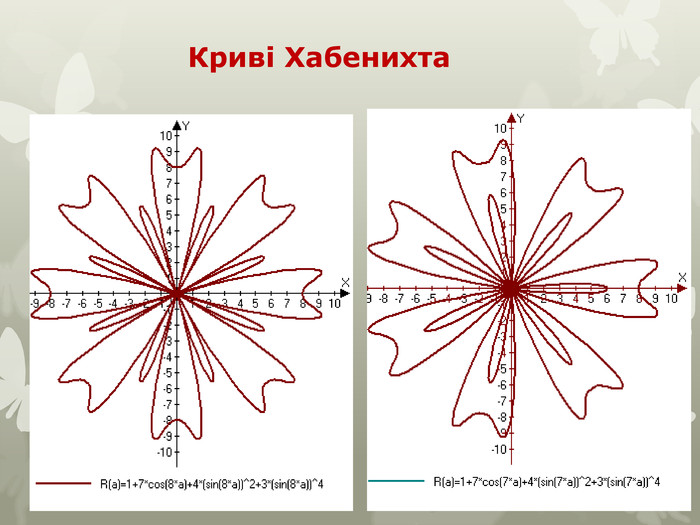
Серед елементарних функцій в математиці особливе місце займають криві, яким придумали цікаві назви за їх незвичність зображення. Дослідженню цих графіків допомагає комп'ютерна програма " Функції і графіки». Користуючись, можливостями цієї програми досліджуємо деякі цікаві графіки тригонометричних функцій. Криві в полярних координатах
Бджоли використовують полярні координати для обміну інформацією про джерела їжі. Знайшовши нове джерело їжі, бджола-розвідниця повертається у вулик і виконує танець, на мові якого розповідає, де знаходиться клумба. Причому усе це схоже на двохпелюсткову троянду. Таким чином, бджола-розвідниця повідомляє іншим бджолам полярні координати нового джерела їжі. Полярні координати у бджіл
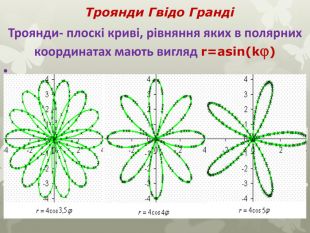
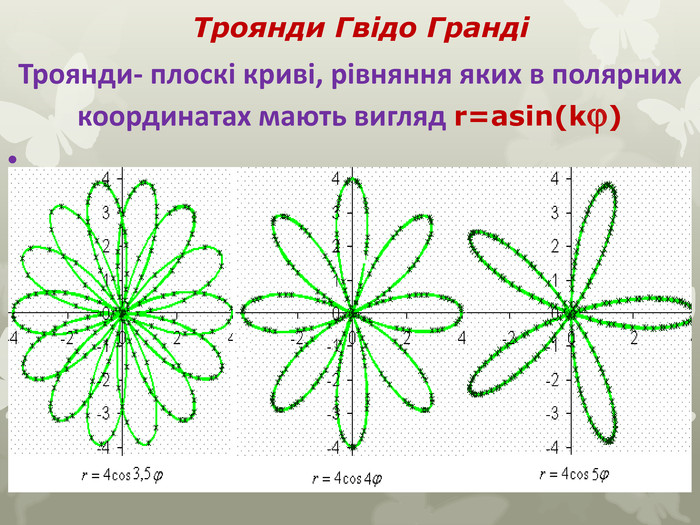
Якщо модуль k - раціональне число, то троянда складається з m пелюсток у разі, коли обидва числа m і n непарні, і з 2m пелюсток, якщо одно з цих чисел є парним. При цьому, на відміну від першого випадку кожна наступна пелюстка частково перекриватиме попередню3. Якщо модуль k - ірраціональне число, то троянда складається з незліченної безлічі пелюсток, що частково накладаються один на одного. Троянди Гвідо Гранді
ВИСНОВОК Ми привели лише малу частину того, де можна зустріти тригонометричні функції, з'ясували, що тригонометрія була викликана до життя необхідністю робити виміри кутів, але з часом розвинулася і в науку про тригонометричні функції. Довели, що тригонометрія тісно пов'язана з фізикою, зустрічається в природі, музиці, астрономії, медицині та в багатьох інших галуззях. Тригонометрія знайшла відображення в нашому житті, і сфери, в яких вона відіграє важливу роль, розширюватимуться. Використання моделюючої програми " Функції і графіки" дозволило досліджувати цікаві математичні криві, що задаються за допомогою тригонометричних рівнянь і побудовою графіків в полярних координатах.
-
 Новомлинська Дар'я Сергіївна 06.11.2022 в 19:06Загальна:5.0Структурованість5.0Оригінальність викладу5.0Відповідність темі5.0
Новомлинська Дар'я Сергіївна 06.11.2022 в 19:06Загальна:5.0Структурованість5.0Оригінальність викладу5.0Відповідність темі5.0


про публікацію авторської розробки
Додати розробку