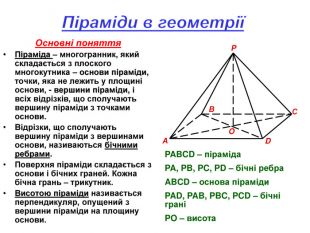
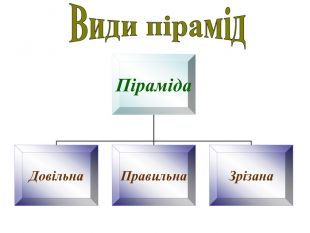
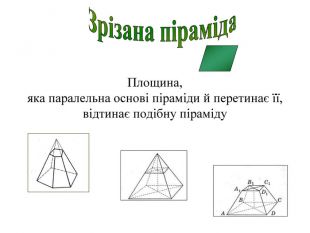
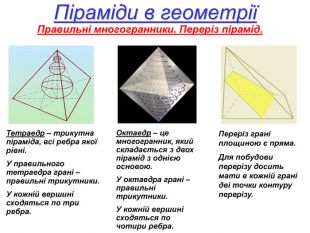
Методична розробка уроку на тему: "Піраміда"

Девіз уроку: “Знання можуть бути купою каміння, що задавила особистість. І знання можуть бути вершиною піраміди, на якій стоїть особистість.” М.Розов

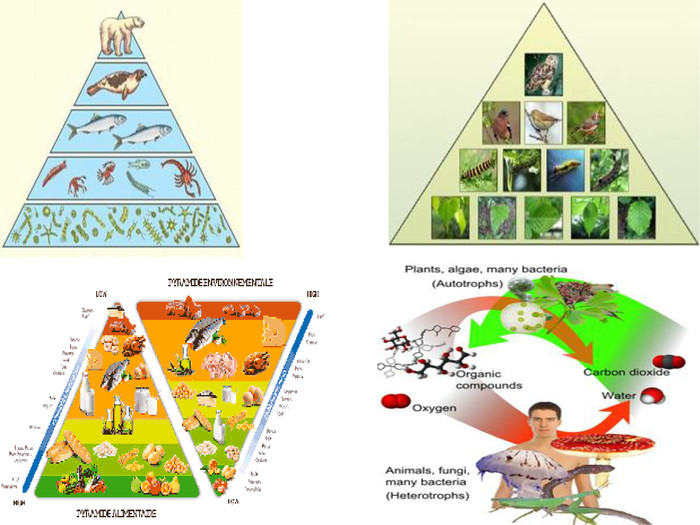
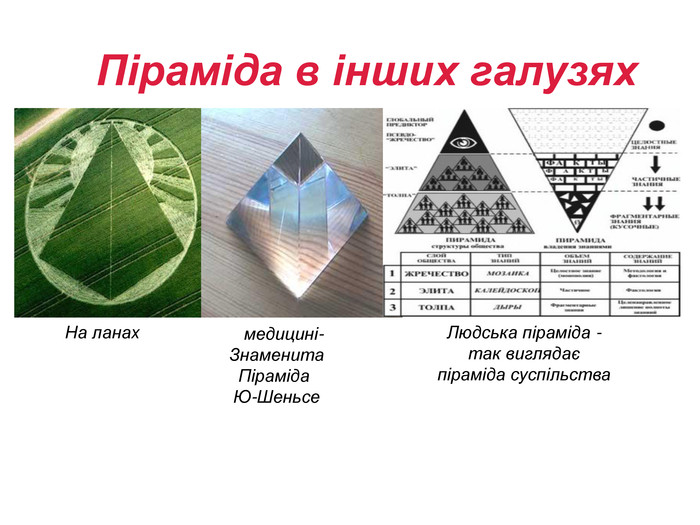
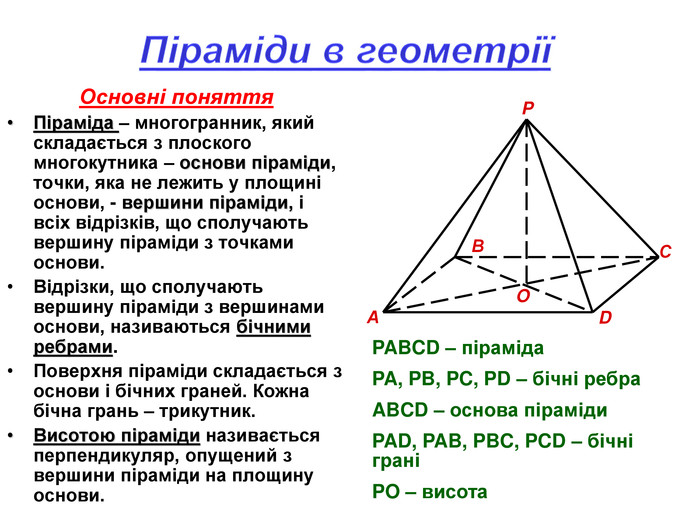
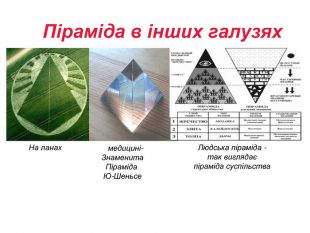
Мета уроку: Познайомити учнів з поняттям “ піраміда ”, її елементами. Розширити знання відомостями з історії, використанням властивостей пірамід в архітектурі, медицині, сільському господарстві

Ну що там храм прадавній Артеміди, Колос Родоський, це якісь дива! Дивіться: це фігура – піраміда, Краса її завжди, завжди жива. Нахилені до купи грані Вершину творять горду і стрімку. Усе довершене у ній прегарній, Хіба забути нам таку?

Історія пірамід Пірамідами називають гробниці древнєєгипетських фараонів Древнього та Середнього царств, втілюючі ідею про надлюдську велич правителя. Найбільша піраміда Хеопса в Гізі (висота146,6м, 28 в. до н.е.).продавніші піраміди фараона Джосера в Саккара і фараона Снофру в Медумі (ІІІ тис.до н.е.)

Піраміда в Гізі – одна із самих відомих споруд на Землі. Це одне із семи древніх чудес світу, яке дійшло до наших днів. Її вік сягає 4 600 – 4 800 років. Вражають розміри: Висота – 146 м, Довжина сторони основи – 230 м, Загальна площа – більше 5 га. Вона складена із 2,5 мільйонів кам'яних блоків, які з високою точністю підігнані один до одного.

На цій піраміді ще й досі збереглися сліди від насипів, по яким тягли блоки.

Тайна пірамід і досі не розгадана. Науковці, які намагались з’ясувати, яким чином древні будівники змогли побудувати ці грандіозні споруди (і не просто побудувати, а придати їм геометрично правильну форму), просто заходили у глухий кут.

Піраміда широко використо-вується в архітектурі

Піраміди в архитектурі Піраміда в Каракасі Піраміда у Франції Піраміда рівноваги Піраміда- крамниця Парк часу в Свердловську

Піраміди у фізиці Історична цінність пірамід – наявність великої кількості енергії, створеної завдяки правильності форми пірамід. Створювані поля у середині пірамід дозволяють нейтралізувати негативну енергію і перетворити її в позитивну. Єдина система пірамід на планеті координує процес перетворення енергії у просторі і у часі.

Піраміди виконують також роль стабілізатора параметрів у русі планети. Важною умовою при енергоінформаційному обміні Космос-Земля-Космос є утримання планети на постійній орбіті з постійним кутом нахилу земної осі до Сонця і, звичайно ж, стала швидкість обертання навколо Сонця і своєї осі. Щоб зберегти ці параметри, треба постійно вводити стабілізаційну програму в ядро і плазму Землі.

Найбільш приголомшеними знахідками минулого століття стали дані НАСА. У 1976 р. американський космічний апарат “Вікінг”, облітаючи Марс, зафіксував і передав на землю дані про споруди на поверхні червоної планети в області Кідонії. Ця сенсація була офіційно підтверджена лише у листопаді 1994 р. Тоді Національне управління з аеронавтики та вивчення космічного простору США заявило: “Сфінкс і піраміди на Марсі існують”. У Кідонії було помічено 25 пірамід, з них 5 великих, 20 малих. Сторони основи великих пірамід Марса досягають 1,5 км при висоті в 1 км. Малі піраміди в декілька разів більші великих пірамід Гіз, а весь комплекс розташований на площі 25 км.

Луна задає науковцям не менше загадок, ніж Марс. Фотографії, зроблені американською станцією “Луна-Орбіта-2” у 1966 р. з висоти 48 км, зафіксували у районі Моря Дощів 8 об’єктів правильної пірамідної чи конічної форми. Досліджуючи фото цих пірамід, інженер А.Абрамов виявив, що план розміщення місячних об’єктів 4, 5 і 6 схожий на план розміщення пірамід Хеопса, Хефрена і Мікерина у Гізі. Центри цих вістрів є дзеркальним відображенням вершин трьох єгипетських пірамід.

ЕКОЛОГІЧНА ПІРАМІДА

Піраміда в літературі Брюсов В.Я.

Піраміда в інших галузях На ланах медицині- Знаменита Піраміда Ю-Шеньсе Людська піраміда - так виглядає піраміда суспільства

Підручники XIXст. Тілесний кут, який перерізаний площиною

Основні поняття Піраміда – многогранник, який складається з плоского многокутника – основи піраміди, точки, яка не лежить у площині основи, - вершини піраміди, і всіх відрізків, що сполучають вершину піраміди з точками основи. Відрізки, що сполучають вершину піраміди з вершинами основи, називаються бічними ребрами. Поверхня піраміди складається з основи і бічних граней. Кожна бічна грань – трикутник. Висотою піраміди називається перпендикуляр, опущений з вершини піраміди на площину основи. А В С D O P PABCD – піраміда PA, PB, PC, PD – бічні ребра ABCD – основа піраміди PAD, PAB, PBC, PCD – бічні грані PO – висота

Піраміда Довільна Правильна Зрізана

Піраміда називається правильною, якщо її основою є правильний многокутник, а основа висоти збігається з центром цього многокутника. Площа бічної поверхні правильної піраміди

Площина, яка паралельна основі піраміди й перетинає її, відтинає подібну піраміду

Піраміди в геометрії Правильні многогранники. Переріз пірамід. Тетраедр – трикутна піраміда, всі ребра якої рівні. У правильного тетраедра грані – правильні трикутники. У кожній вершині сходяться по три ребра. Переріз грані площиною є пряма. Для побудови перерізу досить мати в кожній грані дві точки контуру перерізу. Октаедр – це многогранник, який складається з двох пірамід з однією основою. У октаедра грані – правильні трикутники. У кожній вершині сходяться по чотири ребра.

Основні формули стосовно піраміди Назва формули Формула Позначення Площа повної поверхні Sп = S+Sб S – площа основи; Sб – площа бічної поверхні Площа бічної поверхні Sб = Ѕ·P·l Sб = S/ cos α Р – периметр основи; l – апофема; α – двогранний кут при основі Об’єм довільної зрізаної піраміди V = ⅓·H·(S1+S2+√S1·S2) S1,S2 – площі основ; Об’єм правильної зрізаної піраміди P1, P2 – периметри основ Об’єм піраміди V = ⅓·S·H

Серед наведених нижче тверджень укажіть правильні: існує піраміда, яка має 125 ребер; існує піраміда, яка має 125 граней; піраміда може мати два бічні ребра перпендикулярні до основи; сума всіх плоских кутів n-кутної піраміди дорівнює 360°(n-1); якщо одна з бічних граней піраміди перпендикулярна до основи,то висота піраміди збігається з висотою однієї грані.

Твій настрій після уроку:

Д/З: допоможіть цареві: Пише цар і не вгаває: “ Чарівну я шапку маю. Що туди не покладеш - Втроє більш назад візьмеш. Шапка ця чотирикутна, А боки її – трикутні. 30 сантиметрів має Висоту, і не спадає. Ще додам (може, й не в лад): Є основою квадрат, Сторона (лічи вже ти) – Половина висоти. А який об'єм займає Я бажання знати маю. Шапку цю носив мій дід, Тож обчисліть все як слід.” Треба зробити рисунок та, використовуючи формули ,знайти об'єм шапки(піраміди)