Презентація "Теорема Піфагора"
Про матеріал
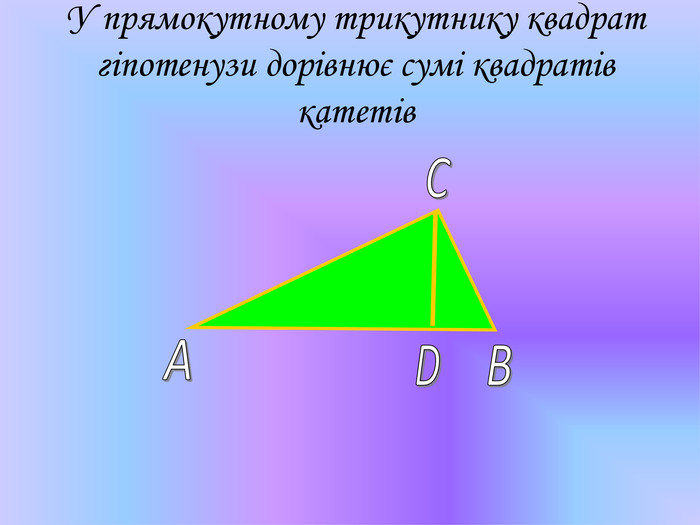
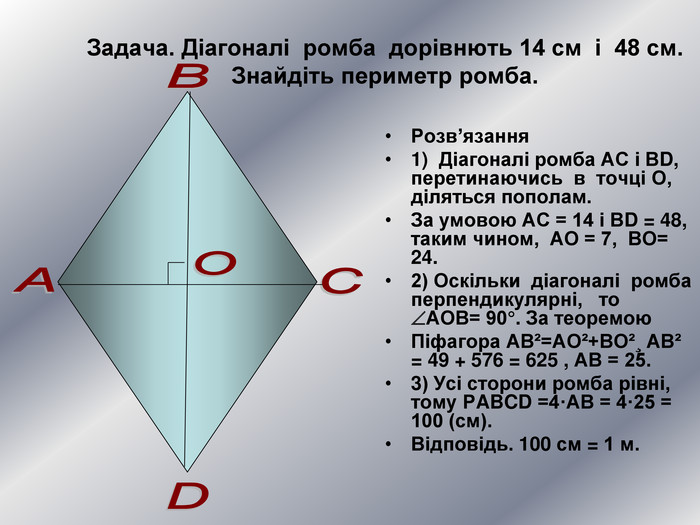
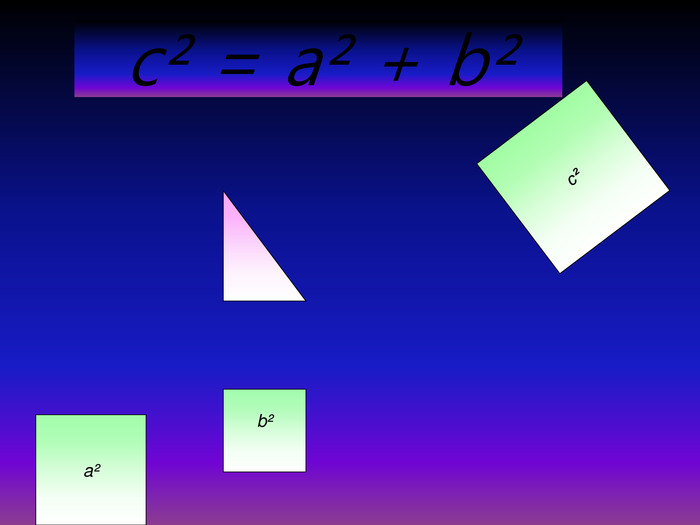
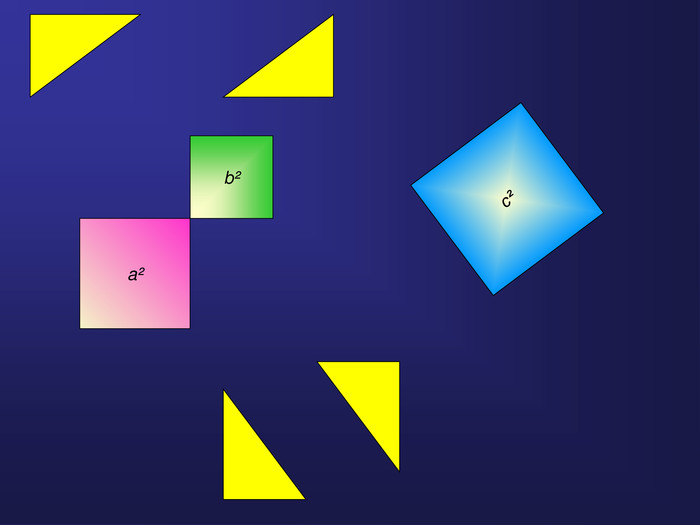
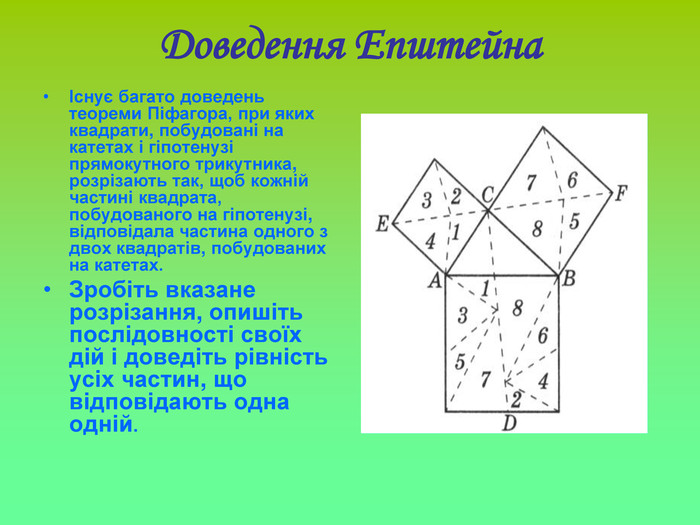
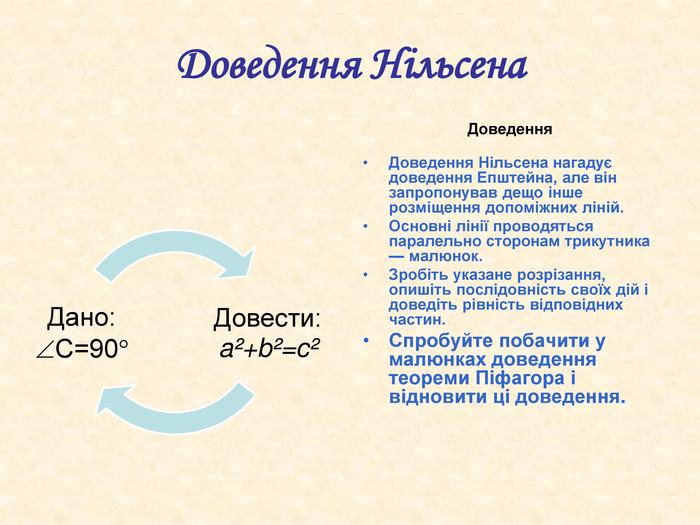
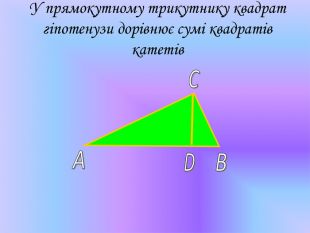
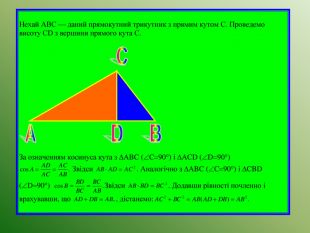
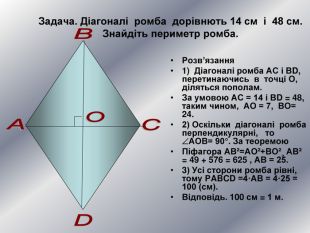
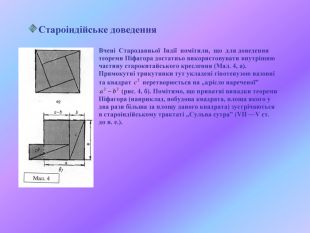
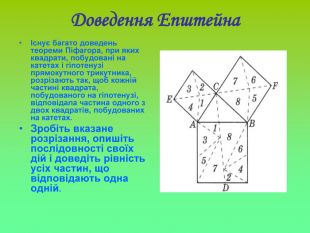
У презентації "Теорема Піфагора" розглянуто різні способи доведення теореми Піфагора. Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку