Урок геометрії у 8 класі "Паралелограм. Ознаки паралелограма"

УРОК № 1

Тема уроку: Паралелограм

 

Мета уроку:

Навчальна:

• дати означення паралелограма;
• познайо­мити учнів з ознаками паралелограма.

Розвиваюча:

• визначати паралелограми на рисунку серед інших фігур;
• формувати первинні вміння застосовувати ознаки під час розв'язування задач.

Пізнавальна:

• за рисунком та символічним позначенням паралелограма називати його кути та сторони, протилежні та сусідні;
• розпізнавати використання тієї чи іншої ознаки в задачі.

Виховна:

• виховувати інтерес до математики, акуратність при побудові малюнків;
• виховувати уміння сконцентруватися, слухати інших, співпереживати, формувати сприятливий моральний клімат.

 

Цілі уроку:

Учні повинні знати:

• означення паралелограма;
• елементи паралелограма;
• ознаки паралелограма.

Учні повинні вміти:

• виконувати зображення паралелограма;
• розпізнавати та називати елементи паралелограма;
• визначати паралелограми на рисунку серед інших фігур;
• використовувати ознаки паралелограма для доведення;
• знаходити помилки на готових малюнках.

 

Тип уроку: засвоєння нових знань.

 

Обладнання: набір демонстраційного креслярського при­ладдя; слайди до уроку ; мультимедійний пристрій ;  індивідуальні картки.

 

Методи, прийоми, форми роботи:  слово вчителя, математичний диктант, рефлексія, інтерактивні вправи: «Пригадай – чому!»,«Знайди помилку», робота в групах - «Ознаки паралелограма», вправа «Дослідження-аналіз».

 

Хід уроку

І. Організаційний момент

Забезпечення емоційної готовності до уроку

Невідомо, хто, коли, але хтось сказав слова, які передаються нам і які ми передаємо вам - нашим нащадкам: «Намагайтеся кожного дня для кожної справи знайти якийсь позитивний початок, оскільки від того настрою,з яким ви вступаєте в новий день, або в якусь справу залежать ваші успіхи, а можливо, і невдачі». Я бажаю вам розпочати урок з гарним настроєм і отримати від нього задоволення і гарні результати.

 

ІІ. Перевірка домашнього завдання

 

1. Математичний диктант

Методична ремарка

Вчитель усно диктує завдання, а потім результат написання диктанту перевіряється за допомогою слайду 1.

 

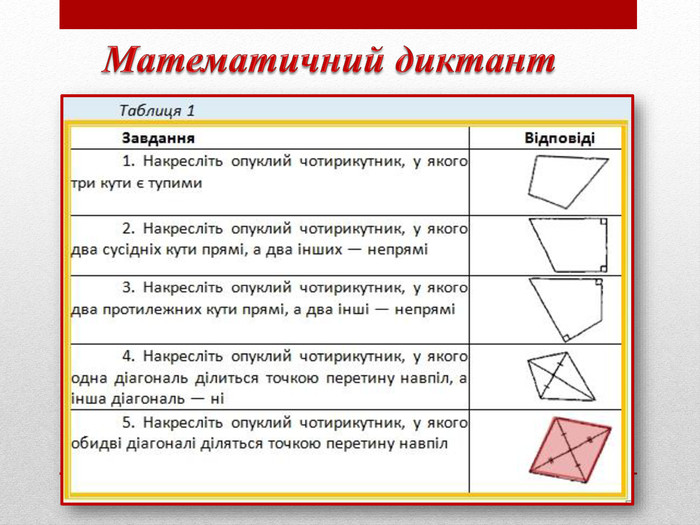
Слайд  1

Завдання	Відповіді
1. Накресліть опуклий чотирикутник, у якого три кути є тупими
2. Накресліть опуклий чотирикутник, у якого два сусідніх кути прямі, а два інших — непрямі
3. Накресліть опуклий чотирикутник, у якого два протилежних кути прямі, а два інші — непрямі
4. Накресліть опуклий чотирикутник, у якого одна діагональ ділиться точ­кою перетину навпіл, а інша діаго­наль — ні
5. Накресліть опуклий чотирикутник, у якого обидві діагоналі діляться точ­кою перетину навпіл

Методична ремарка

Після диктанту вчитель пропонує учням зробити самоперевірку диктанту, відповідає на питання, що виникли під час перевірки.

 

ІІІ. Формулювання мети і задач уроку. Мотивація навчальної діяльності.

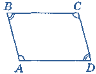
1. Слово вчителя.Діти, подивіться на ці п’ять чотирикутників. Серед них є незвичайний, особливий чотирикутник. Гармонійний – у багатьох відношеннях! Над його побудовою, його ознаками ми і будемо сьогодні працювати! Який саме? Дізнаємось … незабаром!

 

IV. Актуалізація опорних знань учнів.

 

1. Вправа «Пригадай – чому!»(Учням пропонується три рисунка, по яких потрібно за вказівкою вчителя виконати завдання)

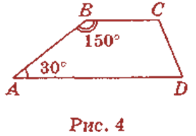
1.               Вкажіть пари внутрішніх різносторонніх кутів і пари внутрішніх односторонніх кутів на рис. 3. Чи є прямі с і d паралельними, якщо:

a) 1=4;       б) 1 = 60°, 3 = 120°?

 

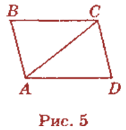
2.               На рис. 4 A = 30°, В = 150°. Доведіть, що BC || AD.

 

3.               AC — діагональ чотирикутника ABCD (рис. 5). Доведіть, що BC || AD і AB || CD, якщо ∆ABC = ∆CDA.

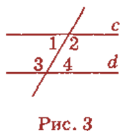
  Рисунки – на дошці

 

V. Вивчення нового матеріалу

 

1.Пояснення вчитель здійснює за допомогою проектної таблиці на слайді.

 

Слайд  2

	Означення паралелограма
		Паралелограм — це чотирикутник, у якого протилежні сторони паралельні (тобто ле­жать на паралельних прямих)
	Ознаки паралелограма
1.		Якщо діагоналі чотирикутника перетина­ються та діляться точкою перетину навпіл, то цей чотирикутник — паралелограм
2.		Якщо в чотирикутнику дві протилежні сто­рони рівні і паралельні, то цей чотирикут­ник — паралелограм
3.		Якщо в чотирикутнику протилежні сторо­ни попарно рівні, то цей чотирикутник — паралелограм
4.		Якщо в чотирикутнику протилежні кути попарно рівні, то цей чотирикутник — па­ралелограм

 

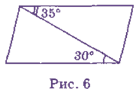
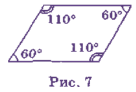
2. Вправа «Знайди помилку»( із одним безпомилковим завданням!)

Які помилки допущені в зображенні паралелограмів на рис. 6 і 7?

  Рисунки – на дошці

 

3. Робота в групах - «Ознаки паралелограма»

Учитель об'єднує учнів у чотири групи таким чином, щоб у кож­ній з них були учні з різним рівнем підготовки. Кожній групі в якості задачі на доведення пропонується довести одну з ознак паралело­грама, наведених у таблиці. Якщо необхідно, вчитель надає групам допомогу. Група, яка закінчує першою має змогу представити своє доведення класу. Інші здають свої  проекти вчителю на перевірку. Учитель підкреслює, що ці твердження є ознаками паралелограма й часто застосову­ються при розв'язуванні задач.

 

Орієнтовне доведення ознак

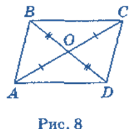
Задача 1 (ознака 1). Якщо діагоналі чотирикутника перетина­ються і точкою перетину діляться навпіл, то цей чотирикутник — паралелограм.

Доведення

Нехай ABCD— даний чотирикутник, діагоналі якого перетинають­ся в точці О (рис. 8). У трикутниках ВОС і DOA: BO = DO, OC = OA — за умовою; BOC= DOA як вертикальні. Отже, ∆ВОС = ∆DOAза двома сторонами і кутом між ними. Звідси BCO = DAO, при­чому ці кути є внутрішніми різносторонніми при прямих ВС і AD і січній АС. Отже, ВС || AD. Аналогічно доводимо рівність трикут­ників BOA і DOC і паралельність прямих АВ і CD. Оскільки проти­лежні сторони чотирикутника паралельні, то цей чотирикутник — паралелограм за означенням, що й треба було довести.

 

Задача 2 (ознака 2). Якщо в чотирикутнику дві протилежні сто­рони рівні і паралельні, то цей чотирикутник — паралелограм.

Доведення

Нехай у чотирикутнику ABCD(рис. 9) АВ || CD, АВ = CD. У дано­му чотирикутнику проведемо діагональ АС. Оскільки АВ || CD, а АС — січна, то ВАС = DCA як внутрішні різносторонні при паралельних прямих і січній. АС — спільна сторона трикутників ВАС і DCA, AB = CDза умовою. Отже, ∆BAC =∆DCAза двома сторонами і ку­том між ними. Звідси ВСА = DAC. Оскільки ці кути внутрішні різносторонні при прямих ВС і AD і січній АС, то BC || AD. Отже, AB || CD, ВС || AD. Таким чином, у чотирикутнику ABCDпротилежні сторони паралельні, отже, він паралелограм за означенням, що й треба було довести.

  

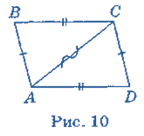
Задача 3 (ознака 3). Якщо в чотирикутнику протилежні сторони попарно рівні, то цей чотирикутник — паралелограм.

Доведення

Нехай у чотирикутнику ABCD(рис. 10) АВ = CD, ВС = AD. У да­ному чотирикутнику проведемо діагональ АС. У трикутниках ABCі CDA: AB = CD, BC = AD— за умовою, АС — спільна сторона. Отже, ∆ABC = ∆CDA за трьома сторонами. Звідси BAC = DCA, BCA = DAC як відповідні кути рівних трикутників. Оскільки кути ВАС і DCA — внутрішні різносторонні при прямих АВ і CD і січній АС, а кути ВСА і DAC — внутрішні різносторонні при пря­мих ВС і AD і січній АС, то відповідно АВ || CD, BC || AD. Отже, чотирикутник ABCD— паралелограм за означенням, що й треба було довести.

 

Задача 4 (ознака 4). Якщо в чотирикутника протилежні кути попарно рівні, то цей чотирикутник — паралелограм.

Доведення

Як уже було доведено, сума кутів будь-якого чотирикутника дорівнює 360°. Нехай у чотирикутнику ABCD (рис. 11) A = C, B = D. Оскільки A + B + C + D= 360°, то 2(A + B) = 360°. Звідси A + B = 180°. Оскільки кути А і В — внутрішні односто­ронні при прямих ВС і AD і січній АВ, то ВС || AD за ознакою па­ралельності прямих. Аналогічно A + D = 180°, отже, AB || CD. Отже, чотирикутник ABCD — паралелограм за означенням, що й треба було довести.

  

VI. Фізкультхвилинка.

І направо, і наліво,

Щоб нічого не боліло.

Один і два, три і чотири —

Набираємося сили.

Нахилились, повернулись,

До товариша всміхнулись.

 

VIІ. Первинне закріплення нових знань учнів

 

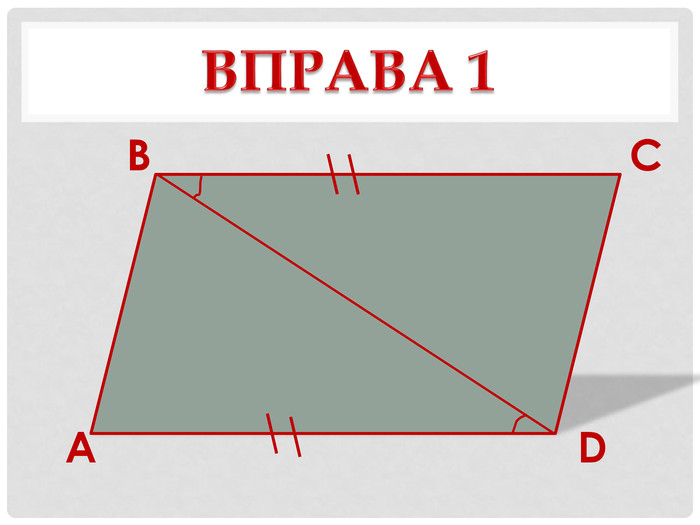
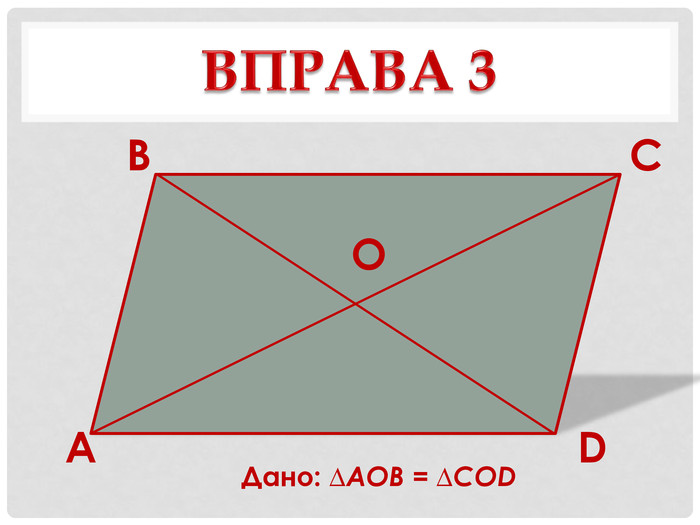
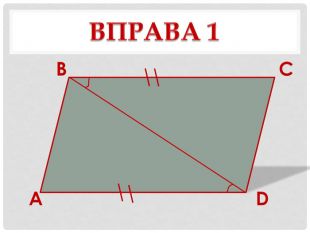
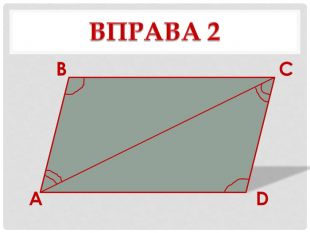
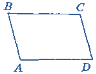
1. Вправа «Дослідження-аналіз» - виконання усних вправ за готовими рисунками – на слайдах презентації. (учням потрібно довести для кожного з випадків, зображених на чотирьох слайдах,  що чотирикутник ABCD— паралелограм).

Слайд  1       Слайд  2

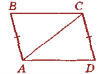
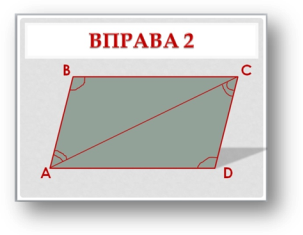
аа)		б б)
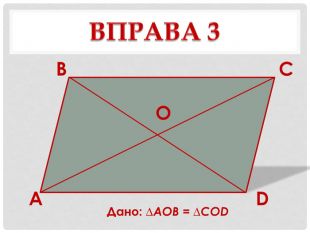
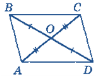
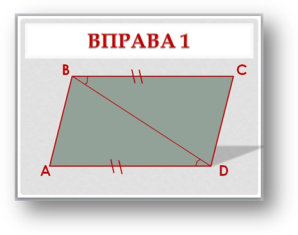
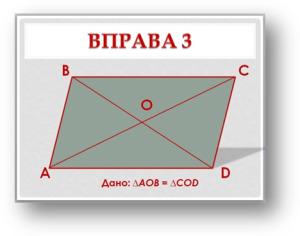
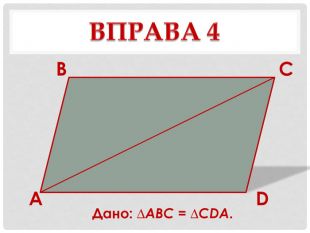
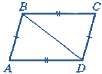
в) Дано: ∆АОВ = ∆COD.		г) Дано: ∆АВС = ∆CDA.

 

Слайд  3       Слайд  4

 

2. Робота в зошитах(колективно під керівництвом учи­теля)

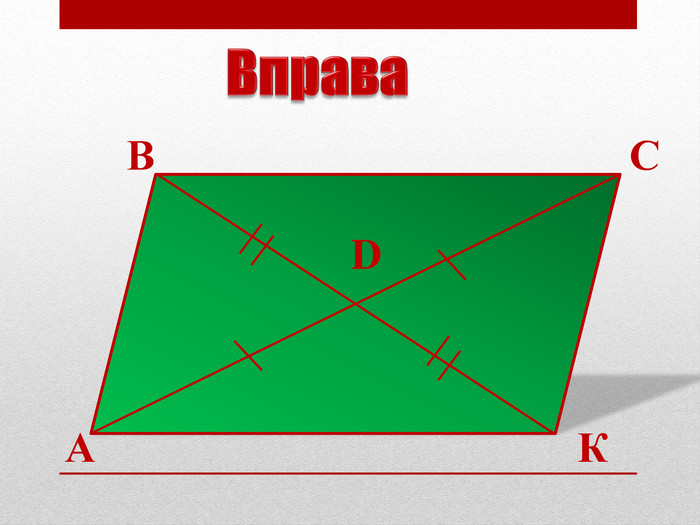
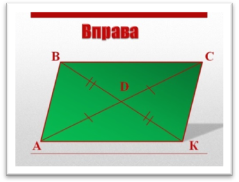Задача. У трикутнику ABC (рис. 13) на продовженні медіани BD відкладено відрізок DK, рівний BD. Доведіть, що АВСК — парале­лограм.

Доведення

Оскільки BD — медіана трикутника ABC, отже, AD = DC. BD = DK за умовою, таким чином, у чотирикутнику АВСК діагоналі ді­ляться точкою перетину навпіл. Отже, АВСК — паралелограм за ознакою, що й треба було до­вести.

 

Слайд  5

 

 

 

 

VIІI.Підбиття підсумків уроку

 

1. Бесіда.

•                   З якою фігурою познайомилися? Так, яка ж вона була серед п’яти на початку уроку?
•                   А чому ж він такий майже досконалий? Що ж в ньому такого цікавого?
•                   Щоб чотирикутник був паралелограмом, які повинні справджуватися умови?

 

2. Рефлексія.

- Сьогодні на уроці я дізнався…..

- Мені сподобалося…

- Я запам’ятаю…

 

ІХ. Домашнє завдання

1. Вивчити означення та ознаки паралелограма.
2. Розв’язати задачі:

 

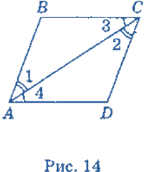1. Дано:  1 = 2; 3 = 4  (рис. 14). Довести: ABCD— паралелограм.

  

 

 

 

 

 

 

 

 

2. Побудуйте паралелограм за двома сторонами 5 см і 7 см та кутом 55°. (Вка­зівка: під час побудови використовуйте ознаку паралелограма).