Презентація " Теорема Піфагора"
Про матеріал
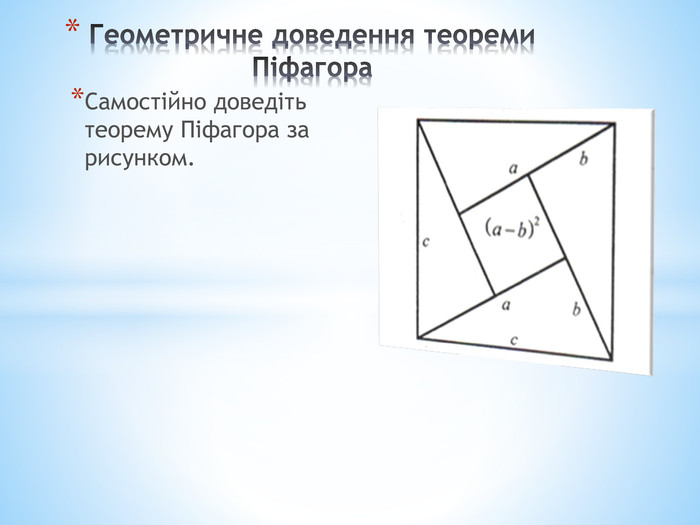
Презентація для учнів 8 класу при вивченні теореми Піфагора. Презентація містить біографічні дані про Піфагора, деякі способи доведення теореми, типи розв'язування задач на застосування теореми Піфагора, обернену теорему та спосіб побудови прямого кута на поверхні землі. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку