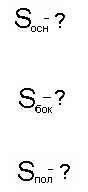Узагальнюючий урок по темі "Призма"

 

Узагальнюючий урок по темі «Призма »

 

Мета: систематизувати знання учнів по темі «Призма». Закріпити вміння правильно формулювати властивості й визначення фігур. Розширити знання учнів по темі. Формувати дружні, товариські відносини вміння працювати в групах.

Обладнання: моделі геометричних фігур, мультимедійний проектор, екран.

 

Хід уроку

1. Організаційний момент.

Вітання вчителя.

Вчитель

Сьогодні урок геометрії по темі «ПРИЗМА» проведемо у вигляді ВІДКРИТОГО ЗАСІДАННЯ АМАТОРІВ БАГАТОГРАННИКІВ. Розглянемо основні види призм: трикутну, чотирикутну, шестикутну. Ви маєте показати свої знання по темі «Багатогранник. Призма», розширити свої знання, побудувати моделі багатогранників.

У засіданні клубу беруть участь три групи.

Давайте визначимо,

Правила засідання: (на дошці записані)

1. На засідання виноситься чотири питання

1. подання фігур
2. тестування
3. перерізу...перерізу
4. розгорнення

2. На кожному етапі передбачаються питання, завдання з варіантами відповідей або із планом розв'язання.

3. Відповіді оцінюються й заносяться в оцінний аркуш.

4. На дошці фіксуються відповіді команд.

2.  Засвоєння знань

1 етап «Подання»

РОЗГЛЯНЕМО ПЕРШЕ ПИТАННЯ ЗАСІДАННЯ

(робота з визначеннями , поняттями)

Вчитель

ЗАВДАННЯ 1. Потрібно прославити фігуру своєї команди.

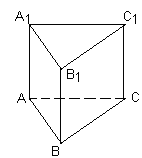
1 ГРУПА – ПРЕДСТАВЛЯЄ ТРИКУТНУ ПРИЗМУ

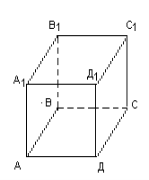
2 ГРУПА – ЧОТИРИКУТНУ ПРИЗМУ

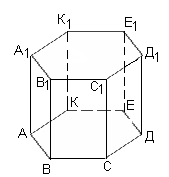
3 ГРУПА – ШЕСТИКУТНУ ПРИЗМУ

На картках написані питання, а на окремих листочках відповіді.

Знайти для кожного питання відповідь.

Учні працюють у групах

	Питання	Відповіді
Трикутна ПРИЗМА
1	Що таке трикутна призма?	Багатогранник складений із двох рівних трикутників, які розташовані у двох паралельних площинах і трьох паралелограмів називається …...
2	Як взаємно розташовані бічні ребра призми?	Бічні ребра призми рівні й паралельні
3	Що можна сказати про основи призми, бічних гранях?	Основи призми є рівні трикутники, бічні грані – це паралелограми, якщо призма пряма то грані – прямокутники
4	Визначити елементи трикутної призми.	Ребер – 9, вершин – 6, граней – 5
5	Скільки діагоналей у трикутної призми?	Призма не має діагоналей
Чотирикутна ПРИЗМА
1	Що таке чотирикутна призма?	Багатогранник складений із двох рівних чотирикутників, які розташовані у двох паралельних площинах і чотирьох паралелограмів називається …...
2	Визначити елементи чотирикутної призми.	Ребер – 12, вершин – 8, граней – 6
3	Чим є бічні грані призми, підстави чотирикутної призми?	Підстави призми є рівні чотирикутники, бічні грані – це паралелограми, якщо призма пряма то грані – прямокутники
4	Чи є паралелепіпед призмою?	Паралелепіпед - це призма, у підставі якої лежить  паралелограм.
5	Скільки діагоналей у чотирикутної  призми?	В... …призмі можна провести  чотири діагоналі.
Шестикутна ПРИЗМА
1	Що  таке шестикутна призма?	Багатогранник складений із двох рівних шестикутників, які розташовані у двох паралельних площинах і шести паралелограмів називається …...
2	Визначити елементи шестикутної призми.	Ребер – 18, вершин – 12, граней – 8.
3	Чим є основи  й бічні грані шестикутної призми ?	Основи призми є рівні шестикутники, бічні грані – це паралелограми, якщо призма пряма те грані – прямокутники
4	Скільки діагоналей у шестикутної призми?	В... …. призмі можна провести   12  діагоналей.
5	Коли призма називається прямій?	Якщо бічні ребра призми перпендикулярні  до основ  то призма називається…...

 

Вчитель

А ТЕПЕР ПЕРЕВІРЯЄМО ВАШІ ВІДПОВІДІ. ЧИ БУЛИ ПОМИЛКИ? КОМАНДИ ОДЕРЖУЮТЬ (оцінки)

(відповіді на кожне питання демонструються на слайдах)

 

Вчитель

УВАЖНІ БУЛИ?

Ще вчений Эйлер - геній 18 століття вивів залежність між гранями, вершинами, ребрами для призм. Ця  залежність увійшла в історію математики як ТЕОРЕМА Эйлера. Зрозуміло, що залежно від того яку основу буде мати призма, буде змінюватися кількість  її граней , ребер.  У таблиці допущені помилки. ЗНАЙДІТЬ ЇХ, ХТО ШВИДШЕ ТОЙ ОДЕРЖУЄ ДОДАТКОВИЙ БАЛ. ( матеріал на слайді)

Теорема Эйлера

Г + В = Р + 2

 

	Г(грані)	В(вершини)	Р(ребра)
	3/5	6	9
	6	4/8	12
	8	12	6/18

 

 

 

 

Вчитель

ПЕРШИЙ ЕТАП НАШОГО ЗАСІДАННЯ МИ РОЗГЛЯНУЛИ, ПЕРЕХОДИМО ДО ДРУГОГО ПИТАННЯ.

 

2 етап «Аматори тестів»

Вчитель

ЗАВДАННЯ 2: вибрати правильні відповіді, з отриманих букв скласти 3 слова, по яких ви довідаєтеся яких принципів потрібно дотримуватися в житті.

1 ГРУПА працює по темі «Чотирикутна призма»

2 ГРУПА працює по темі «Шестикутна призма»

3 ГРУПА працює по темі «Трикутна призма»

 

	Питання	Відповіді (РОЗУМІТИ,ПРИЙМАТИ, ДОПОМАГАТИ)
Трикутна ПРИЗМА
1	Багатокутники з яких складені багатогранники - це ...	К) ребра;  Р) грані;  В) вершини;  Г) висоти.
2	Перпендикуляр, проведений з якої-небудь крапки однієї основи до площини іншої основи називається...	О) висота;  Р) пряма;  В) грань;  Г) вершина.
3	У трикутній призмі можна провести діагональ.	К) так;  З) ні.
4	У основі трикутної призми може лежати рівнобедрений трикутник	У) так;  Л) ні.
5	У правильній трикутній призмі в основі лежить	С) рівнобедрений трикутник; М) рівносторонній трикутник; В) прямокутний трикутник.
6	Трикутна призма має ....ребер	Г) 6;  Р) 5;  І) 9.
7	Бічні грані прямої трикутної призми…	О) квадрати;  Т) прямокутники; В) трикутники.
8	Якщо в основі прямої призми лежить правильний багатокутник то призма називається…	Ю) трикутна;  Б) пряма; В)похила;   И) правильна.
Чотирикутна ПРИЗМА
1	Багатогранник, що розташований по один бік від площини кожної його грані називається…	П) опуклим;  Б) не опуклим.
2	У основі чотирикутної призми  може лежати ромб.	Р) так;  Б)ні.
3	Скільки вершин має куб?	А) 4;  И) 8;  О) 6;  Ы) 12.
4	Правильна чотирикутна призма – у основі лежить	Р) ромб;  Й) квадрат;  В) прямокутник.
5	Прямокутний паралелепіпед – це призма	М) так;  А)ні.
6	Бічні грані прямої чотирикутної призми…	О) квадрати;  А) прямокутники; В) трикутники.
7	Якщо бічні ребра призми перпендикулярні до основ то призма…	Г) правильна;  Т)пряма;  В) похила.
8	Якщо в основі прямої призми лежить правильний багатокутник то призма називається…	А) трикутна;  Д) пряма; В)похила;   И) правильна.
Шестикутна  ПРИЗМА
1	Грані – це багатокутники, з яких складений багатогранник	Д) так;   Б)ні.
2	Шестикутна  призма  має ....ребер	Ю) 6;  А) 5;  Г) 9;  О) 18.
3	Бічні грані прямої шестикутної призми…	К) квадрати;  П) прямокутники; В) трикутники.
4	Правильна шестикутна  призма – у підставі лежить	А) ромб;  Р) квадрат;  Ю) прямокутник; О) правильний шестикутник.
5	У шестикутній  призмі можна провести діагональ.	М) так;  Б) ні.
6	Якщо бічні ребра призми перпендикулярні до основи то призма...	К) правильна;  О)пряма;  В) похила.
7	Якщо в основі прямої призми лежить правильний багатокутник то призма називається…	Р) шестикутна;  Б) пряма; В)похила;  ГА) правильна.
8	Куб – це шестикутна призма	Ю) так;  ТИ) ні.

(на слайді по черзі з'являються слова: РОЗУМІТИ, ПРИЙМАТИ, ДОПОМАГАТИ)

Вчитель

Молодці! Команди впоралися із завданнями. Ви довідалися, яких принципів потрібно дотримуватися в житті. Я вам бажаю успіхів, нехай ці слова йдуть і з вами по життю. (Кожна команди одержують оцінки)

 

 

Вчитель -завдання на увагу.

УВАГА! «Чарівний слайд» Що зашифровано?

(Призма, у підставі правильний багатокутник, можна провести діагоналі, діагональні перетини -прямокутники, має 6 граней, 12 ребер -рівні, 8 вершин) - КУБ

 

МИ РОЗГЛЯНУЛИ ДРУГИЙ ЕТАП НАШОГО ЗАСІДАННІ. ПЕРЕХОДИМО ДО ТРЕТЬОГО ПИТАННЯ.

 

3 етап «Перерізу...перерізу»

Вчитель

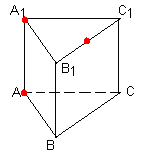
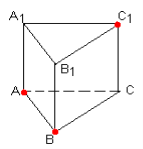
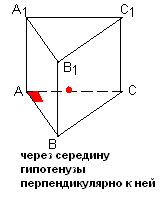
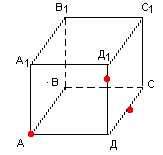
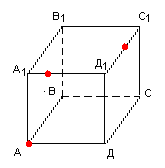
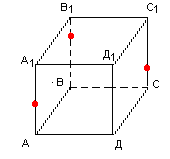
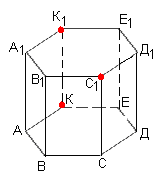
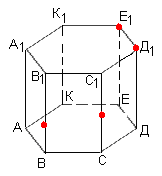
ЗАВДАННЯ 3: ПОБУДУВАТИ ПЕРЕРІЗ, ЩО ПРОХОДИТЬ ЧЕРЕЗ ДАНІ ТОЧКИ Й ВИЗНАЧИТИ ЯКИЙ БАГАТОКУТНИК ВИЙШОВ ПРИ ПОБУДОВІ.

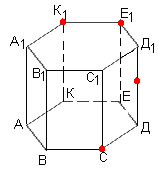
1 ГРУПА працює по темі «Шестикутна призма»

2 ГРУПА працює по темі «Трикутна призма»

3 ГРУПА працює по темі «Чотирикутна  призма»

Завдання підібрані за принципом «від простого до складного»

 

	«3»	«4»	«5»
Трикутна   призма
Чотирикутна   призма
Шестикутна призма

 

На дошці фіксують готові відповіді. Отримані бали заносять в оцінні аркуші

Вчитель

МИ РОЗГЛЯНУЛИ ТРЕТЄ ПИТАННЯ ЗАСІДАННЯ

ФІЗКУЛЬТХВИЛИНКА

Завдання: На слайдах з’являються формули знаходження площі основних багатокутників, якщо діти згодні - то ПІДНІМАЮТЬ РУКИ, якщо ні – качають головою.

(площа трикутника, площа ромба, площа трапеції, площа  квадрата, площа паралелограма)

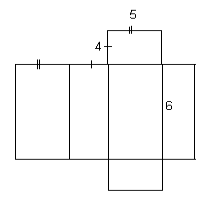
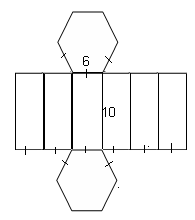
4 етап «Розгорнення»

Вчитель

Засідання клубу триває й ОСТАННЄ ПИТАННЯ ЗАСІДАННЯ – «Розгорнення». Всі багатогранники розташовані на ваших столах, всі будови які зараз нас оточують, будувалися за принципом склеїти, побудувати.

Важливу роль займає розгорнення. Вона дає відповідь на питання:

З ЯКИХ БАГАТОКУТНИКІВ СКЛАДАЄТЬСЯ ПРИЗМА.

 

ЗАВДАННЯ 4.

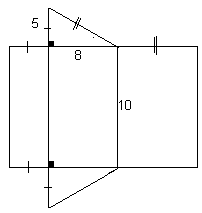
За даними розгорненнями

1. Зробити креслення багатогранника
2. Зробити модель багатогранника
3. Знайти повну поверхню призми

РОЗГОРНЕННЯ	КРЕСЛЕННЯ	ПОВНА ПОВЕРХНЯ

 

Вчитель

Ми розглянули останнє питання засідання клубу аматорів багатогранників. Команди одержують оцінки. Хто не впорався із завданням, продовжимо роботу на наступному уроці.

Вчитель

4. Підсумок уроку (на слайді)

Вчений П.Л. Чебишев казав: «Зближення теорії із практикою дає самі доброчинні результати» –   у чому ми з вами сьогодні переконалися.

 

УЧАСНИКИ КОМАНД ОДЕРЖУЮТЬ - ОЦІНКИ,

(команди виявили себе як  сильні, енергійні особистості, вміють аналізувати, робити висновки, проявили працьовитість, наполегливість, ретельність

Вчитель

5. Домашнє завдання ( на слайді)

 

 

 РОЗГЛЯНЕМО ДОМАШНЄ ЗАВДАННЯ.

 Лабораторно-практична робота

 

1. Побудувати багатогранник
2. Виконати переріз
3. Знайти площу перерізу
4. Знайти повну поверхню призми
5. Накреслити розгорнення
6. Виконати модель призми

 

На цьому я хочу засідання клубу завершити.

Спасибі всім. До нових зустрічей!