Підготовка до ЗНО                                                                                                           8 – 12 клас

 

НА ДОПОМОГУ ВЧИТЕЛЮ

 

 

ГОТУЄМОСЯ ДО ЗОВНИШНЬОГО НЕЗАЛЕЖНОГО ОЦІНЮВАННЯ.

ПЛАНІМЕТРІЯ.

 

 

«СИСТЕМА ВПРАВ  З ТЕМИ «ПЯМОКУТНИЙ ТРИКУТНИК» ДЛЯ

СИСТЕМАТИЗАЦІЇ І УЗАГАЛЬНЕННЯ ЗНАНЬ І ВМІНЬ УЧНІВ З

ГЕОМЕТРІЇ» 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема "Трикутники"- одна з найважливіших тем у геометрії. Від глибокого її вивчення залежать подальші успіхи в геометрії. Проблема вивчення основних «китів» шкільного курсу геометрії  7 – 9 класів дуже гостро встає у старшій школі, колі усі завдання стереометрії опираються на знання планіметрії , у тому числі на знання прямокутного трикутника. Часу на повторення  не має, а шкільний підручник з геометрії виявляється поганим помічником.

Система вправ,  яка підібрана мною,  дозволяє повторити усі формули прямокутного трикутника.

В добірку завдань вийшли завдання ЗНО починаючи з 2008 року. 

 

 

СИСТЕМА ВПРАВ З ТЕМИ «ПРЯМОКУТНИЙ ТРИКУТНИК»  

1. Завдання з вибором однієї правильної відповіді

1.        Знайдіть гіпотенузу прямокутного трикутника з катетами 12 см і 5 см.

А) 49 см            Б) 7 см               В)  119 см        Г) 169 см           Д) 13 см

                                         

2.        Доберіть таке закінчення речення, щоб утворилося правильне твердження:

«Сума квадратів катетів прямокутного трикутника дорівнює …»

А) гіпотенузі              Б) квадрату            В) квадрату             Г) добутку             Д) подвійному

                                               суми катетів            гіпотенузи                 катетів               добутку катетів

                                         

3.        Знайдіть невідомий катет  прямокутного трикутника, у якого гіпотенуза дорівнює 26 см, а один з катетів 10 см

А) 576 см          Б) 24 см             В) 12 см            Г) 16см              Д)  776 см

                                         

4.        Знайдіть косинус меншого кута прямокутного трикутника, гіпотенуза і більший катет якого дорівнюють відповідно 10 см і 8 см.

3                                                           4            ^{5              5              3}

А)                      Б)                      В)                      Г)                      Д) 

        5                                       5                                         3                                        4                                         4

                                         

5.        Знайдіть синус більшого кута прямокутного трикутника, катети якого дорівнюють 9 см і 12 см.

А) 3                    Б) ⁴                    В) ⁵                   Г) ⁵                    Д) ³

        5                                       5                                         3                                        4                                         4

                                         

6.        Знайдіть тангенс більшого кута прямокутного трикутника, гіпотенуза і менший катет якого дорівнюють відповідно 20 см і 12 см.

        4                                       4                                         ^{5                                        5                                         3}

А)                      Б)                      В)                      Г)                      Д) 

3                                                           5            3              4              4

                                         

7.        У прямокутному трикутнику катет дорівнює 10 2 см, протилежний кут дорівнює 45⁰. Знайдіть довжину відрізка, який  з’єднує   середини катетів трикутника.

А) 20 см            Б) 5 см               В) 5 2 см           Г) 10 2 см         Д) 10 см

                                         

8.        В прямокутному трикутнику градусна міра одного з кутів 25⁰. Знайдіть градусну міру другого гострого кута трикутника.

А) 20⁰                           Б) 55⁰                           В) 65⁰                           Г) 75⁰                           Д) 45⁰

                                         

9.        Знайдіть площу прямокутного трикутника з катетами 8 см і 15 см.

А) 60 см²                  Б) 120 см²          В) 11,5 см²        Г) 127,5 см²       Д) 68 см²

 

10.   Знайдіть площу прямокутного трикутника з гіпотенузою 17 см і катетом 15 см.

А) 60 см²                  Б) 120 см²          В) 11,5 см²        Г) 127,5 см²       Д) 68 см²

                                         

11.   Площа прямокутного трикутника дорівнює 84 см², а один з катетів 12 см. Знайдіть другий катет трикутника.

А) 7 см              Б) 12 см             В) 14 см             Г)  340 см         Д) 28 см

                                         

12.   Площа прямокутного трикутнику дорівнює 96 см². Один з катетів дорівнює 16 см. Знайдіть гіпотенузу трикутника.

А) 20 см            Б) 10 см             В) 12 см            Г) 16 см             Д)  292 см

                                         

13.   Знайдіть площу прямокутного трикутнику гіпотенуза якого дорівнює 26 см, а висота проведена до неї 10 см. 

А) 72 см²                  Б) 240 см²         В) 260 см²         Г) 120 см²          Д) 130 см²

                                         

14.   Висота прямокутного трикутнику, яка проведена до гіпотенузи поділяє ії на відрізки 6 см і 24 см. Знайдіть площу трикутника.

А) 180 см²    Б) 360 см²   В) 144 см²   Г) 72 см²     Д) визначити неможливо

                                         

15.   Висота прямокутного трикутнику, яка проведена до гіпотенузи поділяє ії на відрізки 6 см і 24 см. Знайдіть більший катет трикутника.

А) визначити Б) 18 см   В) 6 5 см     Г) 12 5 см   Д) 30 см неможливо

                                         

16.   Гіпотенуза трикутника дорівнює 12 см, а один з  кутів 30⁰. Знайдіть менший катет трикутника.

А) 6 см              Б) 12 см             В) 6 3 см           Г) 6 2 см            Д) 12 3 см

                                         

                                         

17.   Гіпотенуза трикутника дорівнює 18 см, а один з  кутів 60⁰. Знайдіть менший катет трикутника.

А) 9 см              Б) 18 см             В) 18 3 см         Г) 9 2 см            Д) 9 3 см

                               

18.   Катет трикутника дорівнює 12 см, а прилеглий кут 60⁰. Знайдіть гіпотенузу трикутника.

А) 12 см            Б) 15 см             В) 24 см             Г) 12 3 см         Д) 24 3 см

                                         

19.   Катет трикутника дорівнює 9 см, а протилежний кут 30⁰. Знайдіть площу трикутника.

А) 81 см²                  Б) 162 см²          В) 40,5 см²         Г) 81 3 см²           Д) 162 3 см²

                                         

20.   Знайдіть площу прямокутного трикутника з гіпотенузою 10 2 см і кутом

45⁰.

А) 10 см²                  Б) 100 см²                В) 50 см²                  Г) 20 см²                   Д) 150 см²

                                         

21.   Знайдіть радіус кола вписаного в прямокутний трикутник з катетами 3 см і 4 см.

А) 6 см              Б) 2 см               В) 3 см              Г) 5 см              Д) 1 см

                                         

22.   Знайдіть радіус кола описаного навколо прямокутного трикутника з катетами 15 см і 8 см.

А) 8,5 см           Б) 17 см             В) 6 см              Г) 11,5 см          Д) 20 см

                                         

23.   Радіус кола описаного навколо прямокутного трикутника дорівнює 13 см, один з катетів дорівнює 24 см. Знайдіть периметр трикутника.

А) 47 см            Б) 74 см             В) 61 см            Г) 50 см             Д) 60 см

                                         

24.   Катети прямокутного трикутника дорівнюють 6 см і 8 см. Знайдіть висоту трикутника, проведену до гіпотенузи. 

А) 4,8 см           Б) 2,4 см            В) 48 см            Г) 24 см             Д) 10 см

                                         

25.   Катет та гіпотенуза прямокутного трикутника відповідно дорівнюють 12 см і 30 см. Знайдіть проекцію цього катета на гіпотенузу.

А)  756 см         Б) 2,5 см            В) 2,4 см           Г) 9,6 см            Д) 4,8 см

                                         

26.   Знайти гіпотенузу прямокутного трикутника, у якого висота, проведена до гіпотенузи, дорівнює 12 см, а проекція одного з катетів на гіпотенузу дорівнює 24 см

А) 24 см            Б) 30 см             В) 36 см            Г) 28 см             Д) 32 см

                                         

                               

27.   Один з катетів трикутника дорівнює 16 см, а гіпотенуза 20 см. Знайти менший з відрізків, на які поділяє гіпотенузу бісектриса прямого кута.

А) 6 см              Б) 5 см               В)  см            Г)  см          Д)  см

28.   Знайти площу прямокутного трикутника, у якого бісектриса прямого кута діліть гіпотенузу на відрізки завдовжки  см і  см.

А) 48 см²                  Б) 96 см²                   В) 72 см²                  Г) 24 см²                    _Д)  

                                         

29.   Знайти тангенс більшого кута прямокутного трикутника, у якого бісектриса прямого кута діліть гіпотенузу на відрізки завдовжки 4 см і 8 см.

А) 2                   Б) 0,5                 В) 1                    Г)  3                  Д)  3

3

                                         

30.   У прямокутному трикутнику один з гострих кутів дорівнює 32⁰. Знайти кут між бісектрисою і висотою трикутника, проведених з вершини прямого кута.

А) 18⁰                           Б) 32⁰                           В) 26⁰                           Г) 13⁰                           Д) 58⁰

                                         

31.   У прямокутному трикутнику один з гострих кутів дорівнює 32⁰. Знайти кут між медіаною і висотою трикутника, проведених з вершини прямого кута.

А) 23⁰                           Б) 26⁰                           В) 32⁰                           Г) 33⁰                           Д) 36⁰

                                         

32. 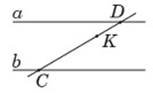  На рисунку зображено паралельні прямі а і b та січну СD. Знайдіть відстань між прямими а і b, якщо СК = 5 см, КD = 2 см, а відстань від точки К до прямої а дорівнює 1 см. 

А) 2,5 см           Б) 3 см               В) 3,5 см           Г) 4 см              Д) 4,5 см

                                         

 

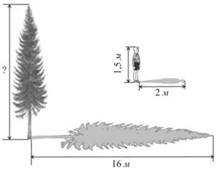
33.   У сонячний день довжина тіні від дерева становіть 16 м. У той же самий час тінь від хлопчика, який має зріст 1,5 м, дорівнює 2 м (див. рисунок). Визначте висоту дерева. 

А) 12 м              Б) 12,5 м            В) 13 м              Г) 14 м              Д) 15,5 м

                                         

34.   У гострокутному трикутнику АВС проведено висоту ВМ. Визначте довжину сторони АВ, якщо ВМ = 12, ∟А = α.

           А)          В) 12 tgα           Г) 12 sinα           Д) ¹²

 

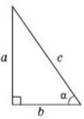
35.   На рисунку зображено прямокутний трикутник з катетами а іb, гіпотенузою с та гострим кутом α. Укажіть правильну рівність. 

 

А)                        Б) cos𝛼=𝑐         В)       Г)      Д)                 ^𝑏

                                                                                                                     𝑐                                        𝑎

                                         

36. 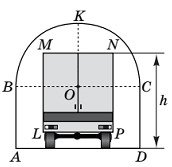  На рисунку зображено поперечний переріз аркового проїзду, верхня частина якого ( дуга ВКС) має форму пів кола радіуса ОС = 2 м. Відрізки АВ і Dc перпендикулярні до AD, АВ =  DC = 2 м. Яке з наведених значень є найбільшим можливим значенням висоти h вантажівки, за якого вона зможе проїхати через цей арковий проїзд, не торкаючись верхньої частини арки ( дуги ВКС)?

Уважайте, що LMNP – прямокутник, у якому MN = 2,4 м і  MN || AD. 

 

А) 4,4 м             Б) 4 м                В) 3,7 м             Г) 3,5 м             Д) 3,2 м

                                                                 

37.   Радіус кола описаного навколо прямокутного трикутнику АВС дорівнює 6,5 см, а один з катетів дорівнює 12 см. Знайдіть площу трикутника АВС.

А) 30 см²                  Б) 32,5 см²         В) 60 см²           Г) 78 см²               Д) 156 см²

                                                                 

38.   Один з катетів прямокутного трикутника дорівнює а, а протилежний до нього кут – α. Визначити радіус кола, описаного навколо трикутника.

 

А) 𝑎   Б) 2𝑎 В) 𝑎    Г) 2𝑎 Д) 𝑎sin𝛼              cos𝛼              2

                                         

39. 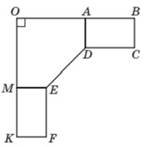  На кресленні кутової шафи ( вид зверху) зображено рівні прямокутники ABCD і KMEF та п’ятикутник EMOAD ( див. рисунок) . Визначте довжину відрізка ED, якщо ОК = ОВ = 1,2 м, КМ = АВ = 0,5 м,  KF = 0,3 м. Укажіть відповідь, найближчу до точної. 

А) 0,5 м             Б) 0,55 м            В) 0,65 м           Г) 0,6 м             Д) 0,7 м

2. Завдання відкритої форми з короткою  відповіддю

 

Розв’яжіть завдання. Одержані відповіді запишіть у відповідному місці.

 

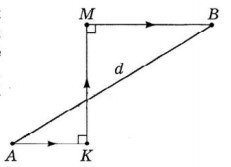
40.             На рисунку зображено траєкторію руху автомобіля з пункту А до пункту В, що складається з трьох прямолінійних ділянок АК, КМ та МВ. Визначте відстань d між пунктами А і В, якщо АК = 60 км, КМ = 120 км, МВ = 100 км (вважайте, що зображені на рисунку відрізки лежать в одній площині). 

 

 

 

41. 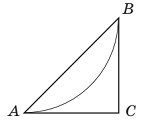            План паркової зони, обмеженої трикутником АВС, зображено на рисунку. Дуга АВ – велосипедна доріжка. Відомо, що дуга АВ є четвертою частиною кола радіуса 1,8 км. СА і СВ – дотичні до цього кола ( А і В – точки дотику) . Обчисліть площу зображеної на плані паркової зони ( у км²). 

 

 

 

42.             У прямокутний трикутник АВС вписано коло, яке дотикається катетів АС і ВС у точках К і М відповідно. Знайдіть радіус кола, описаного навколо трикутника АВС ( у см), якщо АК = 4,5 см, МВ = 6 см.

 

 

43.             Гіпотенуза АС рівнобедреного прямокутного трикутника АВС дорівнює 3,6 м. У цей трикутник вписано квадрат MNKP, дві вершини якого знаходяться на гіпотенузі, а дві інші – на катетах.

1.   Визначте площу трикутника АВС ( у м²).

 

 

2.   Обчисліть площу квадрата MNKP ( у м²).

 

 

44. У прямокутному трикутнику АВС ( ∟С = 90⁰) відстань від середини медіани ВМ до катетів АС і ВС дорівнює 5 см і 6 см відповідно.

1.   Визначте довжину катета АС ( у см).

 

 

2.   Визначте радіус ( у см) кола, описаного навколо трикутника АВС.

 

 

45.    У прямокутному трикутнику  гострий кут дорівнює 60⁰, а бісектриса цього кута – 12 см. Знайдіть більший катет цього трикутнику ( у см).

 

 

46.    У прямокутнику  ABCD, точка К – середина сторони ВС. Відрізок АК =

4 2 см бісектриса кута прямокутника. Визначте площу прямокутника ABCD

( у см² ).

 

 

47.    У прямокутнику  ABCD проведено перпендикуляр АК до діагоналі BD.

Точка К належіть діагоналі BD. АК = 8 см, AD = 4 5 см. Визначте діагональ прямокутника АС ( у см).

 

 

48.    Точка М знаходиться на гіпотенузі АС прямокутного трикутника АВС і на однакової відстані від катетів трикутника. Знайдіть більший катет трикутника ( у см), якщо АМ = 15 см, МС = 20 см.

 

 

Список використаних джерел:

1.      Медяник А.Г. «Учителеві про шкільний курс геометрії». Книга для вчителя/ А. Г. Медяник. - К.: Рад. Шк., 1988. – 124 с.

2.      Тадеєв        В.О.   Геометрія. 7        клас. Поглиблений       курс/

Підручник.В.Тадеєв – «Тернопіль. Навчальна книга – Богдан», 2007. – 352 с. 

3.      Тарасенкова Н.А. «Математика. На допомогу вчителю»/ Н.

Тарасенкова, І. Богатирьова, О. Коломієць, З. Сердюк - Київ. Видавничий дім «Освіта». 2013. – 56 с.

4.      Мерзляк А.Г. Геометрія: підруч. для 8 кл. загальноосвіт. навч.

закладів/  А.Г.Мерзляк, В.Б. Полоський, М.С. Якір – Х.: Гімназія, 2016. – 208 с.: іл.

5.      Мерзляк А.Г. Геометрія: підруч. для 8 кл. загальноосвіт. навч.

закладів з поглибл. вивч. математики /  А.Г.Мерзляк, В.Б. Полоський, М.С.

Якір – Х.: Гімназія, 2016. – 224 с.: іл.

6.      Істер О.С. Геометрія: підруч. для 8 кл. загальноосвіт. навч. закладів/  Істер О.С. – Киів: Генеза, 2016. – 216 с.: іл.

7.      Математика. Комплексна підготовка до ЗНО і ДПА / Уклад.:

А.М.Капіносов [та ін.]. – Тернопіль: Підручники і посібники, 2019 . – 512 с.

8.      Львівський регіональний центр оцінювання якості освіти. Тести ЗНО минулих років. [електронній ресурс]// https://lv.testportal.gov.ua/index.php/testy