Презентація "Тотожні перетворення виразів, що містять квадратні корені"
Про матеріал
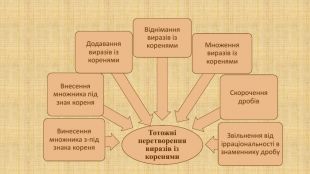
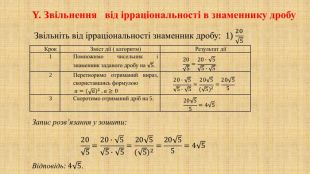
Презентація "Тотожні перетворення виразів, що містять квадратні корені" для здобувачів освіти восьмого класу, які вивчають тему "Тотожні перетворення виразів, що містять квадратні корені". В презентації подано алгоритми і приклади розв'язування вправ на тотожні перетворення виразів, що містять квадратні корені.( для дистанційного навчання) Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку