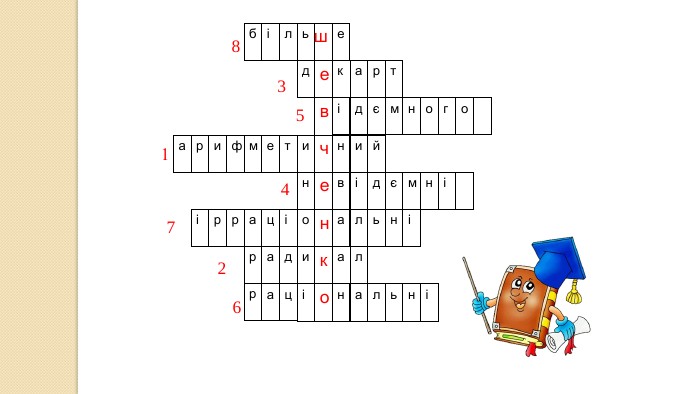
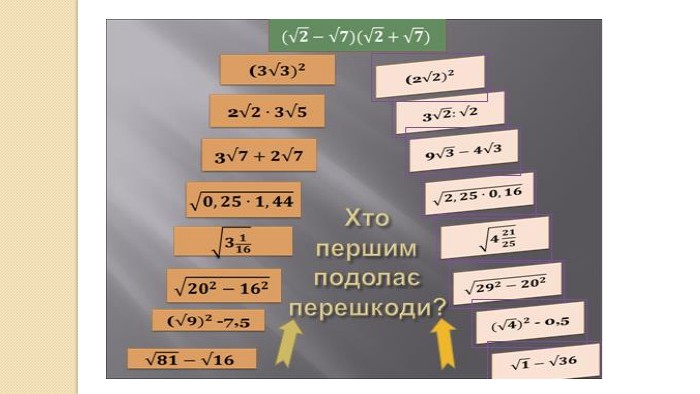
Презентація. Тотожні перетворення виразів, які містять квадратні корені
Про матеріал
Удосконалити вміння виконувати тотожні перетворення виразів, що містять квадратні корені.
Розвивати активність, самостійність, логічне мислення учнів, пізнавальний інтерес до історії математики.
Виховання працьовитості, позитивного ставлення до навчання.
Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку