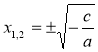Конспект уроку

з  алгебри (8 клас)

 

“ Квадратні рівняння. Неповні квадратні рівняння. ”

 

 

                                                  

 

 

 

 

 

 

 

 

 

                                             

Тема:       Квадратні рівняння. Неповні квадратні рівняння.

Мета уроку: Ввести поняття квадратного рівняння; неповного квадратного рівняння. Ознайомити учнів з методами розв’язування неповних квадратних рівнянь. Навчити застосовувати здобуті знання для розв’язування рівнянь. Формувати навички самостійної роботи. Виховувати критичне ставлення до своєї праці, а також вміння оцінювати свої знання.

  

 

Хід уроку 

1. Організаційний етап.

• привітання;
• перевірка готовності учнів до уроку.

 

2. Перевірка домашнього завдання.

ІІІ.  Актуалізація опорних знань.

Чому дорівнює змінна х?

 

2х=64;      х²=16;     2х²=20;     21х²—х=0.  

 

Із многочленів, записаних на дошці, назвати многочлени другого степеня.

2х+х-7;     3хх-х;     2а-а²+1;     7-bb²;     уу²+2у;     4х²+12х;     9а²—9.

Виберіть серед них ті, які можна розкласти на множники.

Вказати, яким способом можна це зробити.

                                                                              

ІV. Повідомлення теми і мети уроку. Мотивація навчальної діяльності .

Закінчіть речення: 

• Рівність, яка містить невідомі числа, позначені буквами, називається… (рівнянням)
• Невідомі числа в рівнянні називають… (змінними)
• Число, яке задовольняє рівняння, називається його… (коренем або розв`язком)
• Знайти всі корені рівняння або показати, що їх не існує, означає… (розв`язати рівняння)
• Рівняння виду ах=b, де а і b—дані числа, називається… (лінійним рівнянням)
• Числа а і b--…(коефіцієнти)
• Число b--…(вільний член)

 

 

 

V. Вивчення нового матеріалу.

      

Квадратним  рівнянням називається рівняння виду   ах²+ bх + с = 0 (1),

   де х – змінна,  а, b і с – деякі числа,   причому а ≠ 0.

  Числа а, b і с – коефіцієнти квадратного рівняння.

  (а – перший коефіцієнт, b – другий коефіцієнт, с – вільний член).

   Наприклад,   – х²+ 6х + 1,4 = 0;    8х²– 7х = 0.

   Якщо а = 1, то квадратне рівняння (1) називається зведеним.

   Якщо в квадратному рівнянні aх² + bx + c = 0, хоча б один із коефіцієнтів b i c = 0, то такі рівняння називаються неповними квадратними рівняннями.

                                                                                                                          

Класифікація неповних квадратних рівнянь

Неповні квадратні рівняння
b = 0, ах2 + с = 0, ах2 = – с, . Якщо  ,       два  корені: Якщо  ,  немає коренів.	c = 0, ax2 + bx=0 х(ах + b) = 0, x = 0 або aх + b = 0.  два корені: x 1= 0,	с = b = 0, ах2 = 0 один корінь х = 0

 

              Історична довідка.

Квадратні рівняння простіших видів вавилонські математики вміли розв’язувати ще 4 тис. років тому. Згодом розв’язували їх також в Китаї та Греції. Особливо багато уваги квадратним рівнянням приділив Мухаммед аль-Хорезмі (ІХ ст.)

    Займалися розв’язуванням квадратних рівнянь Омар Хайям і Рене Декарт,

      Евклід і Діофант.

                                                                                                              

 

 

 

Франсуа Вієт.

Французького математика Вієта називають «батьком алгебри». Він першим почав позначати буквами не лише змінні, а й коефіцієнти. Це дало можливість узагальнити способи розв’язування рівнянь, скласти алгоритм розв’язування.   Вієт знайшов загальні способи розв’язування рівнянь 2-го, 3-го, 4-го степенів. Для розв’язування зведених квадратних рівнянь застосовують теорему Вієта.

                                                                                                    

VI.  Первинне закріплення  вивченого матеріалу.

Усні вправи.

1.Чи є квадратним рівняння? Якщо так, то вкажіть його коефіцієнти:

 

а) 3,7х² – 5х + 1 = 0;

б) 48х² – х³– 9 = 0;

в) 2,1х² + 2х – 0,728 = 0;

г) 1 – 12х = 0;

ґ) 7х² – 13 = 0;

д) – х² = 0?

                                                                                                                               

 

2.Укажіть, які з даних рівнянь є зведеними, і перетворіть незведені рівняння у зведені:

 

а) 5х² – 9 х + 4 = 0;

б) х² + 3х – 10 = 0;

в) – х² – 8х + 1 = 0;

г) 6х² – 30х = 0;

ґ) 9х² = 0.

 

3. Розв‘яжіть рівняння:                                      

а) 2х² – 72 = 0.            Відповідь: -6; 6.                                             

б) 5х²– 8х = 0.            Відповідь: 0; 1,6.                                                             

в) х² + 121 = 0.           Відповідь: коренів немає .                                                

г) 25х² – 16 = 0.       Відповідь: -0,8; 0,8.  

 

Робота з підручником ( Мерзляк А.Г. та ін. “Алгебра” 8 клас,  2016 р.)

№ 592, 601, 603.

VII. Підсумок  уроку.

1. Виконання тестових завдань.

1. Укажіть рівняння, яке є квадратним:

а) 5х² – х + 3 = 0;

б) 5х² – х³ + 3 = 0;

в) 8х + 1 = 0;

г) – 30х = 0.

 

2. Рівняння називають неповним, коли (відповідей може бути декілька):

а) b ≠ 0, c = 0;

б) a = 0, b ≠0, c ≠ 0;

в) b = 0, c ≠ 0;

г) b = c = 0.

                                                                                                               

3. У квадратному рівнянні ах² +bх + с = 0, числа a і b називають:

а) многочлени;

б) коефіцієнти;

в) вільні члени;

г) квадратні степені.

                                                                                                            

 

 

 

2. Рефлексія.

Закінчіть речення.

Сьогодні на уроці:

• навчився (навчилася)…
• зрозумів (зрозуміла)...

 

 

VІІI. Домашнє завдання.

 

§ 18, № 602, 606.  ( Мерзляк А.Г. та ін. “Алгебра” 8 клас,  2016 р.)

 

 

 

IX. Оцінювання знань учнів.