Презентація "Третя ознака рівності трикутників"
Про матеріал
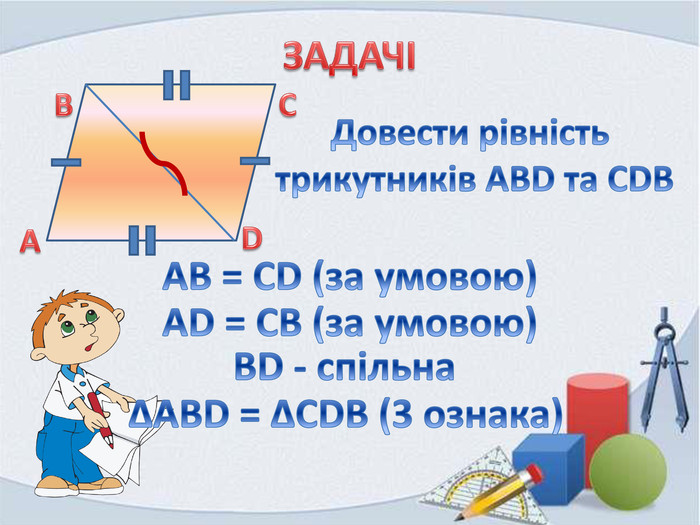
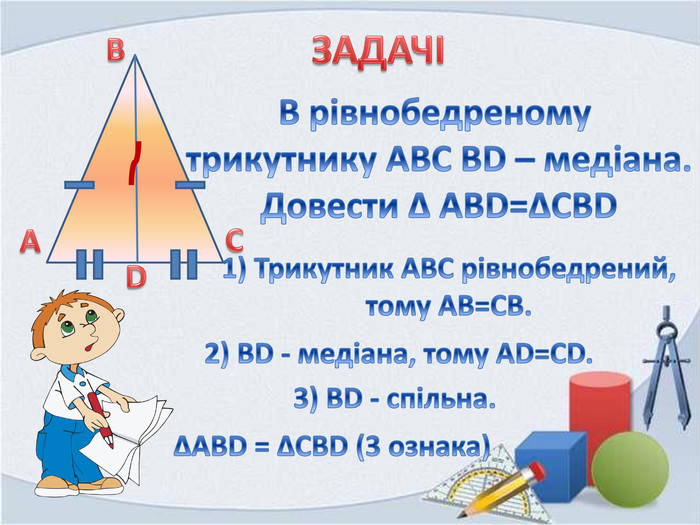
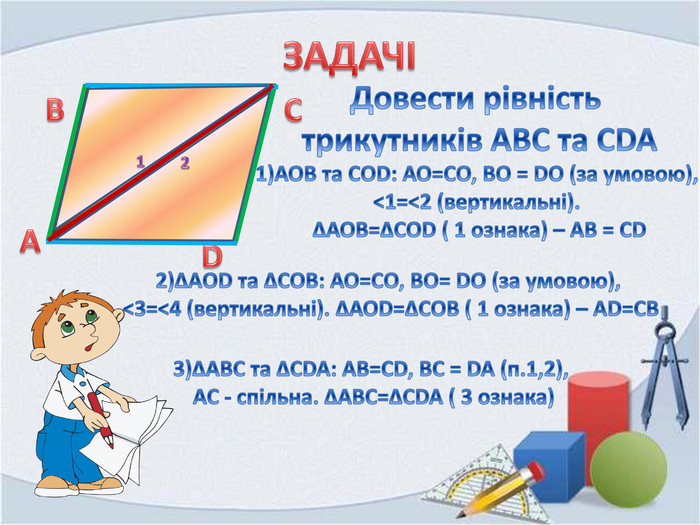
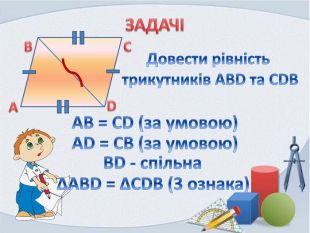
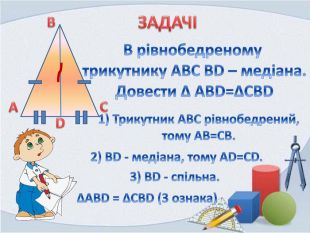
В презентації розглянуті вправи на закріплення раніше вивченого матеріалу, подається формулювання третьої ознаки рівності трикутників та розглядаються задачі на застосування цієї ознаки Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку




















-

Кравченко Лілія
29.01.2024 в 15:00
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Мирошниченко Зоя Михайлівна
18.01.2024 в 07:26
Дякую
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Гостєва Ольга Володимирівна
11.12.2023 в 21:03
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Вигоднер Діана Ісаківна
05.12.2023 в 21:21
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Mартиняк Оксана Семенівна
18.01.2023 в 22:47
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Левадній Сергій Павлович
15.01.2023 в 14:50
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Андрейченко Тетяна Олексіївна
06.12.2022 в 21:58
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Константинова Олена Павлівна
27.11.2022 в 00:57
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Kr Elena
23.01.2022 в 15:33
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 6 відгуків