Презентація Тригонометричні функції






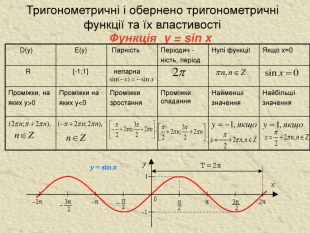
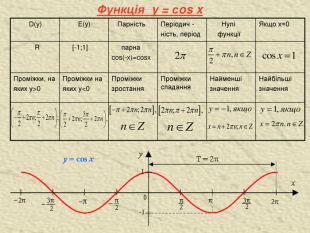
![Функція y = sin x Найбільші значення Найменші значення Проміжки спадання Проміжки зростання Проміжки на яких у<0 Проміжки, на яких у>0 непарна [-1;1] R Якщо х=0 Нулі функції Періодич - ність, період Парність E(y) D(y) Тригонометричні і обернено тригонометричні функції та їх властивості Функція y = sin x Найбільші значення Найменші значення Проміжки спадання Проміжки зростання Проміжки на яких у<0 Проміжки, на яких у>0 непарна [-1;1] R Якщо х=0 Нулі функції Періодич - ність, період Парність E(y) D(y) Тригонометричні і обернено тригонометричні функції та їх властивості](/uploads/files/461847/112280/119828_images/9.jpg)
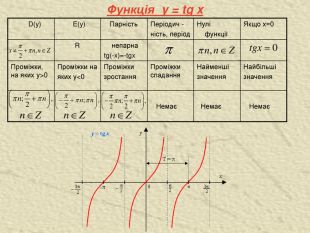
![Найбільші значення Найменші значення Проміжки спадання Проміжки зростання Проміжки на яких у<0 Проміжки, на яких у>0
парна cos(-x)=cosx [-1;1] R Якщо х=0 Нулі функції Періодич - ність, період Парність E(y) D(y) Функція y = сos x Найбільші значення Найменші значення Проміжки спадання Проміжки зростання Проміжки на яких у<0 Проміжки, на яких у>0
парна cos(-x)=cosx [-1;1] R Якщо х=0 Нулі функції Періодич - ність, період Парність E(y) D(y) Функція y = сos x](/uploads/files/461847/112280/119828_images/10.jpg)


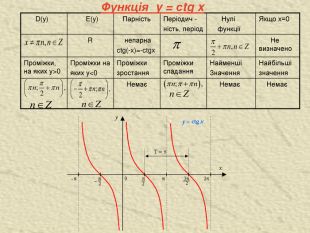
![Функція y = arcos x Арккосінусом числа називають таке число з проміжку , косинус якого дорівнює . Основні властивості функції D(y)=[-1;1]. 2. 3. Графік не симетричний ані відносно початку координат, ані відносно осі OY: 4. Функція спадна. Якщо то 5. y=0, якщо x=1. 6. Функція y=cos x спадає на відрізку і набуває всіх значень від -1 до 1, тому рівняння на проміжку має єдиний корінь, який називають арккосинусом числа і позначають arccos . Функція y = arcos x Арккосінусом числа називають таке число з проміжку , косинус якого дорівнює . Основні властивості функції D(y)=[-1;1]. 2. 3. Графік не симетричний ані відносно початку координат, ані відносно осі OY: 4. Функція спадна. Якщо то 5. y=0, якщо x=1. 6. Функція y=cos x спадає на відрізку і набуває всіх значень від -1 до 1, тому рівняння на проміжку має єдиний корінь, який називають арккосинусом числа і позначають arccos .](/uploads/files/461847/112280/119828_images/14.jpg)



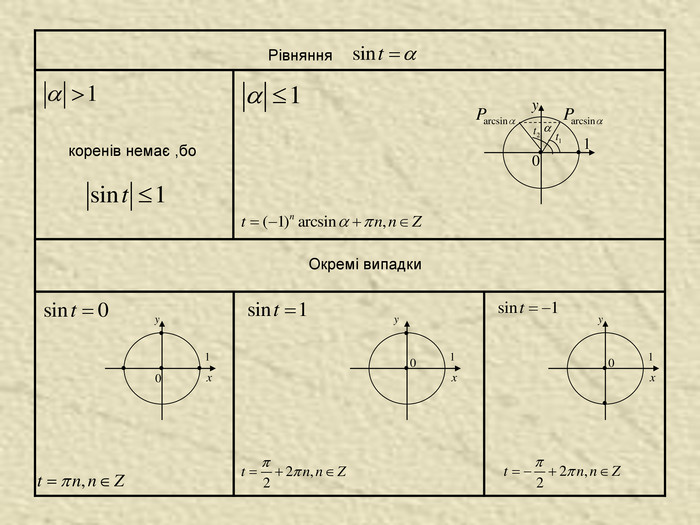



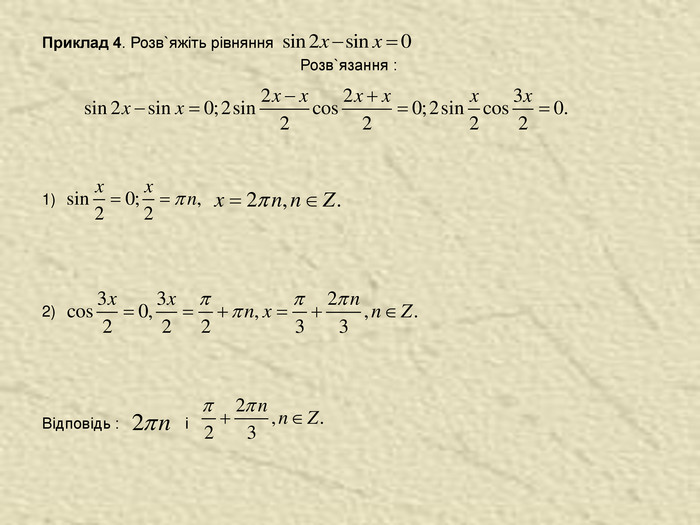

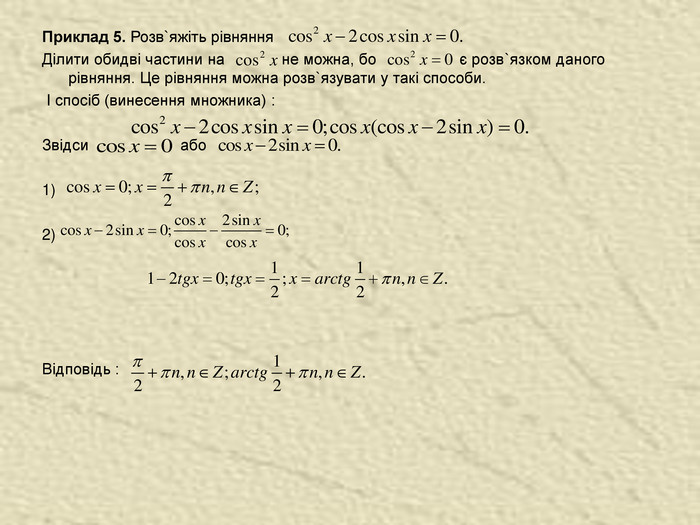



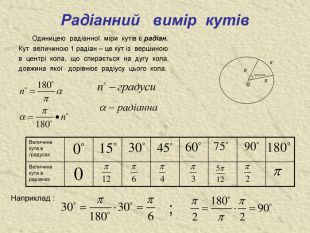
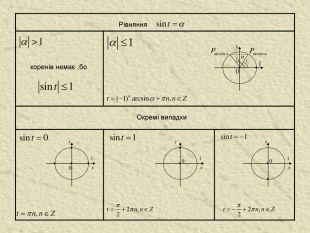
вісь синусів вісь косинусів вісь котангенсів вісь тангенсів Означення синуса, косинуса, тангенса і котангенса. Синусом числа називають ординату точки , утвореної поворотом точки (1;0) навколо початку координат на кут радіан ( позначають sin ). Синус визначено для будь-якого числа . Косинусом числа називають абсцису точки ,утвореної поворотом точки (1;0) навколо початку координат на кут радіан ( позначають cos ). Косинус визначено для будь-якого числа . Тангенсом числа називають відношення синуса числа до його косинуса. Котангенсом числа називають відношення косинуса числа до його синуса.
Функція y = sin x Найбільші значення Найменші значення Проміжки спадання Проміжки зростання Проміжки на яких у<0 Проміжки, на яких у>0 непарна [-1;1] R Якщо х=0 Нулі функції Періодич - ність, період Парність E(y) D(y) Тригонометричні і обернено тригонометричні функції та їх властивості
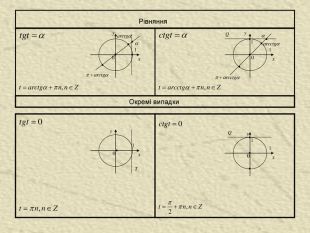
Функція y = arsin x Означення та основні властивості обернених тригонометричних функцій Функція у=sin х зростає на проміжку і набуває всіх значень від -1 до 1, тобто кожного свого значення функція набуває в єдиній точці області визначення. Арксинусом числа називають таке число з проміжку , синус якого дорівнює . Основні властивості функції y=arcsinx: 1. 2. 3.Графік симетричний відносно початку координат (функція непарна) : arcsin (-x)=-arcsin x. 4. Функція зростаюча. Якщо то 5. y=0, якщо x=0. 6.
Функція y = arcos x Арккосінусом числа називають таке число з проміжку , косинус якого дорівнює . Основні властивості функції D(y)=[-1;1]. 2. 3. Графік не симетричний ані відносно початку координат, ані відносно осі OY: 4. Функція спадна. Якщо то 5. y=0, якщо x=1. 6. Функція y=cos x спадає на відрізку і набуває всіх значень від -1 до 1, тому рівняння на проміжку має єдиний корінь, який називають арккосинусом числа і позначають arccos .
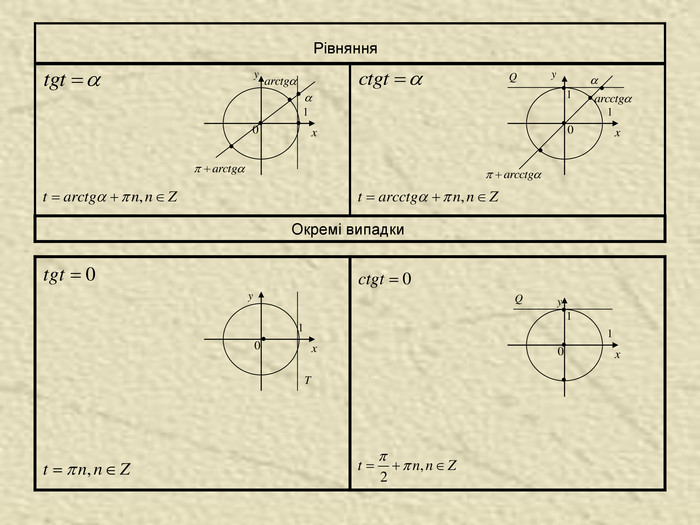
Функція y = arctg x Функція y=tg x на проміжку зростає і набуває всіх значень із R, тому для будь-якого рівняння має єдиний корінь із проміжку який називають арктангенсом числа і позначають Арктангенсом числа називають таке число з проміжку тангенс якого дорівнює Основні властивості функції 1. D(y)=R. 2. 3. Графік симетричний відносно початку координат, функція непарна: 4. Функція зростаюча. Якщо 5. y=0,якщо x=0. 6. y>0,якщо x>0;y<0, якщо x<0.
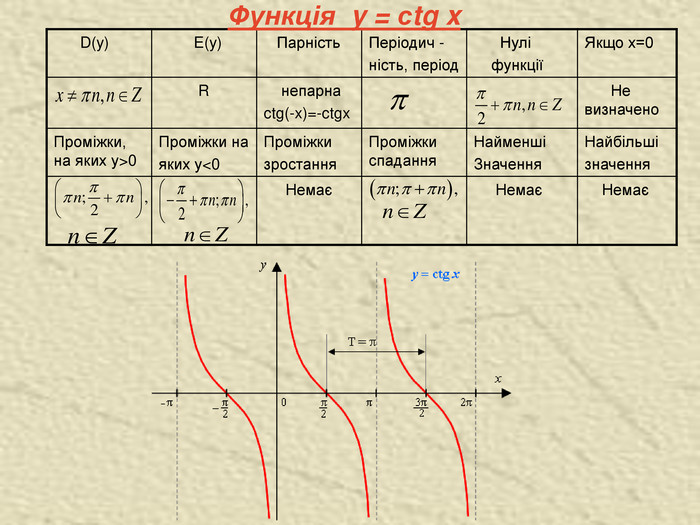
Функція y = arcctg x Функція y=ctgx на інтервалі спадає і набуває всіх значень із R, тому для будь-якого числа в інтервалі існує єдиний корінь рівняння Це число називають арккотангенсом числа позначають Арккотангенсом числа називають таке число з інтервалу котангенс якого дорівнює Основні властивості функції y=arcctgx: 1. D(y)= R. 2. E(y)= 3. Графік не симетричний ані відносно початку координат, ані відносно осі OY: 4. Функція спадна. Якщо 5. x=0, якщо 6. y > 0 для всіх
Методи розв`язування тригонометричних рівнянь Тригонометричні рівняння можна привести шляхом тотожних перетворень до рівнянь з однією тригонометричною функцією, потім зробити заміну і привести рівняння до алгебраїчного. Розглянемо приклади : Приклад 1. Розв`яжіть рівняння Розв`язання Замінивши на маємо : Нехай х = t, тоді Звідси Оскільки то розв`язків немає. Оскільки то Відповідь :
Зведення тригонометричних рівнянь до рівнянь виду Багато тригонометричних рівнянь, права частина яких дорівнює 0, розв`язуються розкладанням їхньої лівої частини на множники. Приклад 3. Розв`яжіть рівняння Розв`язання Урахувавши,що маємо : Добуток дорівнює нулю, якщо хоча б один із множників дорівнює нулю. Тому: 1) 2) Відповідь:
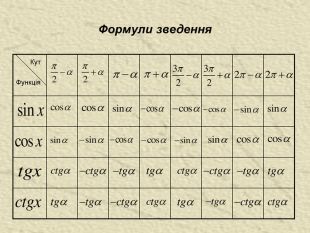
Однорідні тригонометричні рівняння Рівняння виду asin x + bcos x = 0 (однорідне рівняння 1-го степеня), де a i b не дорівнюють нулю. Значення x, при яких cos x дорівнює нулю, не задоволюняє даному рівнянню, бо тоді й sin x також дорівнював би нулю, а cos x і sin x не можуть одночасно дорівнювати нулю. Тому Рівняння виду називається однорідним рівнянням 2-го степеня. Ділимо на Розв`язавши отримане рівняння, одержимо корені даного рівняння.


про публікацію авторської розробки
Додати розробку














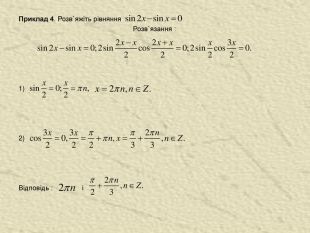




-

Зеніна Світлана Савеліївна
02.04.2023 в 15:02
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Дяченко Світлана Михайлівна
06.03.2023 в 22:15
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Новомлинська Дар'я Сергіївна
03.11.2022 в 11:29
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Головко Наталя Василівна
06.09.2022 в 20:26
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 1 відгук