Презентація з теми "Аксіоми стереометрії та наслідки з них"
Про матеріал
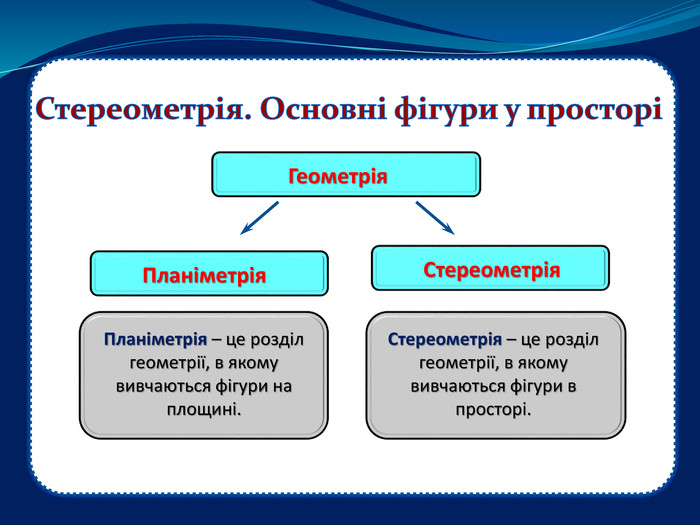
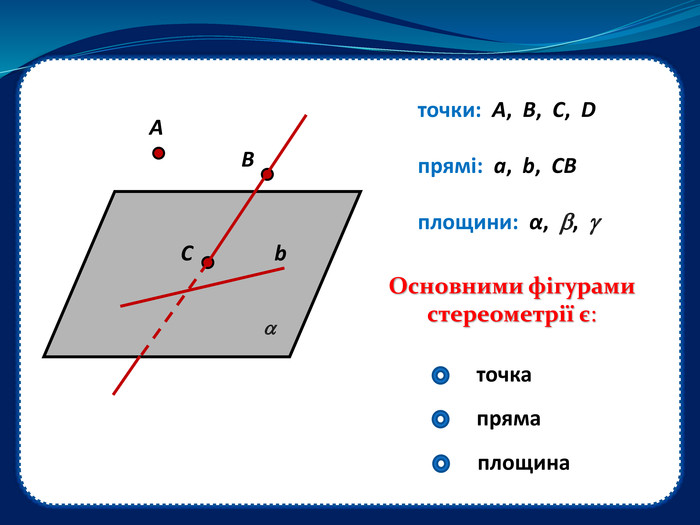
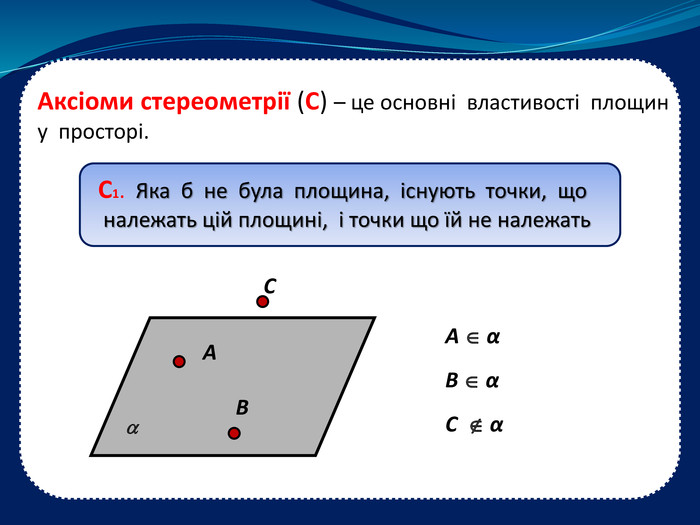
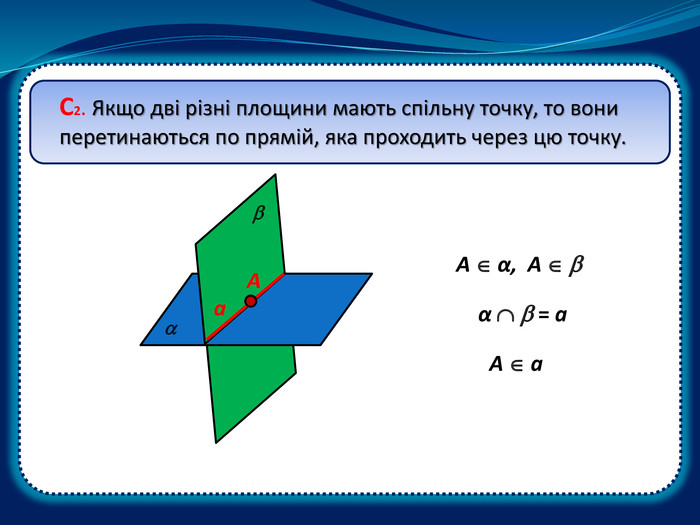
Дана презентація , як пояснювально-ілюстративний метод навчання, допоможе вчителю організувати засвоєння учнями інформації з даної теми та забезпечити успішне сприйняття нового матеріалу, формувати в учнів систему образного мислення. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку













-

Маренич Неля
08.09.2025 в 23:20
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Kosyhina Elena
01.12.2023 в 11:05
Щиро дякую за матеріал!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Сердюк Людмила Миколаївна
13.10.2023 в 16:25
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
-

Воробйова Лариса Вячеславівна
25.09.2023 в 20:41
Коротко, чітко, яскраво, гарно сприймається.Основа, необхідна для розв'язування задач. Дякую!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Г.С. Шинкаренко
25.09.2023 в 08:17
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Андрейченко Тетяна Олексіївна
10.04.2023 в 22:20
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Якименко Оксана Вікторівна
11.10.2022 в 21:09
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Горстка Валентина Георгіївна
06.10.2022 в 23:08
Дякую, молодець
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Матвій Галина
14.09.2022 в 22:26
Коротко, чітко сформульовано основу теорію необхідну для розв'язування задач. Дякую)
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Квітко Світлана Миколаївна
07.09.2022 в 20:05
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Волошина Наталія
07.09.2022 в 10:58
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Мисік Марина Олександрівна
05.09.2022 в 15:12
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Жиляк Елеонора Володимирівна
04.09.2022 в 19:36
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Прошак Сергій Володимирович
31.08.2022 в 18:20
Щиро дякую!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кривонос Любов Петрівна
27.08.2022 в 21:32
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Карамян Маргарита
21.09.2021 в 02:04
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Асламова Любов Володимирівна
18.01.2021 в 23:56
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
Показати ще 14 відгуків