Презентація "Тригонометричні функції числового аргументу"
Про матеріал
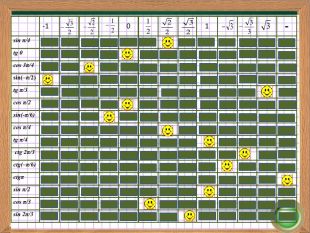
Забезпечити повторення, узагальнення і систематизацію матеріалу теми, подовжити формувати вміння й уміння з використання тригонометричних формул, створити умови контролю Перегляд файлу
Зміст слайдів

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку