Презентація Тригонометричні рівняння і історія розвитку тригонометріі ( окремі факти)
Про матеріал
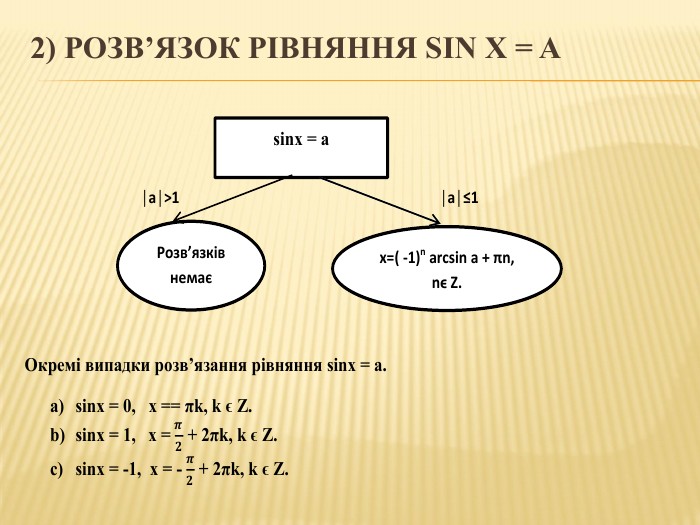
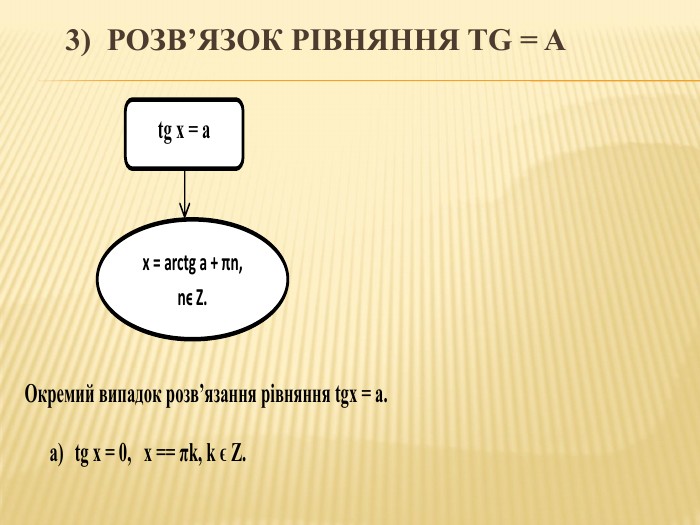
Презентація до уроку " Розв'язування тригонометричних рівнянь" з теми " Тригонометричні рівняння і нерівності". Перегляд файлу
Зміст слайдів

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку