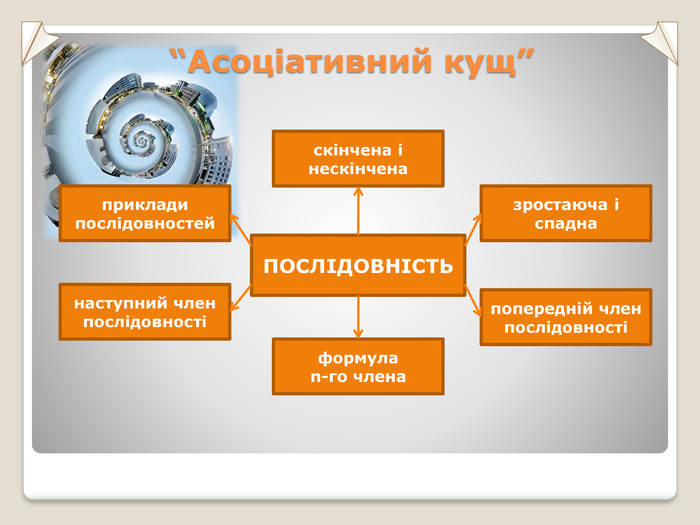
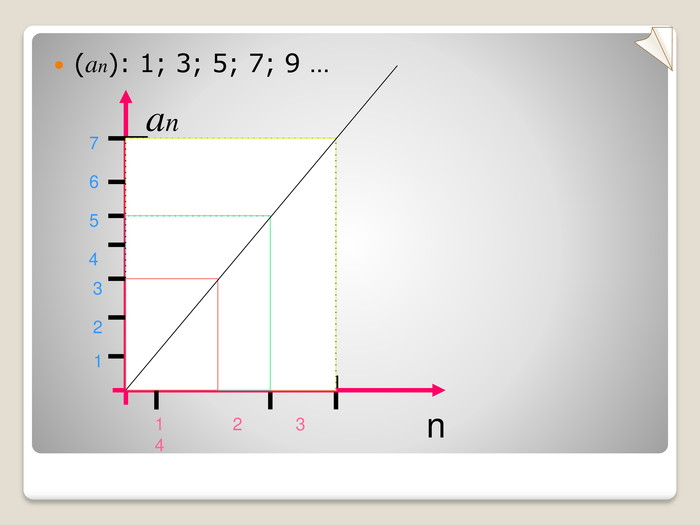
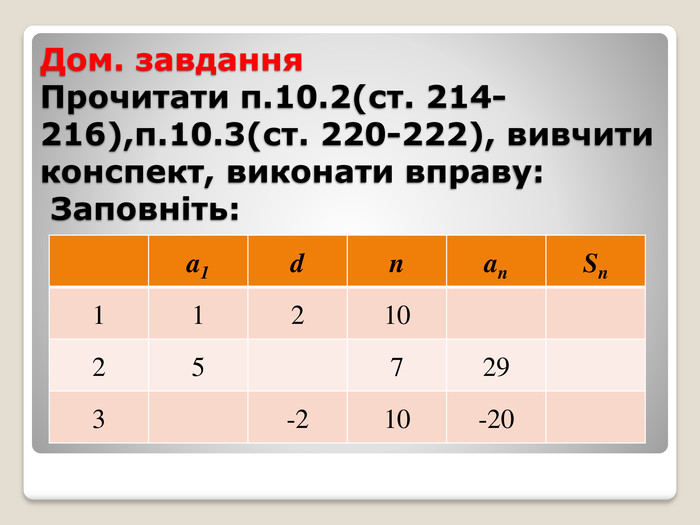
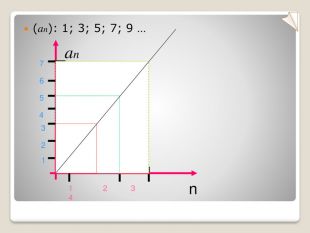
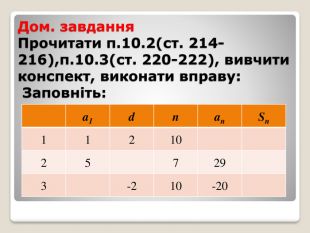
Презентація. Урок-лекція алгебра, 9 клас Арифметична прогресія, її властивості. Формула n-го члена арифметичної прогресії. Сума n перших членів арифметичної прогресії

“Асоціативний кущ”ПОСЛІДОВНІСТЬскінчена інескінченаприклади послідовностейзростаюча і спаднанаступний член послідовностіпопередній член послідовностіформула n-го члена

«Арифметична прогресія, її властивості. Формула n-го члена арифметичної прогресії. Сума n перших членів арифметичної прогресії»style.colorfillcolorfill.type

Мета: сформувати означення арифметичної прогресії, сформувати поняття n-го члена арифметичної прогресії, поняття суми n перших членів арифметичної прогресії, розвивати вміння аналізувати, систематизувати, застосовувати теоретичні відомості для розв’язування вправ; виховувати інтерес до знань, до роботи з комп’ютерною технікою.style.colorfillcolorfill.type

План лекції 1. Означення арифметичної прогресії.2. Формула n-го члена арифметичної прогресії.3. Історична довідка. 4. Характеристична властивість прогресії. 5. Сума n перших членів арифметичної прогресії. 6. Графічне задання арифметичної прогресії.

Поняття арифметичної прогресіїРозглянемо числові послідовності та звернемо увагу на їх особливості:а) 7; 10; 13; 16; 19;(а — діаметри шківів (у см), насаджених на спільний вал). Кожен член цієї послідовності, починаючи з другого, можна отримати, додавши до попереднього члена число 3. б) 6; 4,5; 3; 1,5; 0; -1,5; ... У послідовності кожен член, починаючи з другого, можна отримати, віднявши 1,5 від попереднього члена (або додавши до попереднього члена -1,5). Такі послідовності називають арифметичною прогресією.

Поняття арифметичної прогресіїЧислова послідовність, кожний член якої, починаючи з другого, дорівнює попередньому членові, до якого додають одне і те саме число, називається арифметичною прогресією.Інакше кажучи, числова послідовність a1 , a2 , а3, ..., аn, ... є арифметичною прогресією, якщо для будь-якого натурального числа n виконується умова an+1 = a n + d. З цієї рівності випливає рівність an+1 - a n = d яка означає, що різниця між будь-яким наступним і попереднім членами арифметичної прогресії дорівнює одному і тому самому числу, яке тому і називають різницею прогресії (d). Якщо різниця прогресії d > 0, то прогресія є зростаючою, якщо різниця d < 0, то прогресія є спадною, а при d = 0 — сталою.

Поняття арифметичної прогресіїПриклад 1.прогресія 20; 24; 28; ... є зростаючою (d = 4 > 0);Приклад 2.прогресія 11; 8; 5; ... є спадною (d = -3 < 0);Приклад 3.прогресія 2; 2; 2; ... є сталою (d = 0).

Випишіть перші п’ять членів арифметичної прогресії (an ), якщо:а) a1 = 10, d = 4; б) a1 = 1,7, d = -0,2.а) a2 =a1 + d=10+4=14;a3 =a2 + d= 14+4=18;a4 =a3 + d= 18+4=22;a5 =a4 + d= 22+4=26. Відповідь: 10; 14; 18; 22; 26.б) a2 =1,7+(-0,2)=1,5;a3 =1,5 +(-0,2)= 1,3;a4 =1,3 +(-0,2)= 1,1;a5 =1,1 +(-0,2)= 0,9. Відповідь: 1,7; 1,5; 1,3; 1,1;0,9.

Формула загального члена арифметичної прогресії аn = а1 + (n-1)d. З означення арифметичної прогресії випливає:а2 = а1 + d а3 = а2 + d=(а1 + d)+d =а1+2d;а4 = а3 + d=(а1 +2d)+d=a1+3d;а5 = а4 + d=(а1 +3d)+d=а1+4d і т.д. Аналізуючи здобуті формули, помічаємо, що відповідний член прогресії отримують додаванням до першого її члена а1 різниці прогресії d, помноженої на число, яке на 1 менше від порядкового номера шуканого члена. Поширюючи за аналогією цей висновок на наступні члени , можемо записати, що аn = а1 + (n-1)d. Таким чином, ми отримали формулу загального члена арифметичної прогресії.

Усна вправа. Виразіть, користуючись формулою :

Формула загального члена арифметичної прогресії аn = а1 + (n-1)d. Приклад 1. Знайти 7-й член арифметичної прогресії (аn), якщо а1= 9, d=-2. Розв'язання. а7 = а1 + 6d = 9 + 6  (-2) = -3; Відповідь: а7 = -3. Приклад 2. Знайти перший член арифметичної прогресії (аn), якщо її п'ятий член дорівнює 12, а різниця становить 4. Розв'язання. а5 = a1 + 4d; 12 = а1 + 4  4; а1 = 12 - 16 = -4; Відповідь: а1 = -4.

Сума двох членів скінченої арифметичної прогресії, рівновіддалених від її кінців, дорівнює сумі крайніх членів

Формуласуми першихn членів арифметичної прогресії:

Користуючись формулою знайти суму перших двадцяти членів арифметичної прогресії 5, 7, 9,…. Розв’язання:a1 = 5; n = 20.d = 7 – 5 = 2;a20 = а1 + 19 d = =5 + 19 · 2 = 43 Відповідь: 480.

(an): 1; 3; 5; 7; 9 …nan1 2 3 47654321style.colorfillcolorfill.typefill.onrrrrr

Підведемо підсумки. Арифметична прогресія- числова послідовність, кожний член якої, починаючи з другого, дорівнює попередньому членові, до якого додають одне і те саме число - різниця арифметичної прогресії (число)

Підведемо підсумки. Формула n-го члена арифметичної прогресіїВластивість n-го члена арифметичної прогресіїСума двох членів скінченої арифметичної прогресії, рівновіддалених від її кінців, дорівнює сумі крайніх членів

Підведемо підсумки. Формула суми n перших членів арифметичної прогресії

Дом. завдання. Прочитати п.10.2(ст. 214-216),п.10.3(ст. 220-222), вивчити конспект, виконати вправу: Заповніть:{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}a1dnan. Sn11210257293-210-20

Правило для знаходження суми членів арифметичної прогресії дається у «Книзі абака» (1202 р.) італійського вченого-математика Леонардо Фібоначчі. Правило для суми скінченної геометричної прогресії зустрічається у книзі Н. Шюке «Наука про числа», яка побачила світ у 1484 році. Наука про числа. Цікаво знати

Арифметична прогресія. Формула n-го члена арифметичної прогресії

Формула загального члена арифметичної прогресії аn = а1 + (n-1)d. Приклад 3. Знайти перший член і різницю арифметичної прогресії (аn), якщо а6 = 18 і а11 = З0. Розв'язання. Знайдемо d.а6 = а1 + 5d, a11 = а1 + 10d;a11 - а6 = (а1 + 10d ) - (а1 + 5d) = 5d; 30-18 =5d,d = 2,4 Знайдемо а1 :а6 = а1 + 5d 18 = а1 + 52,4;18 = а1 + 12; а1 =18 - 12 = 6;a1 = 6. Відповідь. a1 = 6, d = 2,4.

Запитання для самоперевірки. Яку числову послідовність називають арифметичноюпрогресією?Що таке різниця арифметичної прогресії?Як обчислити будь-який член арифметичної прогресії,знаючи її перший член і різницю?Чи правильне твердження: арифметичну прогресіюможна задати її першим членом і різницею прогресії?Чи правильне твердження: арифметичну прогресіюзадають будь-які два її члени?