Презентація .Вектори в просторі. Дії над векторами
Про матеріал
Презентація до уроку геометрії 10 класу «Вектори у просторі. Дії над векторами.»
Зміст :
Повторення
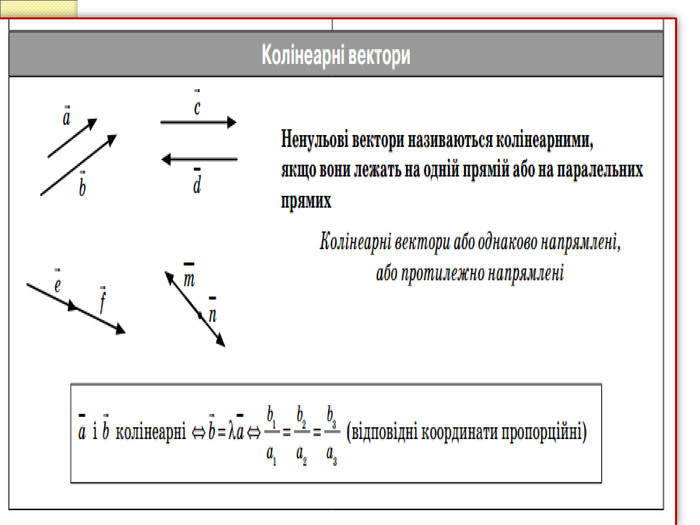
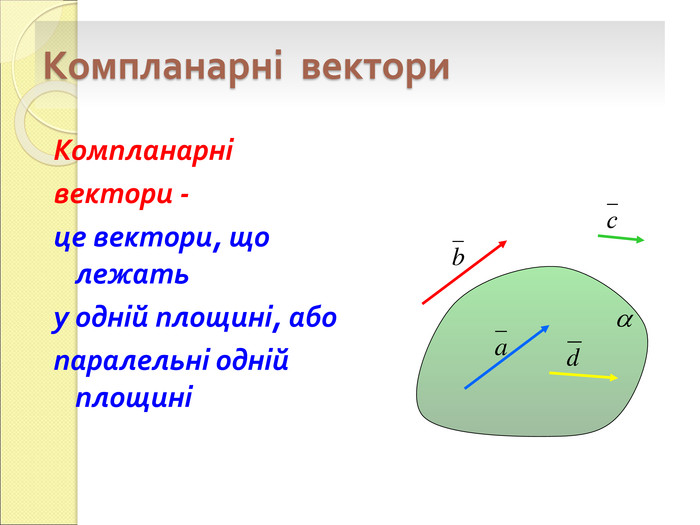
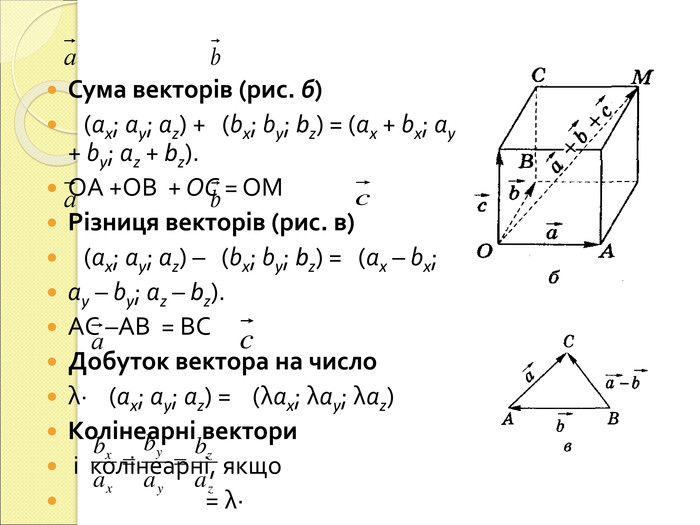
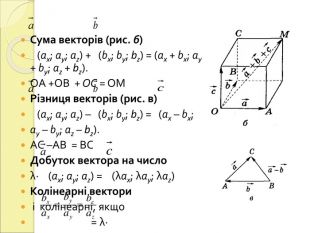
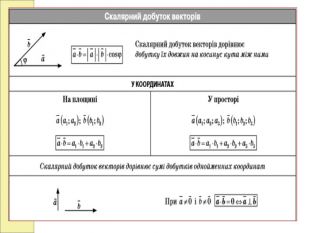
1.Поняття вектора у просторі.
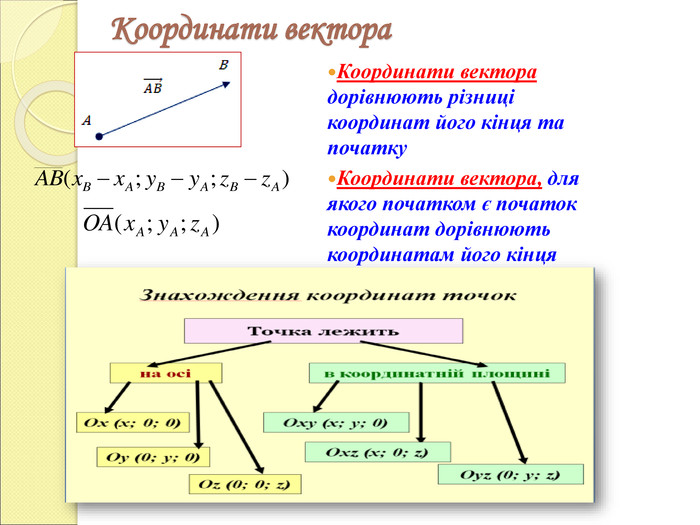
2.Координати вектора у просторі.
3.Абсолютна величина вектора у просторі.
4.Рівні вектори у просторі.
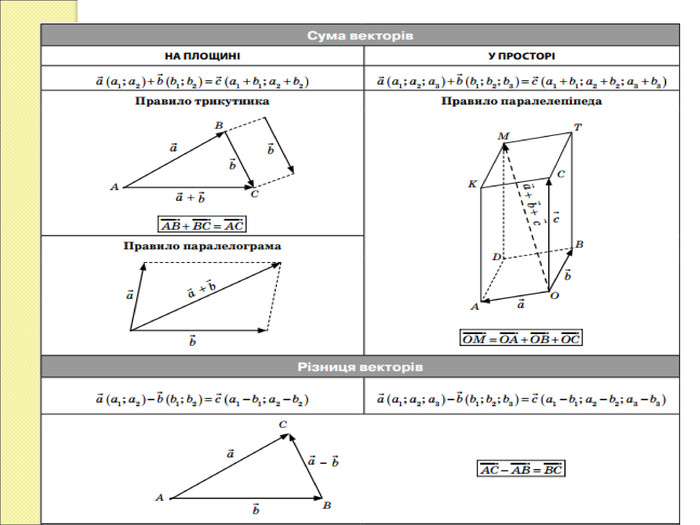
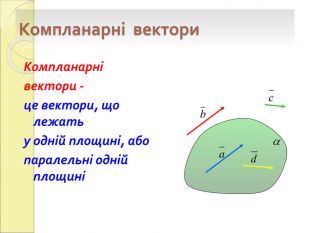
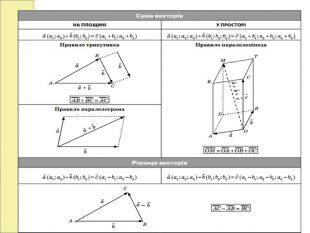
Вивчення нового матеріалу «.Дії над векторами у просторі»
Розв’язання задач на « Дії над векторами у просторі»
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
Оцінка розробки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку


































-

Клепікова Ольга Анатоліївна
21.05.2024 в 22:58
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Г.С. Шинкаренко
15.04.2024 в 01:30
Загальна:
4.7
Структурованість
4.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Сологуб Ольга Юріївна
11.12.2023 в 18:18
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Левадній Сергій Павлович
13.04.2023 в 15:30
Гарно!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Ольга Носальська
03.04.2023 в 23:16
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Стецько Олександра Іванівна
10.03.2023 в 11:43
Дякую
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Шелег Галина Миколаївна
22.04.2022 в 11:16
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 4 відгука