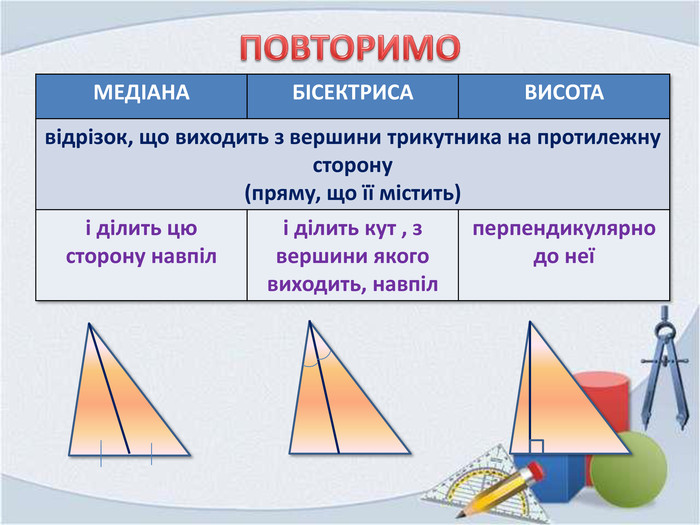
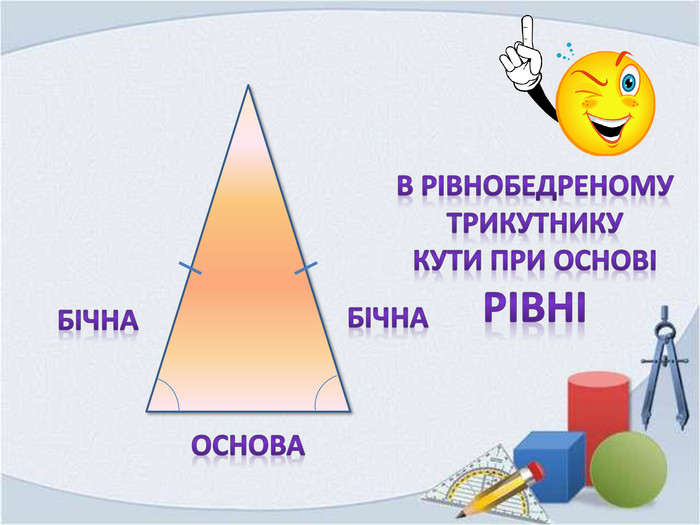
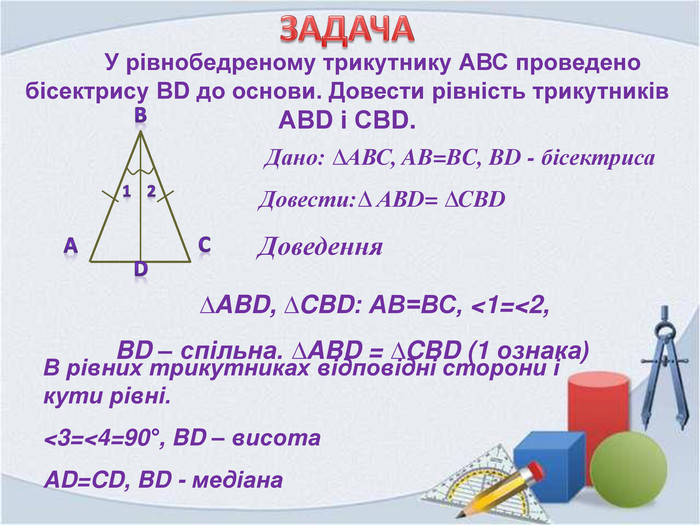
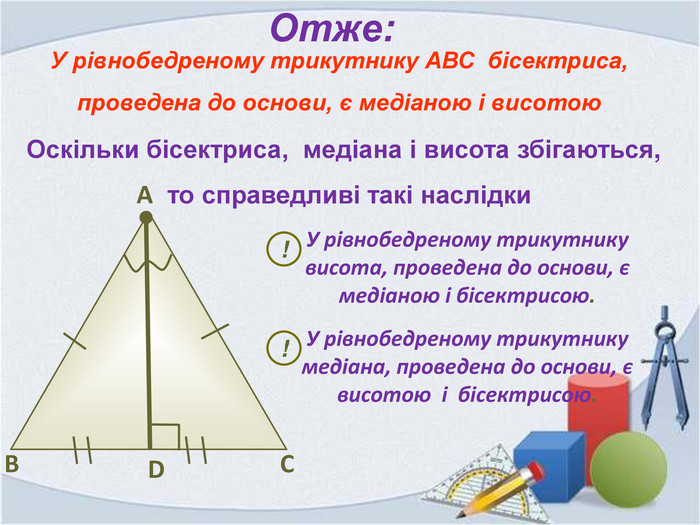
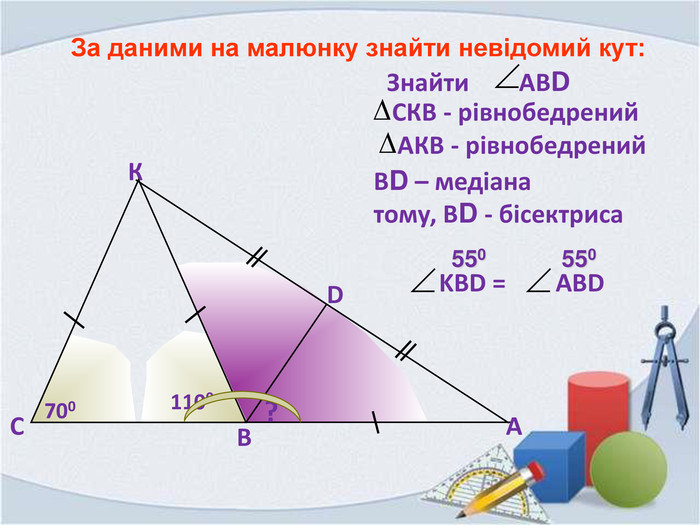
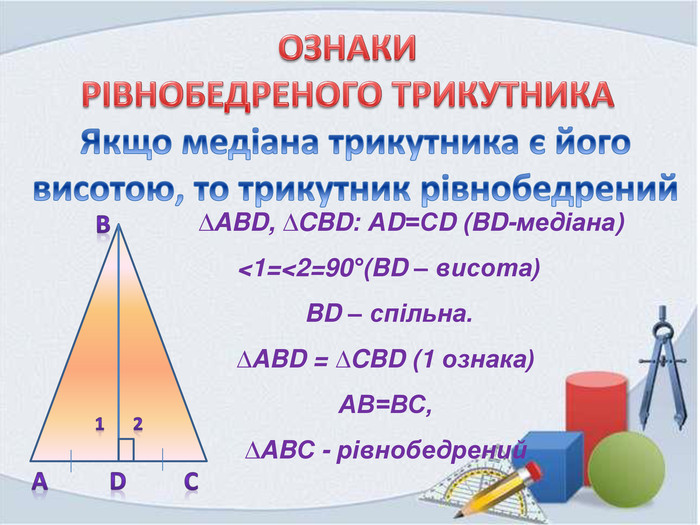
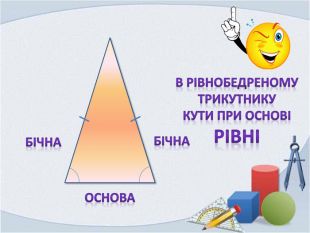
Презентація "Властивість бісектриси рівнобедреного трикутника"
Про матеріал
Презентація складена до вивчення теми "Властивість бісектриси рівнобедреного трикутника". Вона супроводжує урок від закріплення раніше вивчених понять до розв'язування задач із застосуванням нового матеріалу Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Чудові анімаційні ефекти і подача матеріала!
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку