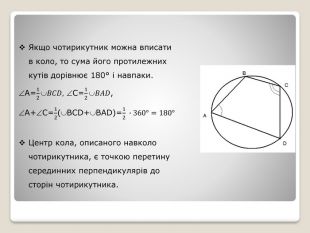
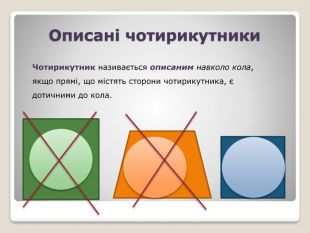
Презентація "Вписані та центральні кути. Вписані та описані чотирикутники."
Дана презентація розроблена до навчального предмету «Геометрія» 8 клас до теми «Чотирикутники» згідно навчальної програми з математики для загальноосвітніх навчальних закладів затвердженої Наказом Міністерства освіти і науки України від 07.06.2017 № 804.
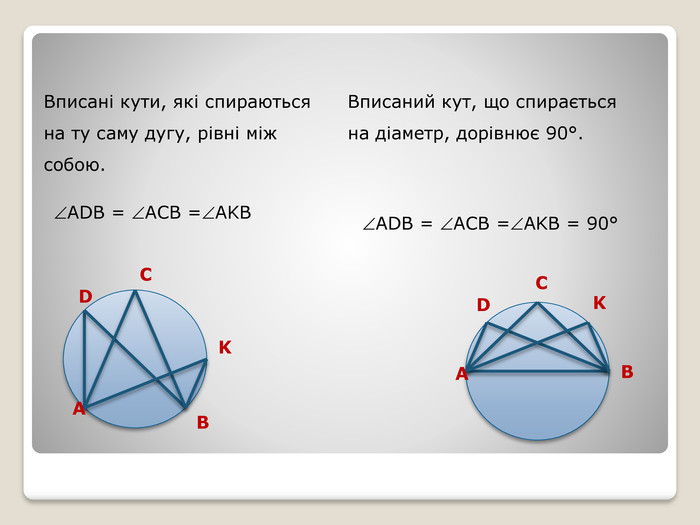
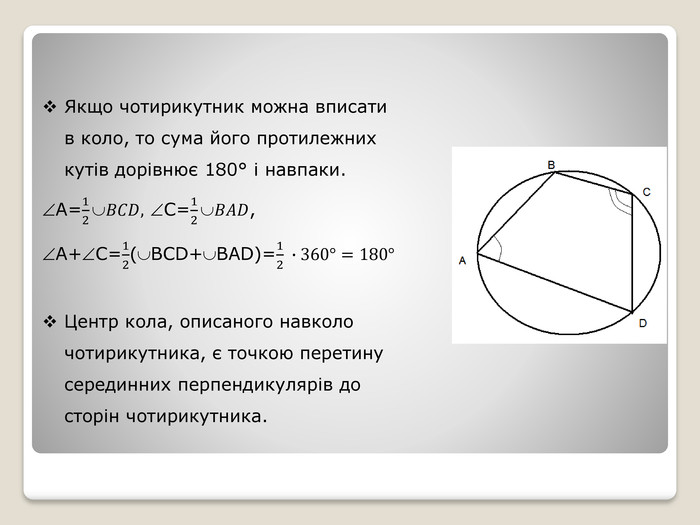
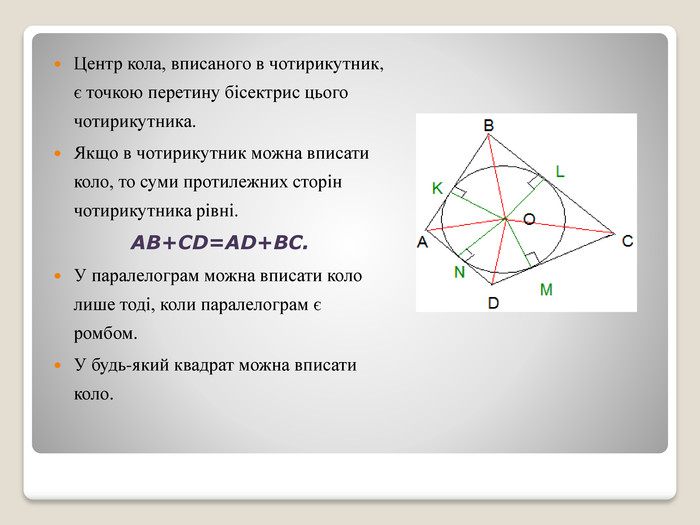
Презентації можна використовувати, як теоретичні відомості по даній темі: «Вписані та центральні кути. Вписані та описані чотирикутники.» В ній міститься означення ба властивості вписаних і центральних кутів, вписаних та описаних чотирикутників.Цей матеріал можуть використовувати вчителі під час підготовки до уроків, а також учні, які самостійно опрацьовують тему.
Вписані та центральні кути Вписані та описані чотирикутники Опришко Олена Василівна, вчитель математики та фізики Деньгівського НВК «ЗОШ І-ІІІ ступенів – дошкільний навчальний заклад»rrrrr
Центральний кут. Кут з вершиною у центрі кола називається центральним кутом. Центральний кут вимірюється відповідною дугою (дугою, на яку він спирається). АОВАОВ = АLВ L
Вписаний кут. Кут,вершина якого лежить на колі,а сторони перетинають коло,називається вписаним кутом. САВLОВписаний кут вимірюється половиною дуги, на яку він спирається, і дорівнює половині відповідного центрального кута.АОВ= 12 АLC
Вписані кути, які спираються на ту саму дугу, рівні між собою. DKCВADKCВAВписаний кут, що спирається на діаметр, дорівнює 90°.ADB = ACB =AKB = 90°ADB = ACB =AKB
Вписані чотирикутники. Чотирикутник, усі вершини якого лежать на колі, називається вписаним у це коло, а коло - описаним навколо даного чотирикутника.
Якщо чотирикутник можна вписати в коло, то сума його протилежних кутів дорівнює 180° і навпаки.А=12𝐵𝐶𝐷, C=12𝐵𝐴𝐷, A+C=12(BCD+BAD)=12 ∙360°=180°Центр кола, описаного навколо чотирикутника, є точкою перетину серединних перпендикулярів до сторін чотирикутника.
Навколо паралелограма можна описати коло, тільки якщо він є прямокутником. Центр такого кола — точка перетину діагоналей прямокутника. Навколо будь-якого квадрата можна описати коло. Навколо трапеції можна описати коло, тільки якщо вона рівнобічна. О
Описані чотирикутники. Чотирикутник називається описаним навколо кола, якщо прямі, що містять сторони чотирикутника, є дотичними до кола.
Центр кола, вписаного в чотирикутник, є точкою перетину бісектрис цього чотирикутника. Якщо в чотирикутник можна вписати коло, то суми протилежних сторін чотирикутника рівні. АВ+СD=AD+ВС. У паралелограм можна вписати коло лише тоді, коли паралелограм є ромбом. У будь-який квадрат можна вписати коло.
Якщо в трапецію вписане коло то :суми бічних сторін дорівнюють сумі основ;висота дорівнює двом радіусам вписаного кола ;бічну сторону видно з центра вписаного кола під прямим кутом.
Використана література: Бурда М.І. Геометрія: Підручник для 8 класу/ Бурда. М.І., Тарасенкова. Н. М. – Київ «Зодіак-ЕКО», 2016.- 240с. Старова О. О. Геометрія 8 клас / Старова О. О. – Харків: Вид.група «Основа», 2016.- 144с. – (Серія «Мій конспект»)rrrrr
про публікацію авторської розробки
Додати розробку