Презентація з алгебри для 10 класу "Тригонометричні нерівності"
Про матеріал
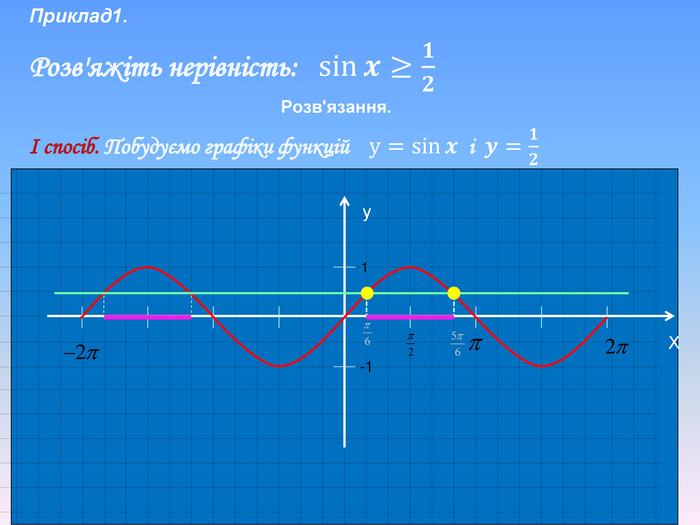
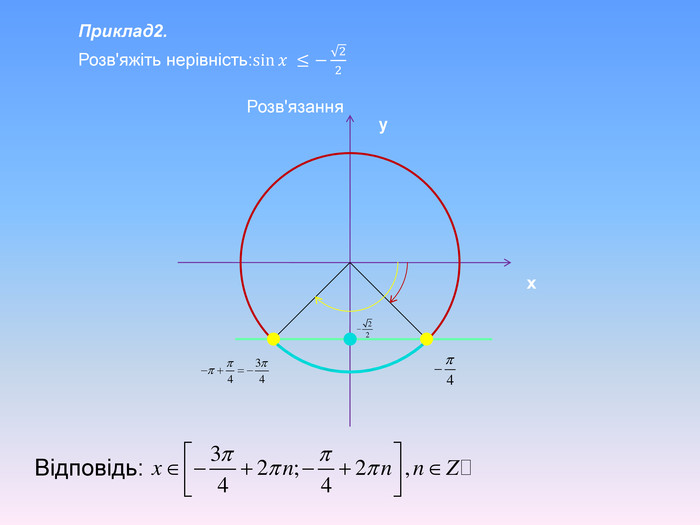
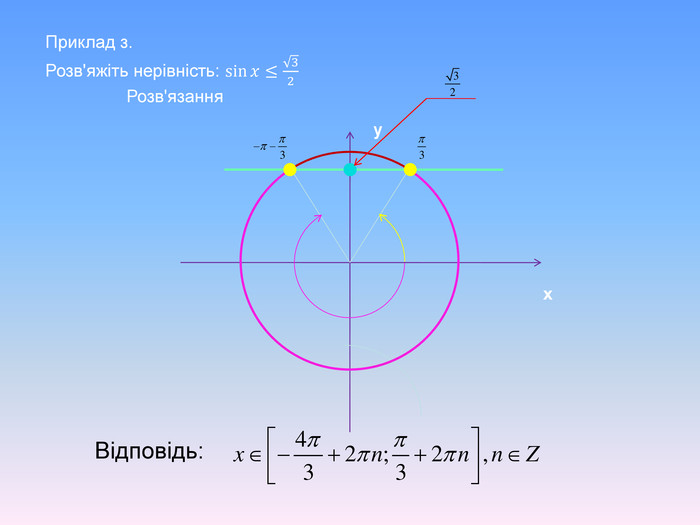
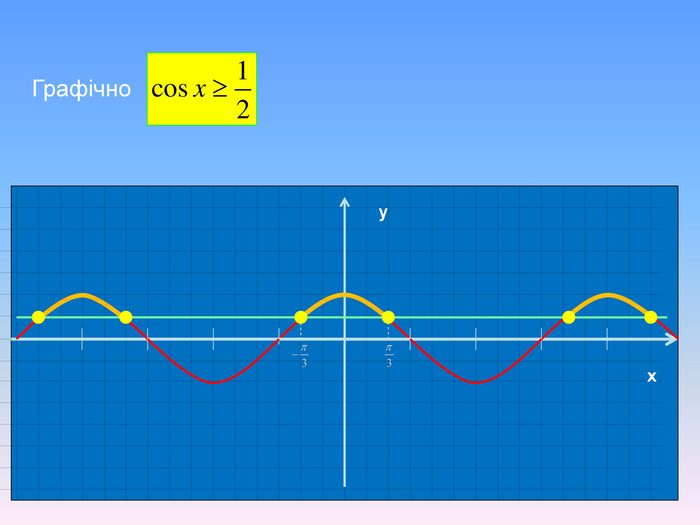
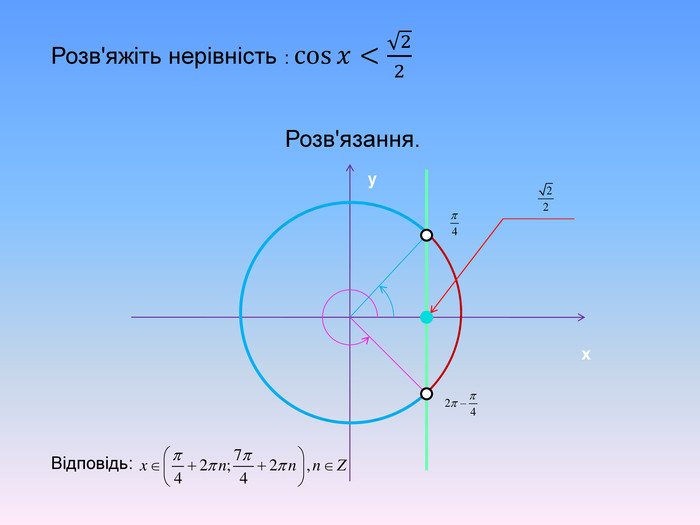
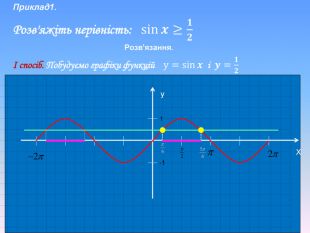
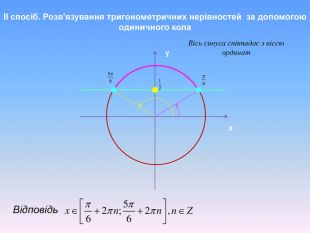
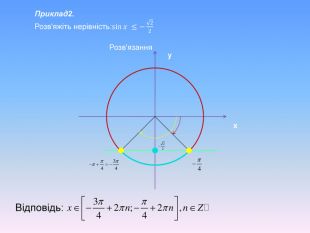
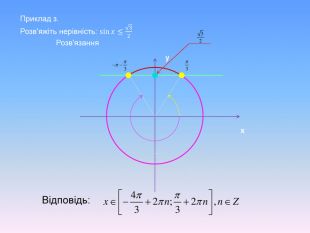
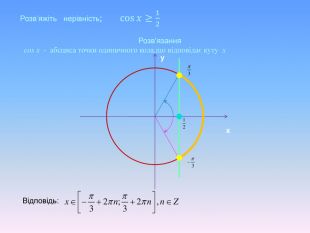
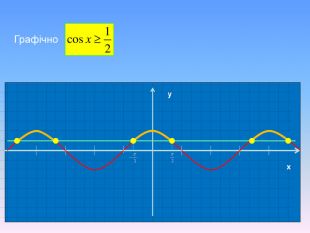
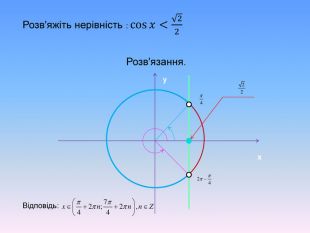
Тригонометричні нерівності розв'язані за допомогою одиничного кола та графічно. Наглядно різними кольорами анімаційнго йде виділення на графіку. Презентація також містить алгоритм розв'язання тригонометричних нерівностей.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку













-

Константинова Олена Павлівна
21.03.2024 в 00:15
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Почуєва Олена Анатоліївна
06.03.2023 в 11:19
Добрий день,колего!
Щиро дякую за розробку та бажання поділитсь.
З повагою,Почуєва О.А.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Котовський Євгеній
13.02.2023 в 09:36
Загальна:
4.7
Структурованість
4.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Свириденко Надія
29.04.2022 в 11:08
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Личко Вікторія Михайлівна
06.12.2021 в 13:05
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Касаткіна Оксана Анатоліївна
09.05.2020 в 17:12
Бажано додати матеріал для розв'язування нерівностей, які містять тангенс і катангенс.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Рязанова Галина Яківна
16.04.2020 в 22:28
Все чудово, але немає розв'язків для нерівностей з тангенсом і котангенсом, але в темі заявлені такі нерівності.
Загальна:
4.3
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
3.0
-

Посохова Людмила Вікторівна
25.02.2018 в 21:25
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Болховецька Наталія Петрівна
22.02.2018 в 10:02
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Туінов Іван Володимирович
21.02.2018 в 19:33
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Туінова Світлана Григоріївна
21.02.2018 в 19:26
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Туінова Тетяна Іванівна
21.02.2018 в 19:15
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 9 відгуків