Презентація з геометрії по темі: "Елементарні геометричні фігури. Трикутники."

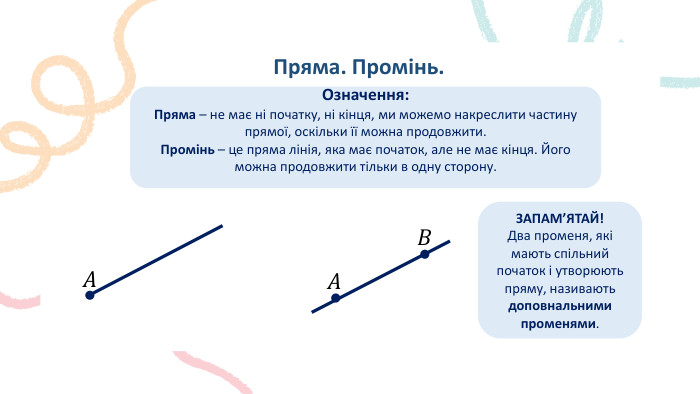
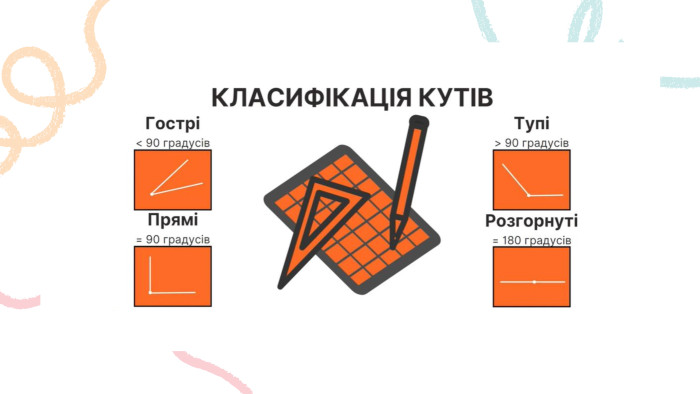
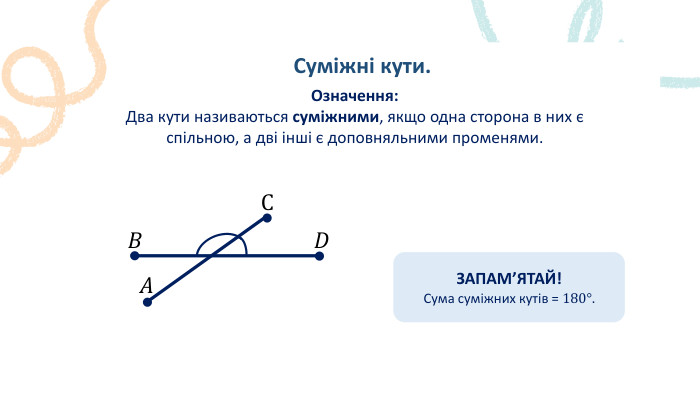
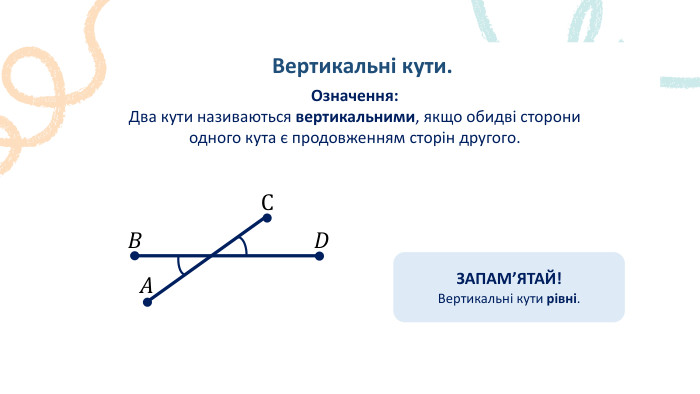
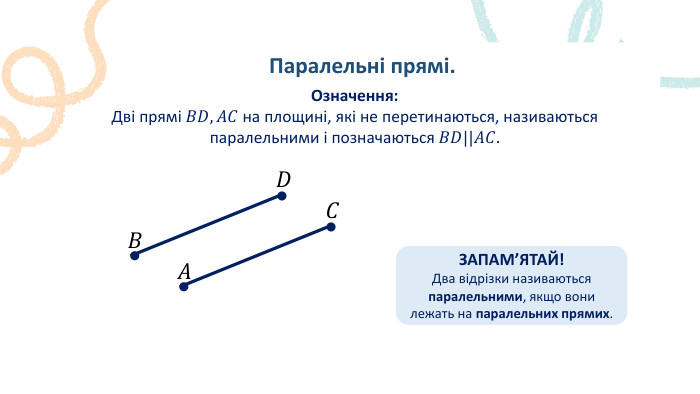
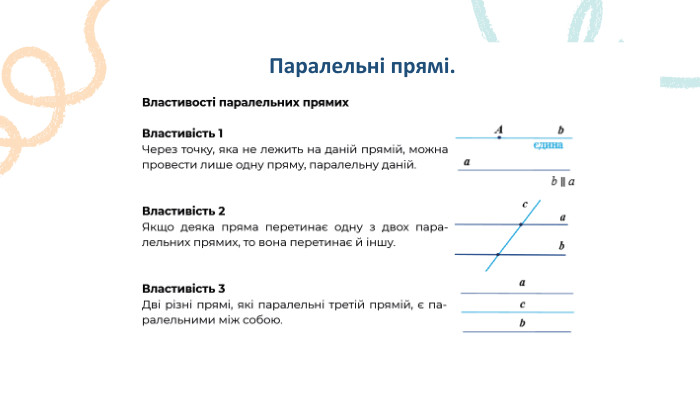
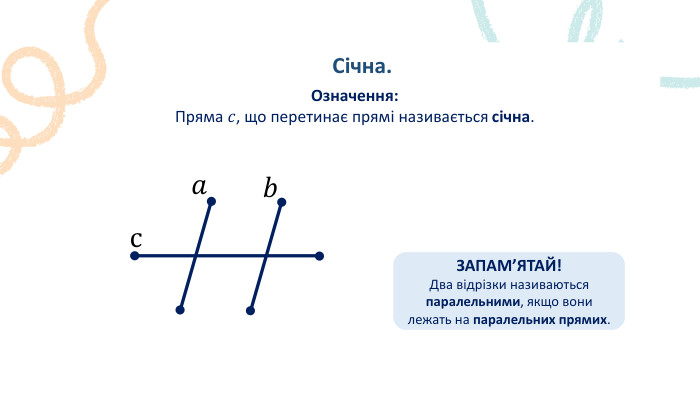
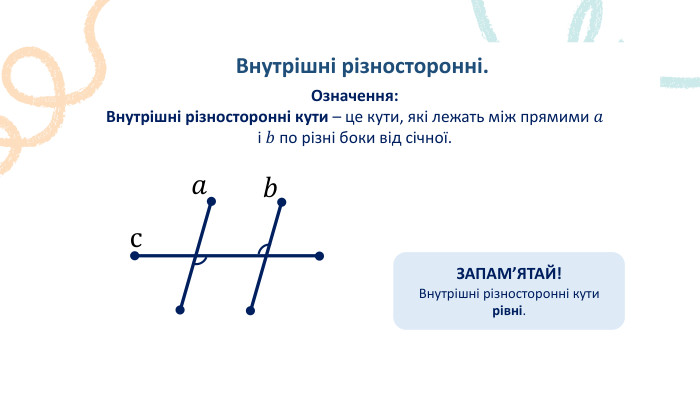
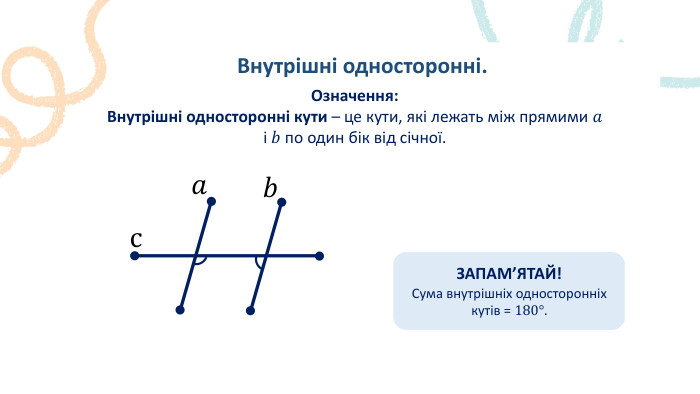
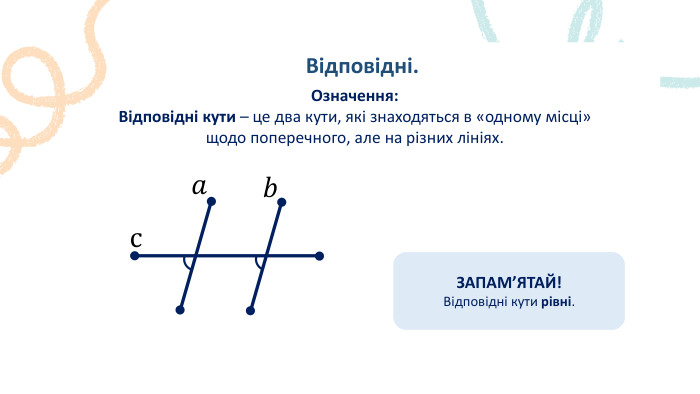
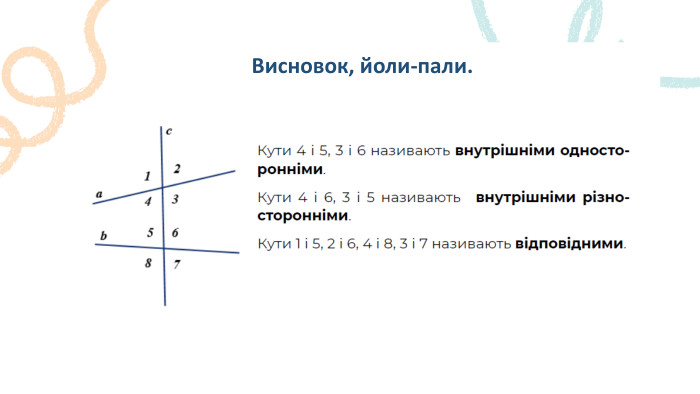
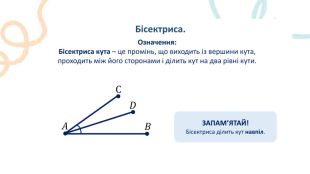
Пряма. Промінь. Означення: Пряма – не має ні початку, ні кінця, ми можемо накреслити частину прямої, оскільки її можна продовжити. Промінь – це пряма лінія, яка має початок, але не має кінця. Його можна продовжити тільки в одну сторону.𝐴 𝐵 𝐴 ЗАПАМ’ЯТАЙ!Два променя, які мають спільний початок і утворюють пряму, називають доповнальними променями.

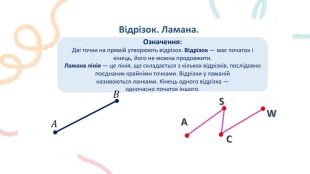
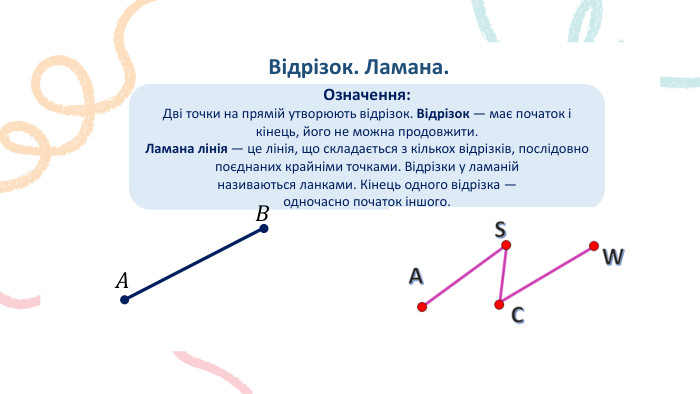
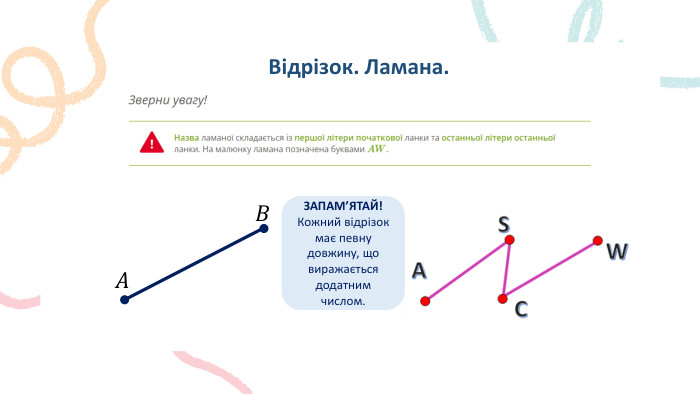
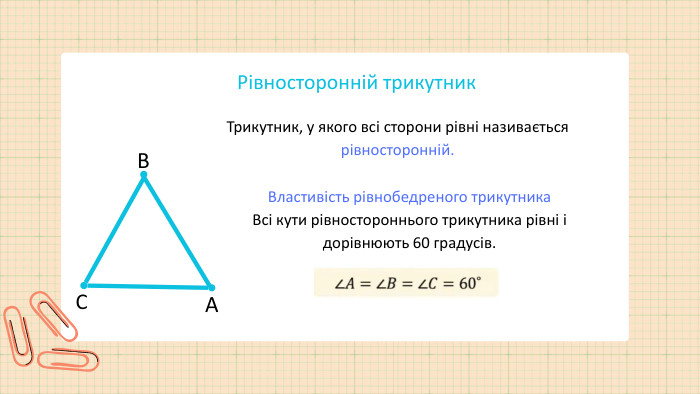
Відрізок. Ламана. Означення: Дві точки на прямій утворюють відрізок. Відрізок — має початок і кінець, його не можна продовжити. Ламана лінія — це лінія, що складається з кількох відрізків, послідовно поєднаних крайніми точками. Відрізки у ламаній називаються ланками. Кінець одного відрізка — одночасно початок іншого.𝐴 𝐵 

Відрізок. Ламана.𝐴 𝐵 ЗАПАМ’ЯТАЙ!Кожний відрізок має певну довжину, що виражається додатним числом.

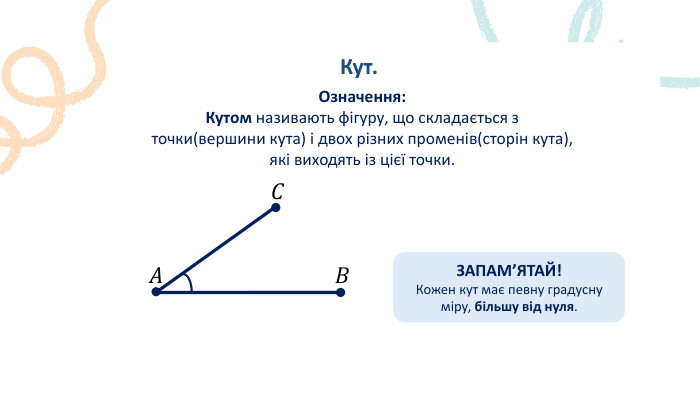
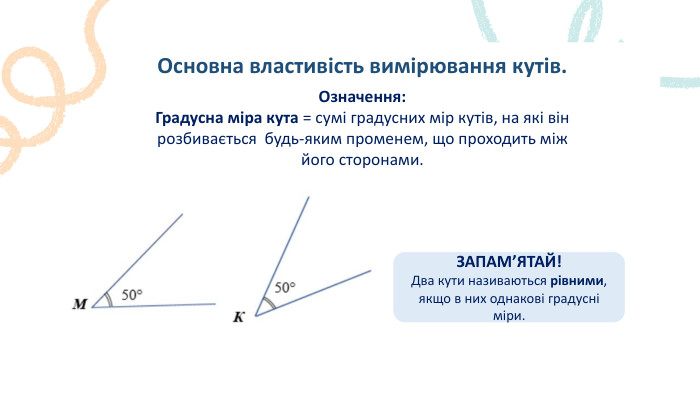
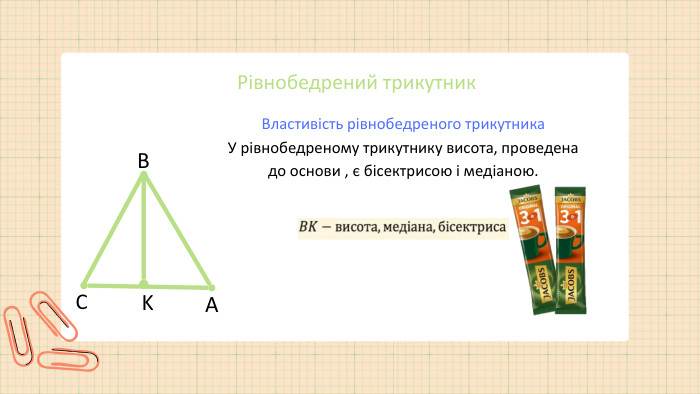
Відрізок. 𝐴 𝐵 𝐶 ЗАПАМ’ЯТАЙ!Довжину відрізка називають відстанню між його кінцями. Розглянемо малюнок. Точка 𝐶 належить відрізку 𝐴𝐵і ділить його на два відрізки: 𝐴𝐶 і 𝐶𝐵. Згідно малюнку. 𝐴𝐶 = 5 см, 𝐶𝐵 = 3 см, 𝐴𝐵= 8 см. Отже, 𝐴𝐶+𝐶𝐵=𝐴𝐵. Цей приклад ілюструє основну властивість вимірювання відрізків: довжина відрізка = сумі довжин частин, на які він розбивається будь-якого його внутрішньою точкою. 

Кут. 𝐴 𝐵 ЗАПАМ’ЯТАЙ!Кожен кут має певну градусну міру, більшу від нуля. Означення: Кутом називають фігуру, що складається з точки(вершини кута) і двох різних променів(сторін кута), які виходять із цієї точки.𝐶 

Основна властивість вимірювання кутів. ЗАПАМ’ЯТАЙ!Два кути називаються рівними, якщо в них однакові градусні міри. Означення: Градусна міра кута = сумі градусних мір кутів, на які він розбивається будь-яким променем, що проходить між його сторонами.

Бісектриса. ЗАПАМ’ЯТАЙ!Бісектриса ділить кут навпіл. Означення: Бісектриса кута – це промінь, що виходить із вершини кута, проходить між його сторонами і ділить кут на два рівні кути.𝐴 𝐵 С 𝐷 

Суміжні кути. ЗАПАМ’ЯТАЙ!Сума суміжних кутів = 180°. Означення: Два кути називаються суміжними, якщо одна сторона в них є спільною, а дві інші є доповняльними променями.𝐴 𝐷 С 𝐵 

Вертикальні кути. ЗАПАМ’ЯТАЙ!Вертикальні кути рівні. Означення: Два кути називаються вертикальними, якщо обидві сторони одного кута є продовженням сторін другого.𝐴 𝐷 С 𝐵 

Паралельні прямі. ЗАПАМ’ЯТАЙ!Два відрізки називаються паралельними, якщо вони лежать на паралельних прямих. Означення: Дві прямі 𝐵𝐷, 𝐴𝐶 на площині, які не перетинаються, називаються паралельними і позначаються 𝐵𝐷||𝐴𝐶. 𝐷 𝐵 𝐴 𝐶 

Паралельні прямі.

Перпендикулярні прямі.

Січна. ЗАПАМ’ЯТАЙ!Два відрізки називаються паралельними, якщо вони лежать на паралельних прямих. Означення: Пряма 𝑐, що перетинає прямі називається січна. с 𝑎 𝑏 

Внутрішні різносторонні. ЗАПАМ’ЯТАЙ!Внутрішні різносторонні кути рівні. Означення: Внутрішні різносторонні кути – це кути, які лежать між прямими 𝑎 і 𝑏 по різні боки від січної. с 𝑎 𝑏 

Внутрішні односторонні. ЗАПАМ’ЯТАЙ!Сума внутрішніх односторонніх кутів = 180°. Означення: Внутрішні односторонні кути – це кути, які лежать між прямими 𝑎 і 𝑏 по один бік від січної. с 𝑎 𝑏 

Відповідні. ЗАПАМ’ЯТАЙ!Відповідні кути рівні. Означення: Відповідні кути – це два кути, які знаходяться в «одному місці» щодо поперечного, але на різних лініях.с 𝑎 𝑏 

Висновок, йоли-пали.

Ознаки паралельності прямих.

Висотою трикутника називають перпендикуляр, проведений із вершини трикутника до протилежної сторони. BH - висота трикутника. Елементи трикутника. ABCH

Висота у тупокутному трикутнику може бути проведена на продовження сторони. BH - висота трикутника. Елементи трикутника. ABCH

Медіаною трикутника називають відрізок, який з’єднує вершину трикутника із серединою протилежної сторони. BH - медіана трикутника. AH=HC. Елементи трикутника. ABCH

Елементи трикутника. BБісектрисою трикутника називається відрізок, який з’єднує вершину кута і точку протилежної сторони і ділить кут навпіл. BK - бісектриса трикутника. ACK

Елементи трикутника. BОсновна властивість бісектриси. ACK

Прямокутний трикутник. Прямокутний трикутник, трикутник у якого один з кутів прямий. Катетами називають сторони, прилеглі до прямого кута. Гіпотенузою називають сторону, протилежну до прямого кута.

Властивості прямокутного трикутника. Сума гострих кутів прямокутного трикутника дорівнює 90 градусів. ABC

Властивості прямокутного трикутника. Якщо у прямокутному трикутнику один із гострих кутів дорівнює 30 градусів, то протилежний цьому катет дорівнює половині гіпотенузи. ABC

BТрикутник називається рівнобедреним, якщо в нього дві сторони рівні. Властивість рівнобедреного трикутника. У рівнобедреному трикутнику кути, прилеглі до основи, є рівними. Рівнобедрений трикутник. AC

BВластивість рівнобедреного трикутника. У рівнобедреному трикутнику висота, проведена до основи , є бісектрисою і медіаною. Рівнобедрений трикутник. AC K

BВластивість рівнобедреного трикутника. Всі кути рівностороннього трикутника рівні і дорівнюють 60 градусів. Рівносторонній трикутник. ACТрикутник, у якого всі сторони рівні називається рівносторонній.