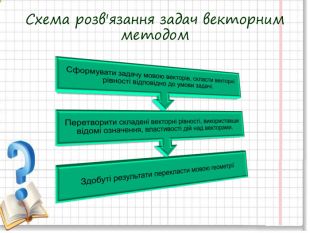
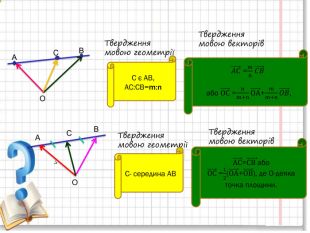
векторний метод розв'язування задач
Про матеріал
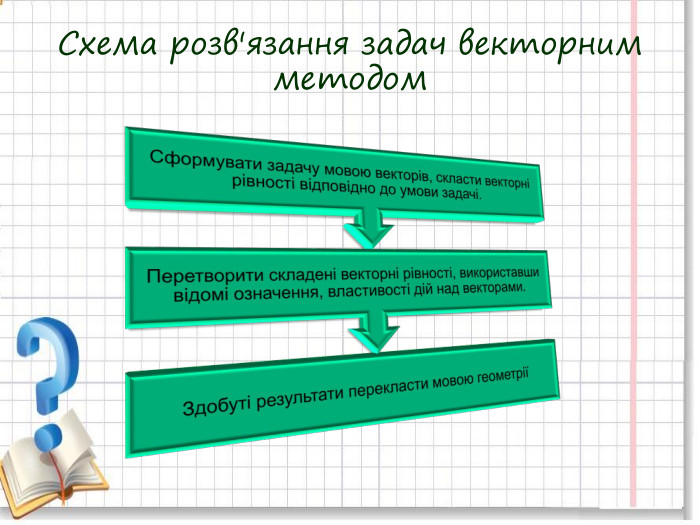
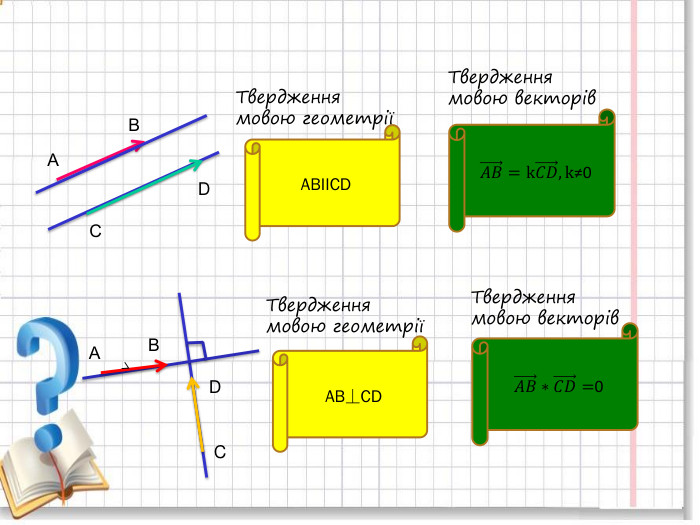
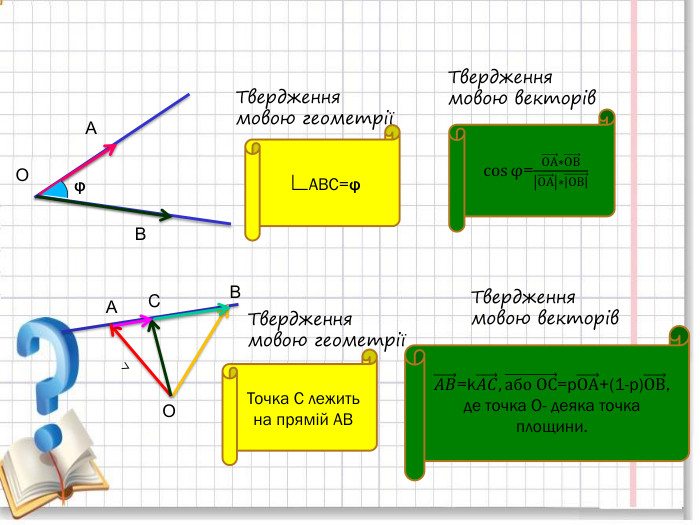
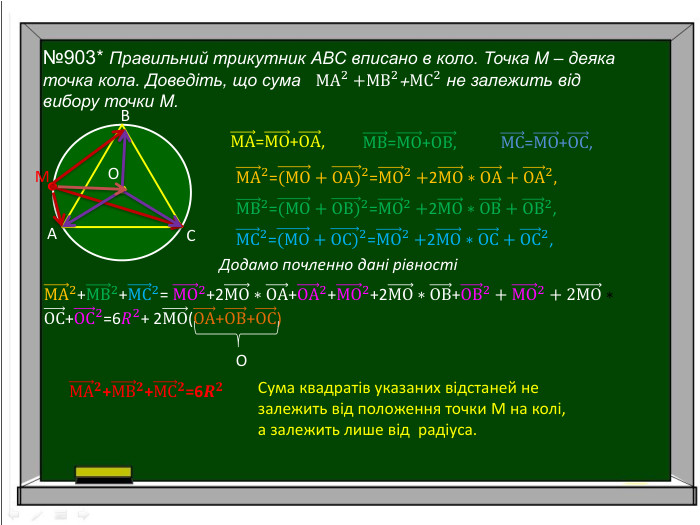
Презентація для уроку геометрії 9 клас з теми "Вектори" підсумковий урок. Підійде для повторення і систематизації знань Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку