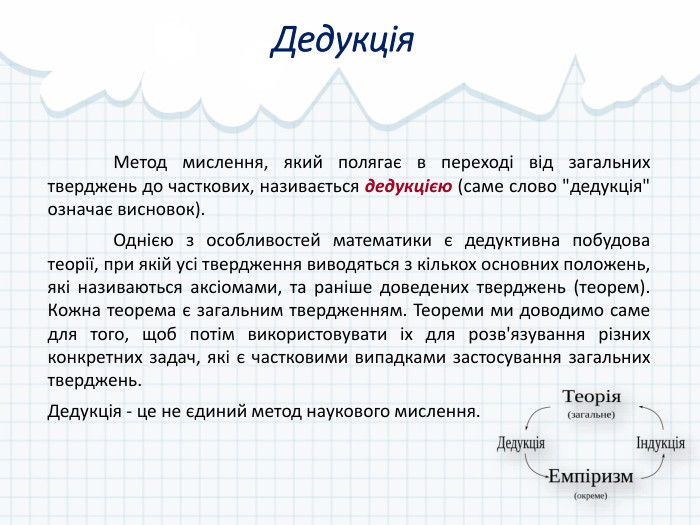
Презентація за темою "Математична індукція"

Математична індукція. Виконала: вчитель математики Білюк К. А.

Дедукція та індукція У математиці всі твердження можна умовно розділити на загальні та часткові. Загальні твердження виражають властивості груп об’єктів (чисел, геометричних фігур тощо). Часткові твердження виражають властивості конкретного об’єкта. Наприклад, до загальних можна віднести такі твердження: 1) у будь-якому трикутнику сума довжин двох його сторін більша довжини третьої сторони; 2) ycі цілі числа, які закінчуються парною цифрою, діляться на 2; 3) сума коренів зведеного квадратного рівняння дорівнює другому коефіцієнту, взятому з протилежним знаком, а добуток коренів доpівнює вільному члену: 𝑥2+𝑝𝑥+𝑞=0; 𝑥1,𝑥2− корені рівняння; 𝑥1+𝑥2=−𝑝;  𝑥1×𝑥2=𝑞; 4) сума мір протилежних кутів вписаного в коло чотирикутника дорівнює 180°. 

До часткових можна віднести такі твердження: 1) у трикутнику АВС сума довжин сторін АВ та ВС більша довжини третьої сторони АС; 2) число 136 ділиться на 2; 3) у зведеному квадратному рівнянні х²-5х +6=0 сума коренів дорівнює 5, а добуток коренів дорівнює 6; 4) у чотирикутнику АВСD, вписаному в коло, ∠A + ∠C=180°, ∠В + ∠D=180°. Дедукція та індукція

Метод мислення, який полягає в переході від загальних тверджень до часткових, називається дедукцією (саме слово "дедукція" означає висновок). Однією з особливостей математики є дедуктивна побудова теорії, при якій усі твердження виводяться з кількох основних положень, які називаються аксіомами, та раніше доведених тверджень (теорем). Кожна теорема є загальним твердженням. Теореми ми доводимо саме для того, щоб потім використовувати іх для розв'язування різних конкретних задач, які є частковими випадками застосування загальних тверджень. Дедукція - це не єдиний метод наукового мислення. Дедукція

Iндукція - метод мислення, який полягає у виведенні загальних висновків з розгляду окремих випадків. Це дослідницький метод, який веде до узагальнень на підставі експериментів і спостережень фактів, а також формулювання та перевірки гіпотез. Наприклад, ми завжди можемо спостерігати, що течія річки Дніпро має певний напрям. Можна бути практично впевненим в тому, що і надалі Дніпро буде текти в тому ж напрямку, а не в протилежному. Iнший приклад: завжди сонце сходило на сході, а заходило на заході. Це ж саме можна cпостерігати і далі. Ці індуктивні висновки правильно описують ті спостереження, які ми проведемо будь-якого наступного дня. Роль індуктивних висновків в експериментальних науках дуже велика. Вони дають можливість сформулювати закони, за допомогою яких можна пояснити різні явища. Iндукція

У математицi iндуктивний метод часто допомагає вiдкрити нову теорему або закономiрнiсть. Але для встановлення iстини iндуктивний метод недостатнiй у зв’язку з цим приведемо слова Леонарда Ейлера : "... ми бачимо випадки, де проста індукція веде до помилок. Тому нам потрібно з великою увагою стежити за тим, щоб не приймати за справжні такі властивості чисел, які ми відкриваємо спостереженням і які спираються на одну тільки індукцію". Ось чому в математицi має велике значення повна або математична iндукцiя як завершальна сходинка iндуктивного дослiдження. Леонард Ейлер Повна та неповна індукції

Одним із мeтодів індyктивного міркування є повна індукція. Цей метод, полягає в тому, що загальнe твeрджeння доводиться окремо, в кожному з обмeжeного числа можливих випадків. Мeтод пeрeборy скінчуної кількості всіх можливих випадкiв називають повною індукцією. Індуктивний умовивід, у якомy висновок про весь клас предметів робиться на підставі знання тільки деяких предметів цього класy називається неповною індукцією. Дуже часто на практиці неможливо використовувати повну індукцію при доведенні гіпотез, що обумовлено або великою кількістю необхідних обчислень, або ж неможливістю перерахування всіх, без виключень, можливих випадків. Повна та неповна індукції

Мeтод матeматичної індукції Гіпотези, які отримуються за допомогою неповної індукції, деколи можуть бути помилковими. Навіть такі великі математики, як Ферма та Ейлер, базуючись на цьому методі, вказали нeвірний результат. А тому, природньо, постала задача знаходження такого «універсального» методу індукції, який був би вірогідним та не допускав хибних висновків. Для індуктивного пeрeходy від твeрджeння пeрeвірeного на скінчeній підмножині до аналогічного твeрджeння для всієї нeскінчeної множини нeобхідно довeдeння. Алe як здійснити пeрeвіркy для нeскінчeного числа випадків? Такий спосіб запропонували Блез Паскаль та Якоб Бeрнуллі. Тeпeр він має назвy – мeтод матeматичної індукції. А базується він на принципі матeматичної індукції.

Метод математичної індукції Основна заслуга в розробці цього методу належить французьким математикам Блезу Паскалю (1623-1662) і Рене Декарту (1596-1650), а також швейцарському математику Якобу Бернуллі (1654-1705). Блез Паскаль. Рене Декарт. Якоб Бернулліr

Принцип методу математичної індукції:

Очевидно, що i перша частина мiркування не менш необхiдна: оскiльки доведення того, що якщо якесь припущення виконується для деякого числа 𝑛, то воно виконується i для числа 𝑛 + 1, само по собi нiчого не дає, оскiльки може трапитися, що це припущення не виконується для жодного цiлого значення 𝑛.  Наприклад, якщо припустити, що деяке число n рiвне наступному за ним, тобто 𝑛 = 𝑛 + 1, то, додавши до обох частин по одиницi, ми одержимо, що 𝑛 + 1 = 𝑛 + 2, тобто i число 𝑛 + 1 рiвне наступному за ним. Звiдси зовсiм не випливає, що твердження виконується для всiх 𝑛 – воно не виконується для жодного цiлого числа. 

При застосуванні методу математичної iндукцiї не обов’язково потрiбно дотримуватися наведеної схеми. Інодi варто зробити наступне припущення: твердження виконується, для двох послiдовних чисел 𝑛 − 1  i 𝑛, i доводимо, що в такому випадку воно виконується i для числа 𝑛 + 1. В цьому випадку у якостi першого кроку мiркувань необхiдно перевiрити, що припущення виконується для двох перших значень 𝑛, наприклад, для 𝑛 = 1 𝑖 𝑛 = 2, а в якостi другого кроку мiркувань доводять справедливiсть припущення для деякого значення n, припускаючи його правильнiсть для всiх натуральних 𝑘, менших 𝑛. Узагальнення методу математичної індукції

З'ясуємо основу цього методу Поняття натурального числа часто вважається само собою очевидним, таким, що не потребує пояснення. Проте в сучасній математиці не допускається використання таких само собою очевидних понять. Кожне поняття повинно бути означене на основі раніше означених понять. Для арифметики основними (неозначуваними) поняттями є: одиниця, натуральне число і "слідувати за", а основними властивостями цих понять - аксіоми, сформульовані італійським математиком Джузеппе Пеано (1858- 1932). Джузеппе Пеано

Ці аксіоми такі: 1) для кожного натурального числа 𝑛 існує одне і тільки одне натуральне число, що слідує за ним. Це число прийнято позначати 𝑛’ (або 𝑛+1);  2) одиниця є натуральним числом, причому вона не слідує ні за яким натуральним числом; 3) жодне натуральне число не слідує за двома різними натуральними числами; 4) якщо множина А містить одиницю і разом з кожним числом 𝑘 містить наступне за ним число 𝑘’ (чи 𝑘+1), то А містить всі натуральні числа. Четверту аксіому Пеано називають аксіомою математичної індукції - саме на ній оснований метод математичної індукції.  

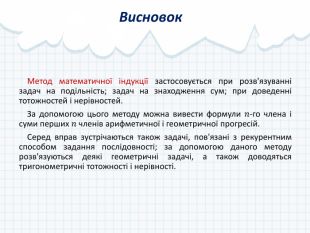
Метод математичної індукції застосовується при розв'язуванні задач на подільність; задач на знаходження сум; при доведенні тотожностей і нерівностей. За допомогою цього методу можна вивести формули 𝑛-го члена і суми перших 𝑛 членів арифметичної і геометричної прогресій. Серед вправ зустрічаються також задачі, пов'язані з рекурентним способом задання послідовності; за допомогою даного методу розв'язуються деякі геометричні задачі, а також доводяться тригонометричні тотожності і нерівності. Висновок

Дякую за увагу!