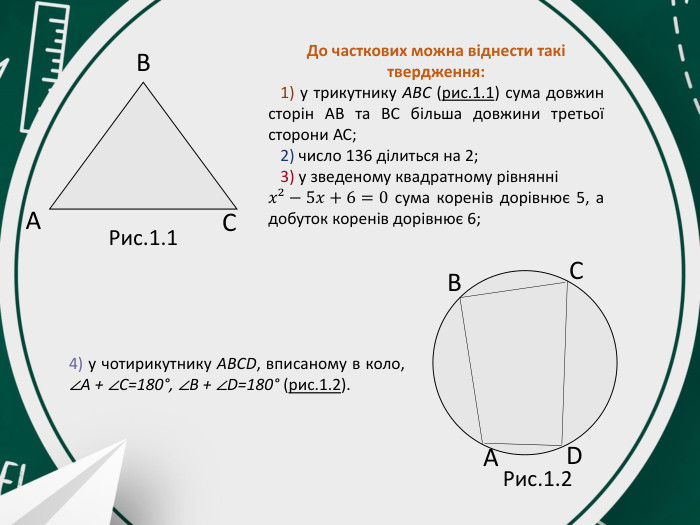
Презентація за темою "Індукція в математиці. Її роль та застосування"

Індукція в математиці. Її роль та застосування. Виконала: вчитель математики Білюк К. А.

Мета Формувати в учнів такі поняття, як індуктивний та дедуктивний методи, повна та неповна індукції; навики застосування методу математичної індукції для розв’язування деяких прикладів. Розвивати логічне мислення, культуру математичного мовлення, вміння готувати повідомлення, вміння вести конспект. Виховувати наполегливість, свідоме ставлення до навчання, пізнавальні інтереси учнів, розширювати кругозір.

Дедукція та індукція У математиці всі твердження можна умовно розділити на загальні та часткові. Загальні твердження виражають властивості груп об’єктів (чисел, геометричних фігур тощо). Часткові твердження виражають властивості конкретного об’єкта. Наприклад, до загальних можна віднести такі твердження: 1) у будь-якому трикутнику сума довжин двох його сторін більша довжини третьої сторони; 2) ycі цілі числа, які закінчуються парною цифрою, діляться на 2; 3) сума коренів зведеного квадратного рівняння дорівнює другому коефіцієнту, взятому з протилежним знаком, а добуток коренів доpівнює вільному члену: 𝑥2+𝑝𝑥+𝑞=0; 𝑥1,𝑥2− корені рівняння; 𝑥1+𝑥2=−𝑝;  𝑥1×𝑥2=𝑞; 4) сума мір протилежних кутів вписаного в коло чотирикутника дорівнює 180°. 

СРис.1.1 АВBACDРис.1.2 До часткових можна віднести такі твердження: 1) у трикутнику АВС (рис.1.1) сума довжин сторін АВ та ВС більша довжини третьої сторони АС; 2) число 136 ділиться на 2; 3) у зведеному квадратному рівнянні𝑥²−5𝑥+6=0 сума коренів дорівнює 5, а добуток коренів дорівнює 6; 4) у чотирикутнику АВСD, вписаному в коло, ∠A + ∠C=180°, ∠В + ∠D=180° (рис.1.2).rr

Дедукція Метод мислення, який полягає в переході від загальних тверджень до часткових, називається дедукцією (саме слово “дедукція” означає висновок). Однією з особливостей математики є дедуктивна побудова теорії, при якій усі твердження виводяться з кількох основних положень, які називаються аксіомами, та раніше доведених тверджень (теорем). Кожна теорема є загальним твердженням. Теореми ми доводимо саме для того, щоб потім використовувати їх для розв’язування різних конкретних задач, які є частковими випадками застосування загальних тверджень. Дедукція – це не єдиний метод наукового мислення.

Індукція Індукція – метод мислення, який полягає у виведенні загальних висновків з розгляду окремих випадків. Це дослідницький метод, який веде до узагальнень на підставі експериментів і спостережень фактів, а також формулювання та перевірки гіпотез. Наприклад, ми завжди можемо спостерігати, що течія річки Дніпро має певний напрям. Можна бути практично впевненим в тому, що і надалі Дніпро буде текти в тому ж напрямку, а не в протилежному. Інший приклад: завжди сонце сходило на сході, а заходило на заході. Це ж саме можна спостерігати і далі. Ці індуктивні висновки правильно описують ті спостереження, які ми проведемо будь-якого наступного дня. Роль індуктивних висновків в експериментальних науках дуже велика. Вони дають можливість сформулювати закони, за допомогою яких можна пояснити різні явища. Теоретична механіка базується на трьох законах Ньютона, а самі ці закони були результатом великої кількості узагальнених дослідних даних.

Індуктивні міркування широко застосовував у своїх дослідженнях з теорії чисел член Петербурзької Академії наук, великий математик XVIII століття Леонард Ейлер. Історія зберегла такий вислів Ейлера:“У мене немає для доведення ніяких інших переконань, за винятком довгої індукції, яку я провів так далеко, що ні в якому разі не можу сумніватися в законі, що керує утворенням цих членів… І здається неможливим, щоб закон, який, як було виявлено, виконується, наприклад, для 20 членів, не можна було б спостерігати і для наступних”. На відміну від дедукції індукція може привести як до правильних, так і до неправильних висновків. Леонард Ейлер(1707-1783)

Наведемо приклади, які спростовують висновок Ейлера. Приклад1. Розглядаючи значення квадратного тричлена 𝑓(𝑛) = 𝑛2 + 𝑛 + 41 при малих натуральних значеннях 𝑛, можна помітити, що ці значення будуть простими числами. Дійсно:  𝑓1= 43; 𝑓2= 47;   𝑓(3) = 53;𝑓(4) = 61. Таким чином, нібито можна зробити висновок, що при будь-якому натуральному n значення виразу 𝑛2 + 𝑛 + 41 є простим числом. Однак, цей висновок неправильний. Якщо 𝑛 = 41, то𝑓(41) = 412 + 41 + 41 = 41· (41 + 1 + 1) = 41· 43. Цей результат є числом складеним. Приклади

Приклад 2. Французький математик XVII століття П’єр Ферма, розглядаючи числа вигляду  22𝑛+1 – прості. При розгляді послідовності перших п’яти чисел виду 22𝑛+1, отримаємо, що числа 221+1=5,  222+1=17,  223+1=257 та  224+1=65537є простими. Проте петербурзький академік Леонард Ейлер довів, що вже при 𝑛=5 число 232+1 ділиться на 641, тобто не є простим. Слід зазначити, що скільки б багато чисел ми б не перевірили, завжди залишається можливість, що серед решти є таке число, для якого дана рівність не буде виконуватися. Тобто, метод неповної індукції дає ймовірні, але не обов’язкові висновки, які можуть виявитись помилковими. Приклади

Приклад 3. Нехай сформульована гіпо-теза: «При будь-якому натуральному значенні 𝑛 число 991𝑛2  + 1 не буде точним квадратом деякого натурального числа». Для заперечення цього твердження довелося перебрати велику кількість чисел, адже перше значення 𝑛 таке, що 991𝑛2  + 1 є точним квадратом деякого натурального числа, має 29 цифр. Приклади

Повна індукція Одним із основних методів індуктивного міркування, як в математиці, так і в прикладних науках, є повна індукція. Нажаль, цей спосіб не часто результативний, що пов’язано з неможливістю доведення конкретних тверджень в кожному окремому випадку.

Неповна індукція Важливу роль при дослідженні має і метод неповної індукції. Базуючись на ньому, часто можна сформулювати правильну гіпо-тезу, яка дозволить розв’язати поставлену задачу. Але, на відміну від повної індукції, яка приводить до істинних висновків, неповна індукція може призвести до хибного висновку.

Висновки В науках, пов’язаних з вивченням природних явищ, часто можна спостерігати повторення деяких закономірностей, на основі яких формулюються загальні висновки та гіпотези. Ці гіпотези, отримані внаслідок окремих випадків, називаються індуктивними, а тому і сам метод цих міркувань – індуктивним методом або індукцією. Метод індукції дозволяє на основі окремих спостережень робити висновки про відповідні загальні закономірності. На відміну від індуктивного методу, який діє від окремого до загального, в математиці та прикладних науках використовують ще й дедуктивний метод: він діє від загального до окремого. Дуже часто обидва цих способи є незамінними при отриманні нових наукових фактів.

Дякую за увагу!