Презентація "Задачі на побудову"
Про матеріал
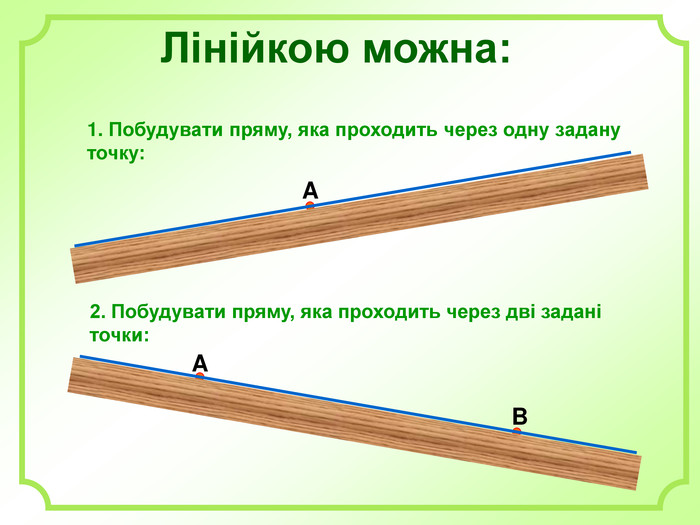
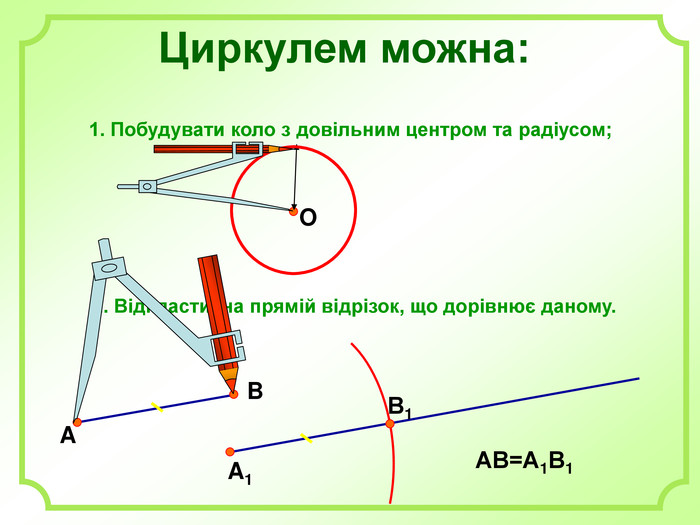
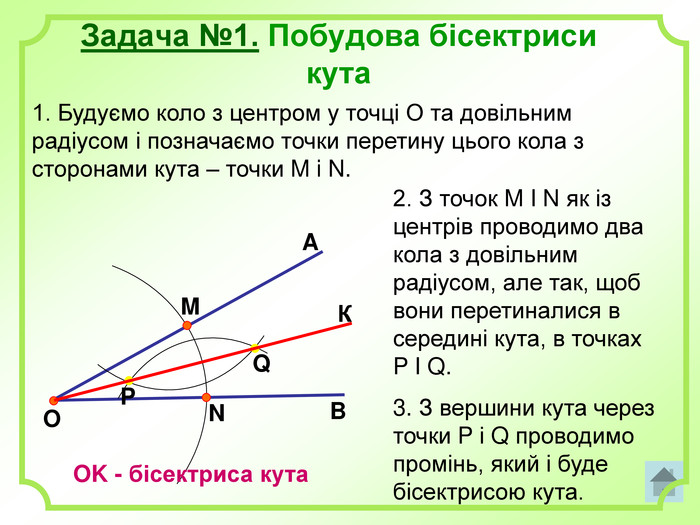
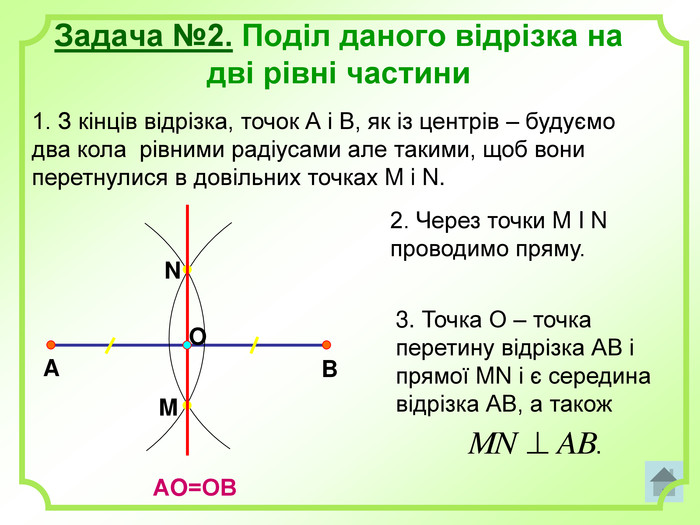
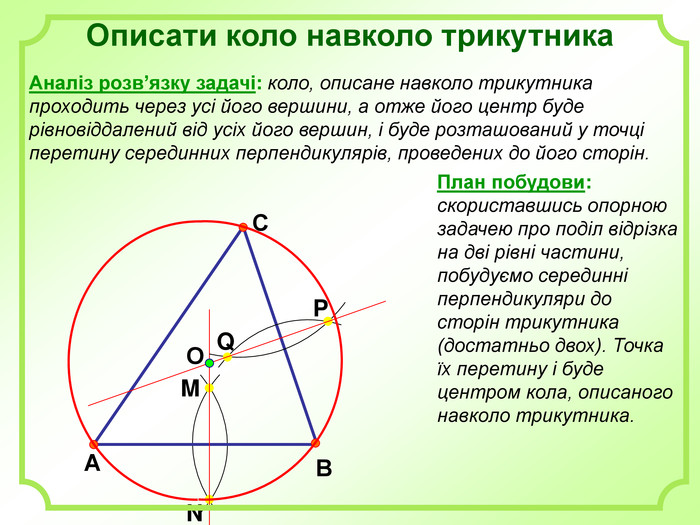
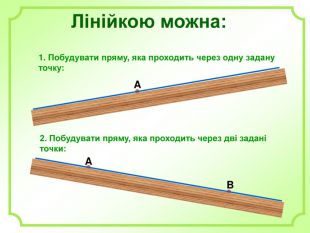
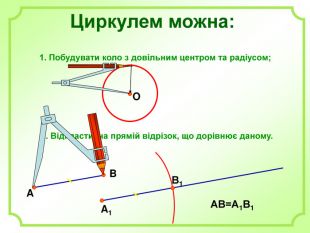
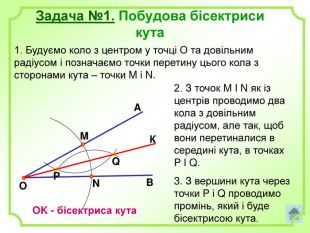
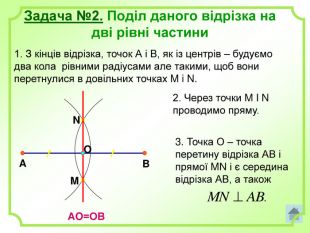
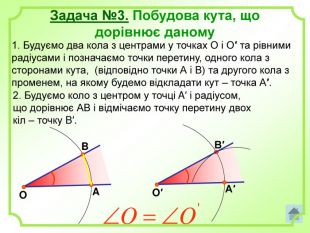
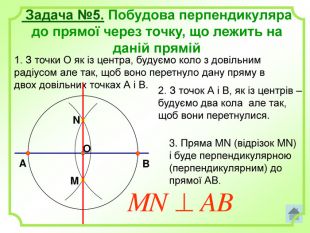
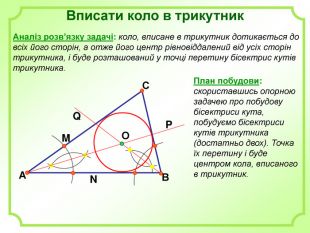
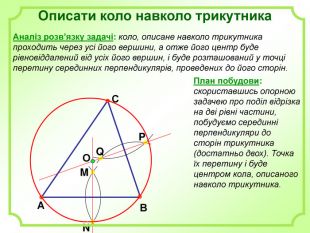
Роз'яснено основні задачі на побудову з використання циркуля і лінійки. А саме: побудова бісектриси кута, побудова серединного перпендикуляра, побудова центрів вписаного і описаного кіл та інші. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку








-

Цмох Василь
13.05.2025 в 15:46
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Вигоднер Діана Ісаківна
11.04.2024 в 13:14
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Колесник Зоя
02.04.2024 в 20:41
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Зелінська Людмила Миколаївна
30.03.2024 в 18:04
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Ляшко Олена
27.02.2024 в 21:15
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Скрипнюк Марія
12.05.2022 в 09:21
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 3 відгука