Презентація "Заміна змінних"

Тема: «Розвязування рівнянь способом заміни змінних»Формування компетентностей:1) Предметна компетентність: повторення і систематизація матеріалу з теми «Рівняння».2)Ключові Компетентності:а) інформаційно – цифрова компетентність – уміти діяти за алгоритмом та складати алгоритм,визначати достатність даних для розв’язання задачі,б) ініціативність і підприємливість – генерувати нові ідеї ,ухвалювати оптимальні рішення,в) соціальна та громадянська компетентності – співпрацювати в команді,виділяти та виконувати власну роль у командній роботі. Тип уроку:удосконалення знань і вмінь.

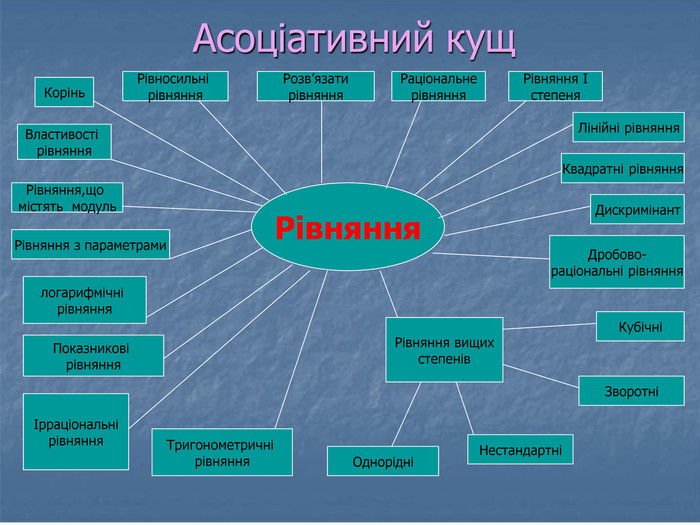
Хід уроку.І. Вступне слово вчителя. Сьогодні на уроці ми здійснимо подорож по країні «Математика», побуваємо в місті «Рівнянь», і від того наскільки ви будете уважними, як правильно виконаєте всі завдання, буде залежати наскільки вдало завершиться наша подорож. Адже рівняння – одне з найважливіших понять математики.ІІ. Актуалізація опорних знань. Складання асоціативного куща « «Рівняння».. 

ІІІ. Удосконалення знань,умінь та навиків. Сьогодні ми з вами продовжимо серію уроків по розв’язуванню рівнянь, які зводяться до квадратних. Ви вже знаєте, що багато рівнянь в математиці за допомогою рівносильних перетворень зводяться саме до квадратних рівнянь. І одним із способів розв’язання таких рівнянь є спосіб заміни змінної. А який тип рівнянь ми будемо розв’язувати використовуючи цей спосіб, ви дізнаєтесь, давши відповіді на запитання математичного кросворда. І. Перша станція нашої подорожі – станція «Інтелектуальна».

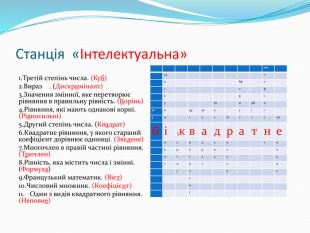
Станція «Інтелектуальна»1. Третій степінь числа.2. Вираз ь² - 4ас.3. Значення змінної,яке перетворює рівняння в правильну рівність.4. Рівняння,які мають однакові корні.5. Другий степінь числа.6. Квадратне рівняння,у якого старший коефіцієнт дорівнює одиниці.7. Многочлен в лівій частині рівняння.8. Рівність,яка містить числа і змінні.9. Французький математик.10. Числовий множник.11. Один з видів квадратного рівняння.

Станція «Інтелектуальна» 1. Третій степінь числа. (Куб) 2. Вираз . (Дискримінант) 3. Значення змінної, яке перетворює рівняння в правильну рівність. (Корінь) 4. Рівняння, які мають однакові корні. (Рівносильні) 5. Другий степінь числа. (Квадрат) 6. Квадратне рівняння, у якого старший коефіцієнт дорівнює одиниці. (Зведене) 7. Многочлен в правій частині рівняння. (Тричлен) 8. Рівність, яка містить числа і змінні. (Формула) 9. Французький математик. (Вієт) 10. Числовий множник. (Коефіцієнт) 11. Один з видів квадратного рівняння. (Неповне) {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}         10к  2д       о  и     8ф е  с     о ф  к     р і  р   6з м9 Вц 1ки 4р5кв уіі ум іве7тлєє11нбі3квадратне нондеи  тп арорнч   о нісаел   в тнит е   н  ьл  н   е   ь          н          і       

Станція «Інтелектуальна» 1. Третій степінь числа. (Куб) 2. Вираз . (Дискримінант) 3. Значення змінної, яке перетворює рівняння в правильну рівність. (Корінь) 4. Рівняння, які мають однакові корні. (Рівносильні) 5. Другий степінь числа. (Квадрат) 6. Квадратне рівняння, у якого старший коефіцієнт дорівнює одиниці. (Зведене) 7. Многочлен в правій частині рівняння. (Тричлен) 8. Рівність, яка містить числа і змінні. (Формула) 9. Французький математик. (Вієт) 10. Числовий множник. (Коефіцієнт) 11. Один з видів квадратного рівняння. (Неповне) {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}         10к  2д       о  и     8ф е  с     о ф  к     р і  р   6з м9 Вц 1ки 4р5кв уіі ум іве7тлєє11нбі3квадратне нондеи  тп арорнч   о нісаел   в тнит е   н  ьл  н   е   ь          н          і       

Третя станція «Біквадратні рівняння»Приклад 1 Розглянемо рівняння 2x4-9x2+4=0– Яке рівняння воно нагадує? 2(х2)2-9x2+4=0. Як розв’язати це рівняння? Воно разв’язується заміною змінної. Нехай х2=t, тоді х4=t2. Маємо рівняння: 2t2-9t+4=0 D= 81-4·4·2=81-32=49t1=(9+7)4=4; t2=(9−7)4=12. Повертаємось до попередньої змінної. Якщо t=4, тоді х2=4. 𝑥1=2𝑥2=−2 Якщо t = 12, тоді х2 = 12. 𝑥3=12 𝑥4=− 12 Відповідь: х = − 12; −2; 12;2 

– Скільки найбільше коренів може мати рівняння такого типу? (4)– Наведіть приклади біквадратних рівнянь і запишіть на дошці. А тепер самостійно розв’яжіть. Приклад 2. x4-10x2+9=0 Відповідь: х = −3;−1;1;3 Приклад 3.x4 - 3x2 - 4=0; Відповідь: -2;2. Учні роблять висновки. Такий спосіб розв’язування рівнянь називають методом заміни змінної. Приклад 4. Розглянемо таке рівняння : (х2-5х)2-4(х2-5х)-12=0– Яким ви способом будете розв’язувати таке рівняння? Нехай х2-5х=а, тоді (х2-5х)2=а2. Одержимо рівняння: а2-4а-12=0; а1=-2; а2=6. Якщо а=-2, то х2-5х=-2 D=17; 𝑥1,2=5±172 Якщо а=6, то х2-5х=6; х2-5х-6=0; х3=6; х4=-1. Відповідь: 5±172; −1;6. Приклад5. Розв’язати рівняння (2х2 + 3х – 1)2 – 10х2 – 15х + 9 = 0(2х2 + 3х – 1)2 – 5(2х2 + 3х – 1) + 4 = 0 Нехай 2х2 + 3х – 1 = t. Тоді t2 – 5t + 4 = 0. Відповідь: -2; 12; −52; 1. 

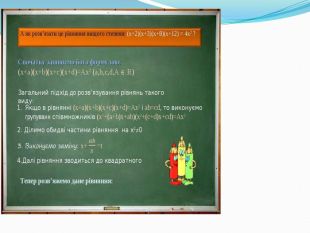
Приклад 6. Розв’язати рівняння : x4 – 8x3 + 15x2 + 4x – 2 = 0. Чи можна розв'язати рівняння методом розкладання на множники, використовуючи схему Горнера? Чому? Виділимо в лівій частині рівняння квадрат двочлена:x4 – 8x3 + 16x2 – х2 + 4x – 2 = 0;(х2 – 4x)2 – (х2 – 4x) – 2 = 0. Зробивши заміну х2 – 4х = t, отримуємо рівняння t2 – t – 2 =0. 𝑡=2𝑡=−1;Звідси 𝑥2−4𝑥=2,𝑥2−4𝑥=−1. Відповідь: 2+6; 2–6; 2+3; 2–3. Приклад7. (х+1)(х+3)(х+5)(х+7)=9. Розкривши дужки, звівши подібні доданки, розкладемо на множники, використавши один із методів, знайдемо корені рівняння. Цей процес тривалий і не раціональний. При розв’язанні таких рівнянь потрібно знайти «вигідний» спосіб групування множників: ((х+1)(х+7))((х+3)(х+5))=9(х2+8х+7)( х2+8х+15)=9 Нехай х2 + 8х = а; (а+7)(а+15) = 9; а2 +22а + 96 = 0. D=484-4·96·1=484-384=100; а1=−22+102=−122=−6; а1=−22−102=−322=−16;Отримаємо два рівняння: х2 + 8х = -6 або х2 + 8х = - 16х2 + 8х + 6 = 0 х2 + 8х +16 = 0𝑥1,2=−8±2102= –4±10 (х+4)2 = 0 х3,4 = ± 4 Відповідь: –4±10; 4; -4. 

Станція «Історична»В проблему розв’язання рівнянь 3-го і 4-го степеня великий вклад зробили італійські математики 16 століття Ніколо. Тарталья, Антоніо Фіоре, Джероламо Кардано та ін. Наприкінці 1534 року Тарталья одержав виклик на математичний турнір від Антоніо Фіоре — учня відомого професора математики Болонського університету Сципіона дель Ферро. Нікколо дізнався, що Фіоре володіє секретом розв'язання багатьох рівнянь, який йому повідомив Ферро. Шляхом титанічних зусиль Тартальї за кілька днів до диспуту теж вдалося знайти спосіб розв'язання такого рівняння. Двобій відбувся 12 лютого 1535 року. Кожному із супротивників треба було розв'язати по 30 задач. За дві години Тарталья впорався з усіма задачами, запропонованими йому Фіоре, а той не розв'язав жодної задачі свого противника. Перемога була повною, вчений прославився на всю Італію і отримав кафедру математики у Вероні. Своїм методом розв'язування рівняння Тарталья поділився з відомим ученим Джироламо Кардано, що був одночасно математиком і механіком, лікарем і алхіміком, хіромантом і особистим астрологом римського папи, взявши з того слово ніколи не публікувати повідомлений йому метод розв'язання. Але через шість років Кардано порушив свою клятву — він видав трактат «Велике мистецтво, або про правила 0алгебри» (1545), де виклав алгоритми розв'язування рівнянь третього і четвертого степеня.

Підсумок уроку.