Різнорівневі завдання з алгебри для учнів 11-х класів за темою: "Показникові рівняння"
Показникові рівняння
|
Методи розв’язання показникових рівнянь: |
Розв’яжи за зразком: |
|
1) Зведення степенів до однакової основи:
а)
Розв’язання: х2 –х = 2; х2 – х – 2 = 0; х1 = 2; х2 = -1. Відповідь: -1; 2
б) 2х
Розв’язання: Так як 5х+2 = 5х
10х 10х = 100; 10х = 102; х =2. Відповідь: 2 |
|
|
2) Винесення спільного множника за дужки: 2х-1 + 2х+2 = 36.
Розв’язання: Так як 2х+2 = 2х-1 2х-1 ( 1 + 23 ) = 36;
2х-1 2х-1 = 4; 2х-1 =22; х-1 = 2; х = 3. Відповідь: 3. |
5х – 5х-2 = 600. |
|
3) Введення нової змінної: 4х + 2х+1 – 24 = 0. Розв’язання:
Так як 4х = (22)х = (2х)2 = і 2х+1 =2х
(2х)2 + 2х Замінемо 2х = а, тоді маємо рівняння: а2 + 2а – 24 = 0; а1 = 4; а2 = -6. Повертаючись до заміни, маємо: 2х = 4; або 2х = -6; х = 2, немає коренів Відповідь: 2. |
25х + 10 |
|
4) Зведення до однорідного рівняння:
6
Розв’язання: Так як 6х = 3х
6 Розділимо обидві частини рівняння на 22х :
Замінемо
а1 = Повертаючись до заміни, маємо:
х1 = 1; х2 = -1. Відповідь: -1; 1.
|
4х + 10х = 2 |
Варіанти різнорівневих завдань для учнів 11-х класів з теми: «Показникові рівняння»
|
(9 б) В - 1 |
(9 б) В - 2 |
|
Розв’яжіть рівняння:
а) 64*
б) 4х + 2*2х -80 =0;
в) 2х – 2х - 4 = 15;
г)
д)
|
Розв’яжіть рівняння:
а) б) 72х - 6*7х + 5 =0;
в) 2х+3 – 2х = 112;
г)30,5(х – 5) = 3
д) |
|
(12б) В - 3 |
(12б) В - 4 |
|
Розв’яжіть рівняння:
а)
б) 6х + 6х+1 = 2х + 2х+1 + 2 х+2 ;
в) 101+х – 101-х = 99 ;
г) 62х+4 = 2х+8
|
Розв’яжіть рівняння:
а)
б) 3х-1 + 3х + 3х+1 = 12х-1 + 12х ;
в) 51+х – 51-х = 24 ;
г) 203х+2 = 4х+12
|


про публікацію авторської розробки
Додати розробку

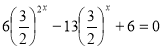 ;
;
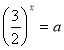 , тоді а
, тоді а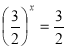 або
або 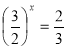 ;
;
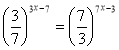 ;
;
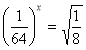 ;
;