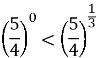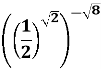Тема: Показникова функція, її графік і властивості.

11 клас алгебра

 ^{[ дата ]}

Тема:  Показникова функція,  її  графік і властивості.

Мета:

• Навчальна: засвоїти означення показникової функції, властивості показникової функції, навчитися будувати графіки показникової функції; засвоїти властивості степенів з дійсним показником на основі властивості степенів з раціональним показником;

• Розвиваюча: розвивати вміння аналізувати графіки показникової функції та користуючись побудованими графіками аналізувати властивості показникової функції;
• Виховна: виховувати інтерес до вивчення точних наук, показати, де саме застосовують у житті властивості показникової функції;

Компетенції:

• Спілкування державною мовою (уміння ставити запитання і розпізнавати проблему; міркувати, робити висновки на основі інформації, поданої в науковій презентації)

Тип уроку: засвоєння нових знань;

Обладнання: опорний конспект, навчальна презентація, мультимедійне обладнання, презентер;

Хід уроку

1. Організаційний етап

• Привітання
• Перевірка присутніх на уроці
• Налаштування на роботу

2. Актуалізація опорних знань

3. Вивчення нового матеріалу

• Показникова функція

Функція виду називається показниковою.

Наприклад:

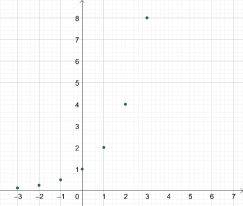
Побудуємо для деяких цілих значень.

Тепер на цьому ж графіку добудуємо деякі дробові значення функції

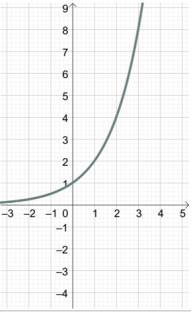
Якщо побудуємо всі значення з множини , то отримаємо графік показникової функції (можливий інший запис, наприклад: ).

*Кожна точка цього графіка є степенем числа 2 з дійсним показником .

• Чи існує функція при

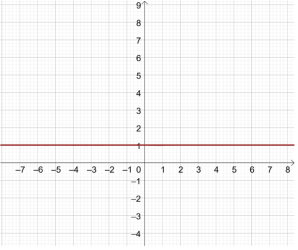
• Існує, але це вже буде не показникова функція. Графіком такої функції є пряма.

• Чи може отриманий графік показникової функції перетнути вісь абсцис?

• Ні, навіть якщо ми візьмемо від’ємний показник степеня, то завжди отримаємо додатне значення

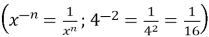
Отже, вісь є асимптотою цього графіка.

*Асимпто́такриво́ї (грец. ασυμπτωτος — що не збігається, не дотикається) — це пряма, до якої крива при віддаленні в нескінченність наближається як завгодно близько.

Проаналізуємо графіки показникової функції при і :

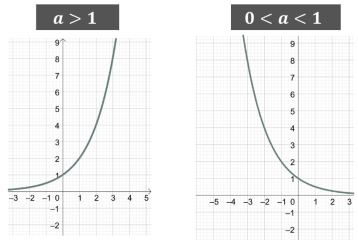
• Що можемо сказати про ці функції на перший погляд?

(при функція зростаюча, при функція спадна)

Побудуємо деякі графіки функцій при і

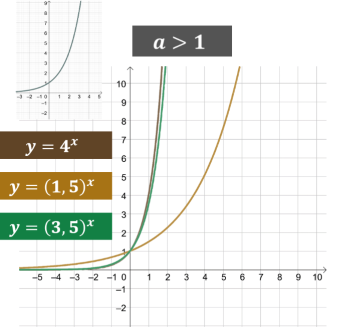
Чим більшою є основа , тим крутіше «піднімається» графік функції , якщо рухатися вправо.

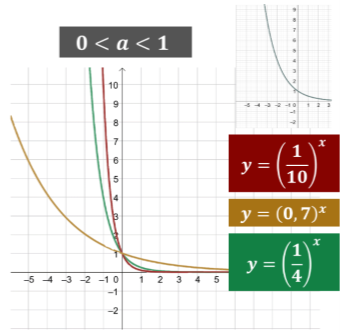
Чим меншою є основа, тим крутіше «піднімається» графік функції , якщо точка рухається вліво.

• Пригадаємо властивості степеня з раціональним показником.

Всі ці властивості справедливі для а та будь-яких дійсних

• Властивості показникової функції

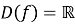1. (Областю визначення показникової функції є множина дійсних чисел)

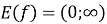2. (Областю значень показникової функції є множина )

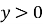3. при всіх значеннях 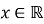(Показникова функція немає нулів, і проміжок 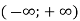є проміжком її знакосталості)

4. При 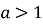зростаюча (При 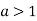зростає на всій області визначення)

При спадна(При спадає на всій області визначення)

• Цікаво

Розглянемо графіки показникових функцій .

У них кутовий коефіцієнт дотичної проведеної в точці до графіка менший за одиницю або більший за одиницю.

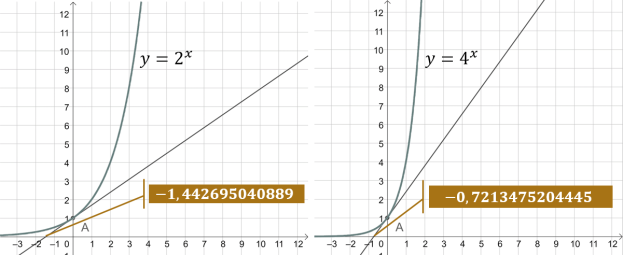
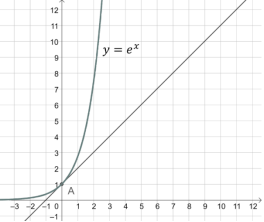
• Чи існує така показникова функція, щоб кутовий коефіцієнт дотичної до її графіка в т. 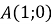дорівнював 1?

Якщо за основу показникової функції взяти ірраціональне число 

Така показникова функція називається експонентою.

• Чому графік кожної показникової функції обов’язково проходить через точку ?

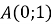• Процеси, що описує показникова функція

Показникова функція описує значну кількість процесів, що відбуваються в природі. Наприклад, зростання кількості бактерій за сприятливих для них умов існування можна описати за законом ().

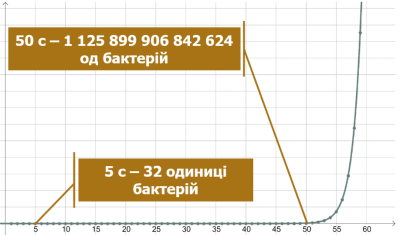
• Як людина використовує ріст і розмноження бактерій?

(Виробництво антибіотиків, кисломолочних продуктів, виноробство, медицина)

• Зростання кількості деревини можна порахувати за законом ()

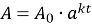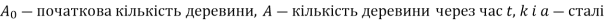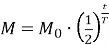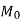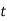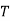• Зменшення маси речовини під час радіоактивного розпаду відбувається за законом ( – початкова маса речовини, – маса в момент часу , – період напіврозпаду речовини (час розпаду половини атомів заданої речовини))

• Зменшення тиску повітря з висотоювідбувається за законом 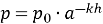( 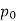– тиск на рівні моря, 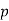– тиск на висоті 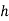, 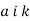- сталі)

4. Закріплення нових знань та вмінь учнів

№1

Яка з даних функцій є показниковою:

№2

Ґрунтуючись на які властивості показникової функції можна стверджувати, що:

Відповідь: При показникова функція є зростаючою, при – спадною.

№3

Побудуйте графік функції . У яких межах змінюється значення функції, коли зростає від до включно?

Розв’язок:

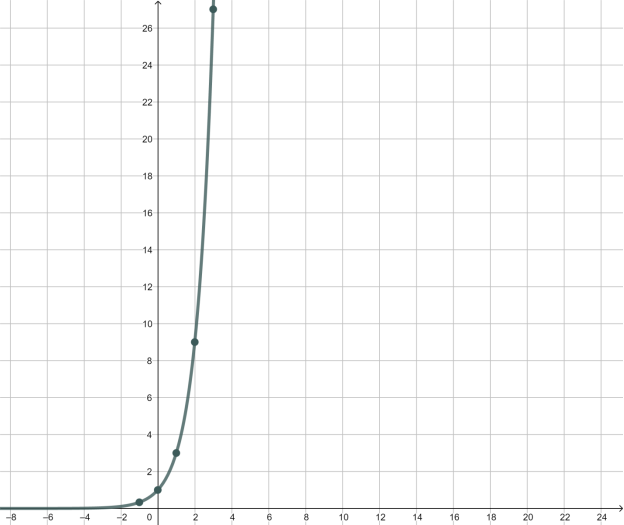
Відповідь: значення функції змінюється від до .

№4

Порівняйте:

№5

Обчисліть значення виразу:

Розв’язок:

Розв’язок:

Розв’язок:

Розв’язок:

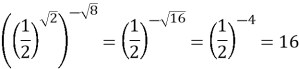
№6

Чи є правильним твердження:

1. Найбільше значення функції 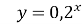на проміжку 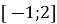дорівнює 5;

Розв’язок:

– спадна

На проміжку її найбільшим значенням буде , отже твердження правильне.

2. Областю визначення функції 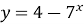є множина дійсних чисел;

Розв’язок:

Твердження правильне, за означенням показникової функції.

3. Областю значень функції 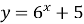є проміжок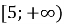

Розв’язок:

Твердження не правильне.

4. Найменше значення функції 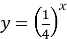на проміжку 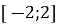дорівнює 16

Розв’язок:

Твердження не правильне.

№7

На якому проміжку найбільше значення функції дорівнює 16, а найменше дорівює

Розв’язок:

Відповідь:

№8

Графік якої з функцій, зображених на рисунках, перетинає графік функції більше ніж в одній точці?

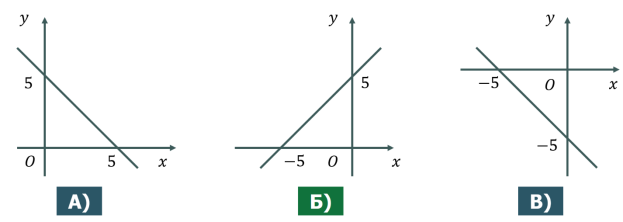
5. Підсумок уроку

• Яку функцію називають показниковою?
• Чи може показникова функція перетнути вісь абсцис?
• Які властивості має степінь з дійсним показником?
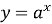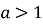• Зобразіть схематично графік функції при ; при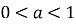
• Через яку точку проходять всі графіки всіх показникових функцій?
• Користуючись побудованими графіками показникових функцій, охарактеризуйте всі їх властивості
• Що називають експонентою?
• Яку цікаву особливість має експонента?
• За якої умови показникова функція зростає? А за якої – спадає?
• Чи може значення показникової функції бути від’ємним?
• Чи може значення показникової функції дорівнювати нулю?

6. Домашнє завдання