Застосування теорії графів до розв’язання задач

В математичній теорії графів та інформатиці граф – це множина точок (вершин), які з’єднані між собою лініями, що називаються дугами або ребрами.

Об’єкти розглядаються як вершини або вузли графу, а зв’язки – як дуги або ребра. Для різних областей використання видів графів можуть відрізнятися орієнтовністю, обмеженнями на кількість зв’язків і додатковими даними про вершини або ребра.

Велика кількість структур, які мають практичну цінність в математиці та інформатиці, можуть  бути представлені графами. Наприклад , будову Вікіпендії можна змоделювати за допомогою орієнтованого графу, в якого вершини – це статті, а дуги (орієнтовані ребра) – посилання на інші статті.

Перша робота про графи з'явилася в 1736 році в публікаціях Петербурзької академії наук. Вона належить Леонарду Ейлера і пов'язана з вирішенням задачі про Кенігсбергскі мости. Мости через річку Прегель розташовані як на малюнку. Питання полягає в тому, чи можна, прогулюючись по місту, пройти через кожен міст точно по одному разу і повернутися назад.

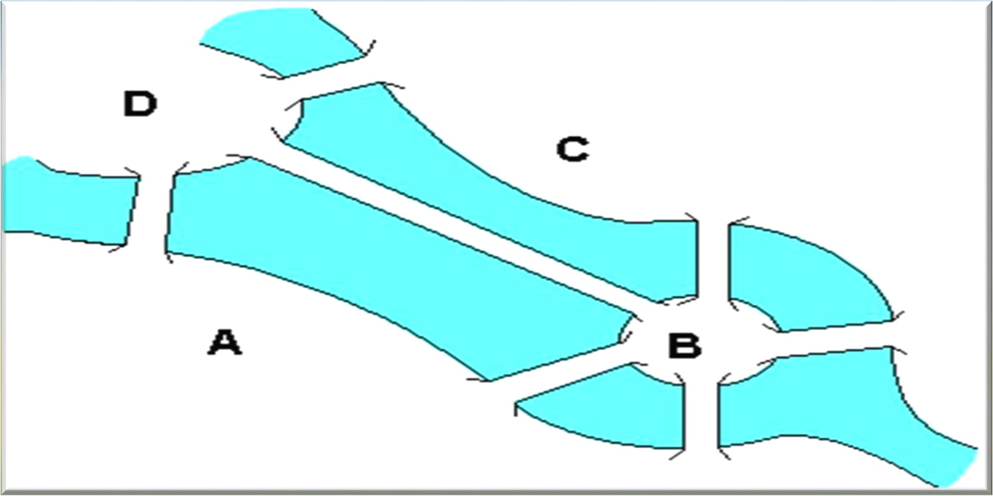
Цю задачу можна представити у вигляді геометричної схеми, на якій точки зображують частини суші, а лінії, їх з'єднують - мости.

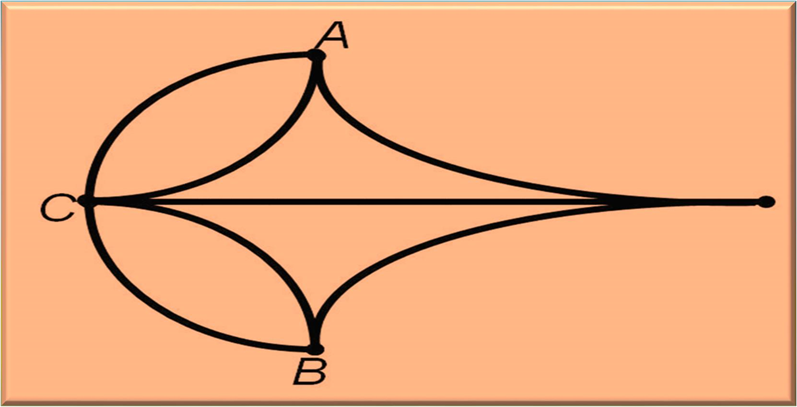
З теорією графів пов'язані також завдання на креслення фігури одним розчерком. Якщо степінь всіх вершин парні, то можна обійти всі вершини графа без повторень, також можна обійти всі вершини, якщо на графі тільки 2 непарні вершини, якщо ж непарних вершин більше, то обійти всі вершини графа не вдасться. У перекладі на мову задачі "одним розчерком" це звучить так: "Якщо на малюнку всі точки парні, то такий малюнок можна намалювати однією лінією, не відриваючи олівця від паперу і не проводячи двічі по одній лінії; якщо на малюнку 2 непарні точки (якщо є одна непарна точка, то обов'язково є і друга), то такий малюнок також можна намалювати одним розчерком, причому слід починати з однієї непарній точки і закінчувати в інший непарній точці; якщо ж непарних точок більше двох, то намалювати такий малюнок одним розчерком не вдасться . "

На малюнку зображена решітка. Чи можна провести безперервну лінію, що перетинає точно по разу кожну сторону грат?

Так обвести однією лінією малюнок не можна, тому він містить відразу 8 непарних точок.

На малюнку зображена пташка. Чи можна намалювати її не відриваючи руки, тобто  чи можна намалювати одним розчерком.

Види графів:

Неорієнтовані графи

Задача 1

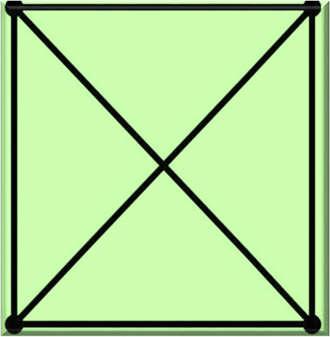
У шаховому турнірі брали участь 4 людини. Кожен спортсмен зіграв зі всіма іншими учасниками змагань по одному разу. Скільки всього було зіграно партій?

                                                                                                                                    1                                                                               2           Для того щоб

Зобразимо відповісти на учасників запитання задачі,

треба лише турніру підрахувати число

точками, а зіграні

ними партії -проведених

відрізків, їх 6.

відрізками.                                   ₄3                                                                        Отже, було зіграно

6 партій.

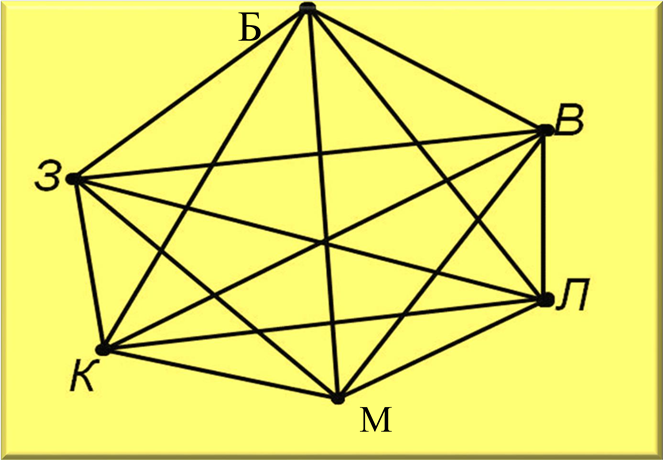Задача 2. На лісовій галявині зустрілися заєць, білка, лисиця, вовк, ведмідь і куниця. Кожен, вітаючись, потиснув кожному лапу. Скільки всього лапопотискань було зроблено?

Задача 3

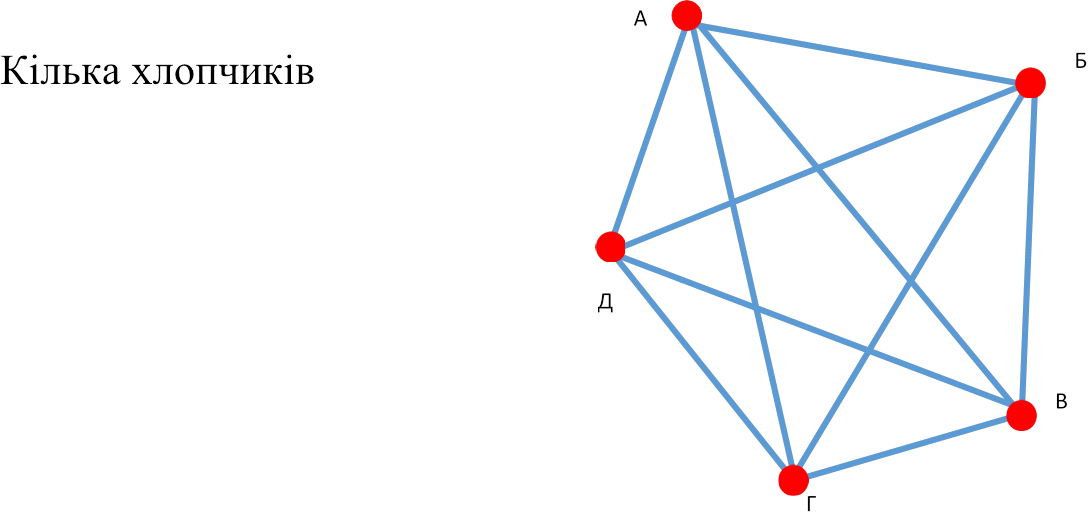зустрілися на вокзалі, щоб поїхати за місто в ліс. При зустрічі всі вони привіталися один з одним за руку. Скільки хлопчиків поїхало за місто, якщо всього було10 рукостискань?

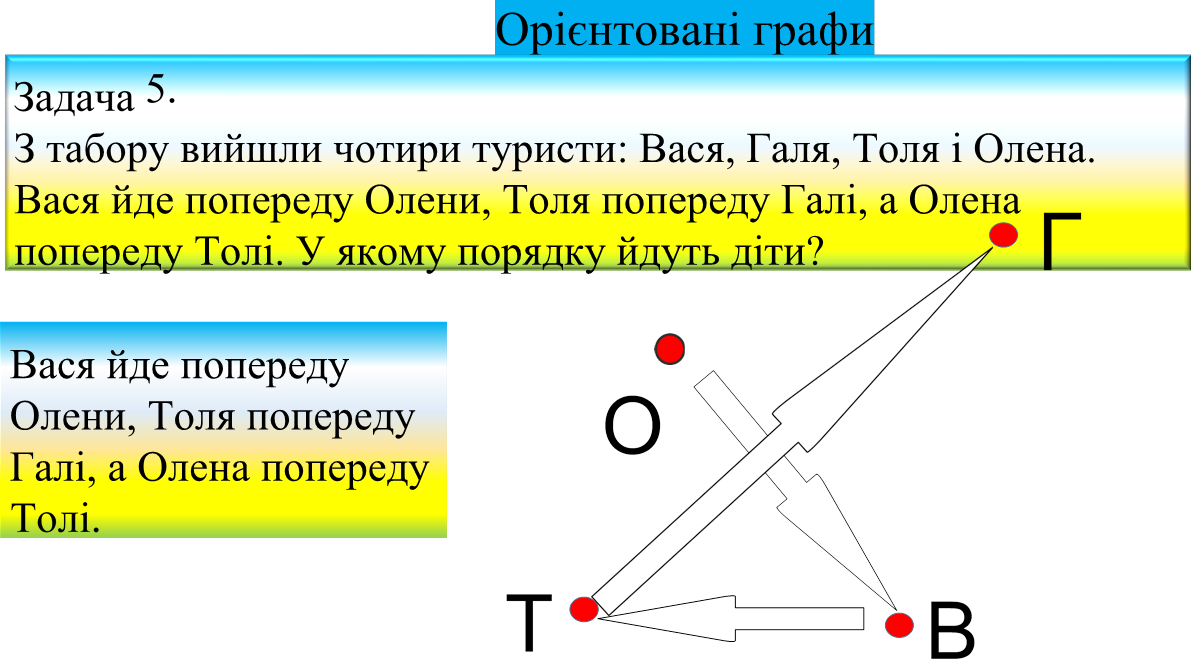
Задача 4.

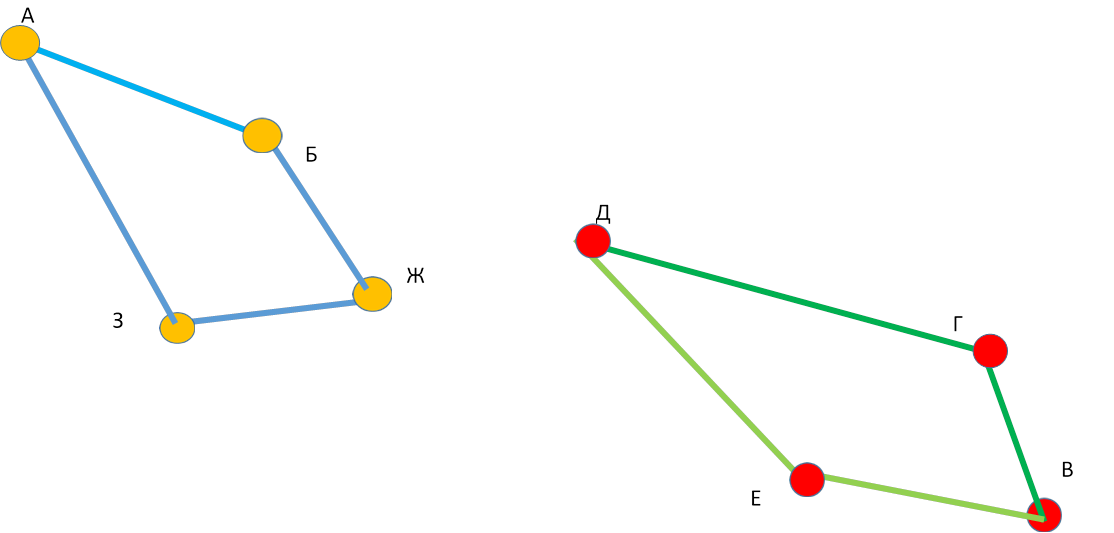
У першості класу з шашок 5 учасників: Аня, Боря, Влад, Гриша, Даша. Першість проводиться за коловою системою - кожен з учасників грає з кожним з інших один раз. До теперішнього часу деякі ігри вже проведені: Аня зіграла з Борею, Владом і Дашею; Боря зіграв, як уже говорилося, з Анею та ще з Грицем; Влад - з Анею і Дашею, Гриша - з Борею, Даша - з Анею та Грицем. Скільки ігор проведено до теперішнього часу і скільки ще залишилося?

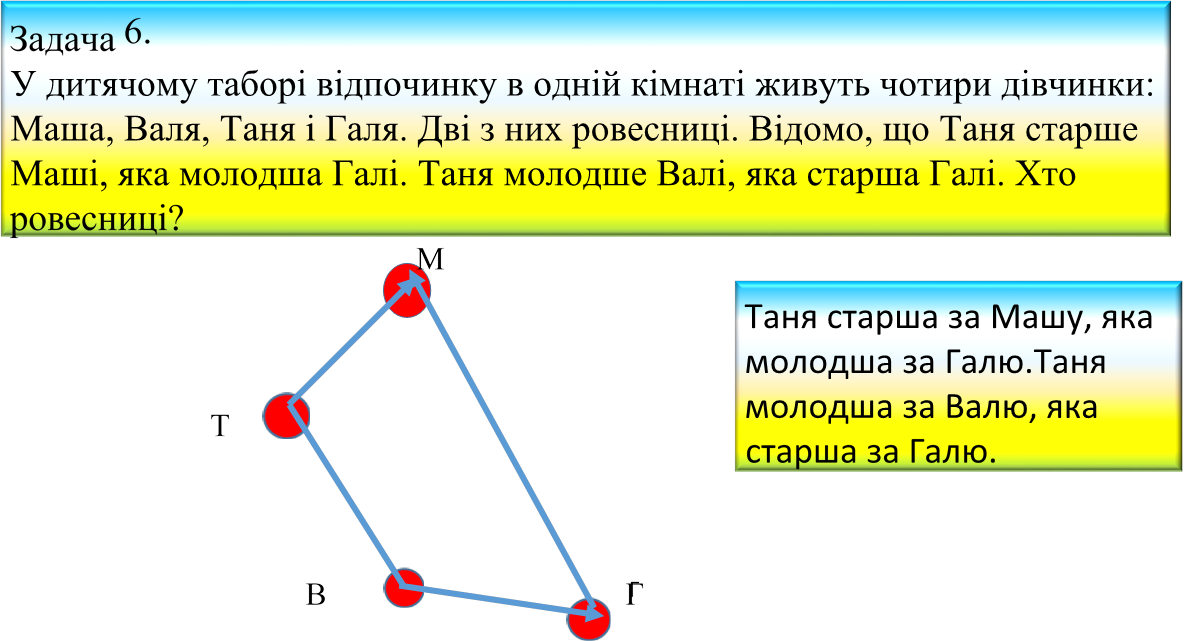
Граф-дерево або дерево можливостей Задача 7.

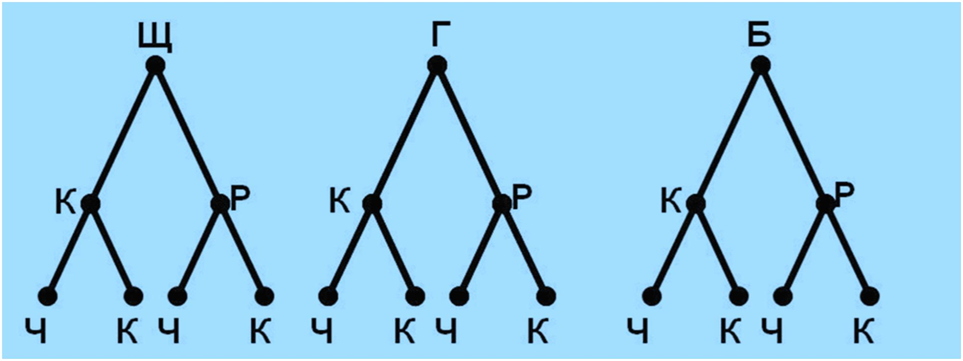
В їдальні на гаряче можна замовити щуку, гриби і баранину, на гарнір - картоплю і рис, а з напоїв - чай і кава. Скільки різних варіантів обідів можна скласти із зазначених страв?

Задача 8.

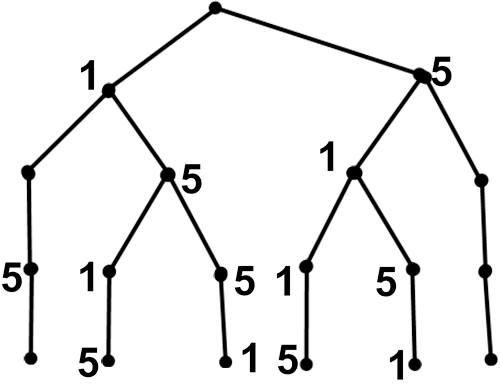
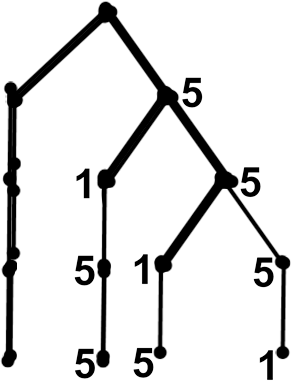
З набірного полотна взяли 2 картки з цифрою 1 і 3 картки з цифрою 5. Скільки різних п'ятизначних чисел можна скласти з цих карток?

                                                                              1                                       5

1

515

51

                                                                                                     55                              1

Граф с ребрами двох кольорів

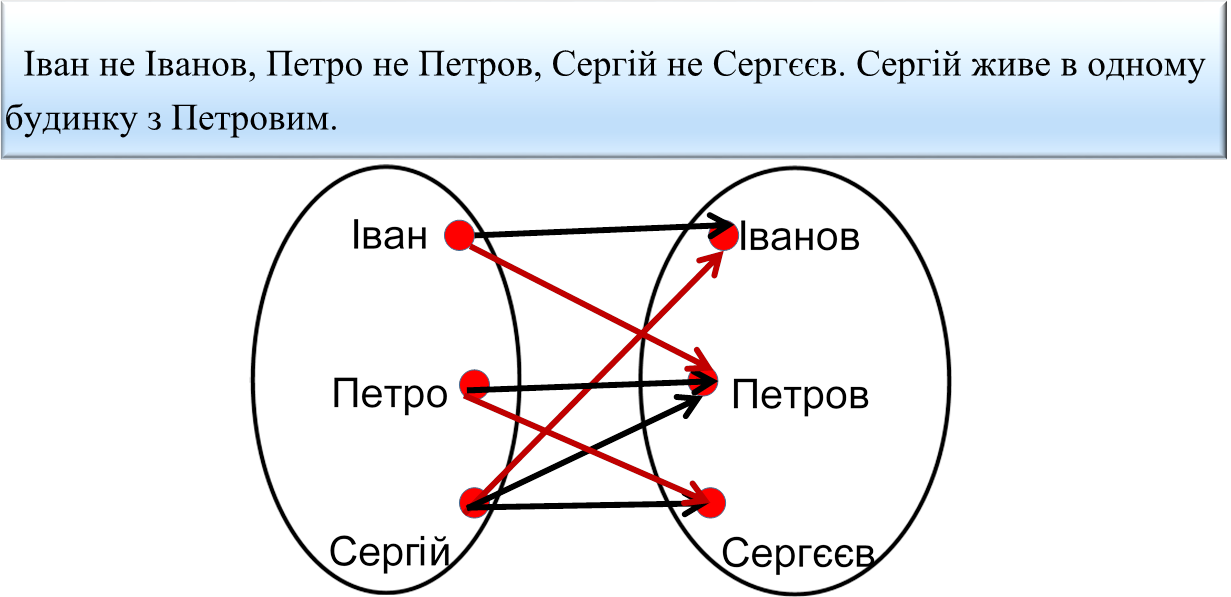
Задача 9. В одному класі вчаться Іван, Петро і Сергій. Їх прізвища Іванов, Петров і Сергєєв. Встанови прізвище кожного з хлопців, якщо відомо, що Іван не Іванов, Петро не Петров і Сергій не Сергєєв і що Сергій живе в одному будинку Петровим.

Граф Петерсена

Задача 10. В деякій державі система авіаліній побудована таким чином, що одне місто з’єднане авіалініями не більше чим з трьома іншими, а також із будь – якого міста в будь- яке інше можна проїхати, зробивши не більше однієї пересадки. Скільки міст  об’єднує дана система авіаліній?

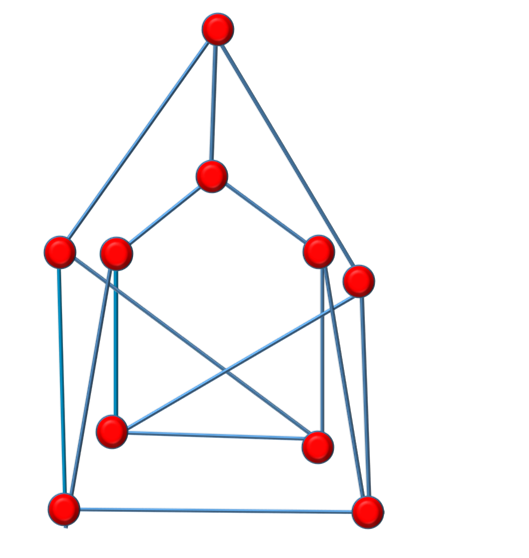Із будь – якого міста А можна добратися не більше, ніж до трьох міст, а із кожного з них не більше, ніж до двох (нерахуючи А). Таким чином, всіх міст не більше 1+3+3*2=10 (міст).

Відповідь: 10 міст.

Таким чином, граф є математичною моделлю найрізноманітних об’єктів, явищ і процесів, що досліджуються і використовуються в науці і практиці. І тому граф є потужним інструментом проникнення математики у всі сфери діяльності. Отже, даний матеріал є актуальним на сьогодні. І тому, на простих ігрових задачах, можна вивчати теорію графів на факультативних заняттях.