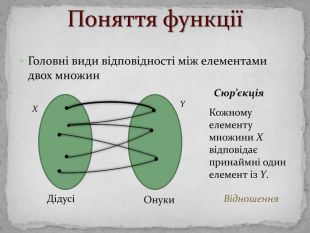
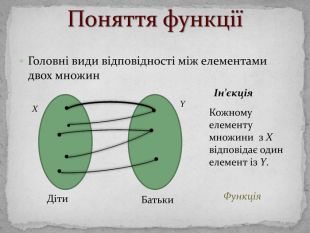
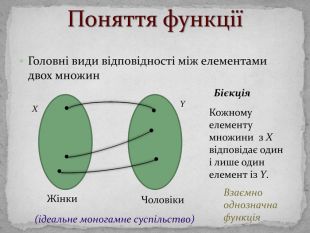
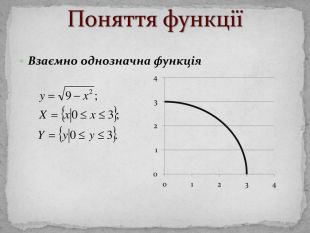
Презинтація з математики "Поняття функції"

вчитель математики. В. М. Галів. Функції

Головні види відповідності між елементами двох множин. Поняття функціїXYСюр’єкція. Кожному елементу множини X відповідає принаймні один елемент із Y. ДідусіОнуки. Відношення

Головні види відповідності між елементами двох множин. Поняття функціїXYІн’єкція. Кожному елементу множини з X відповідає один елемент із Y. Діти. Батьки. Функція

Головні види відповідності між елементами двох множин. Поняття функціїXYБієкція. Кожному елементу множини з X відповідає один і лише один елемент із Y. Жінки. Чоловіки. Взаємно однозначна функція(ідеальне моногамне суспільство)

Відношення. Поняття функції

Функція. Поняття функції

Взаємно однозначна функція. Поняття функції

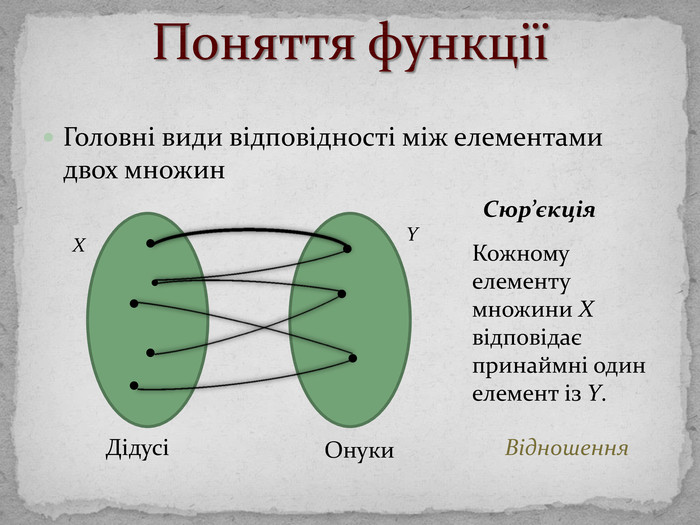
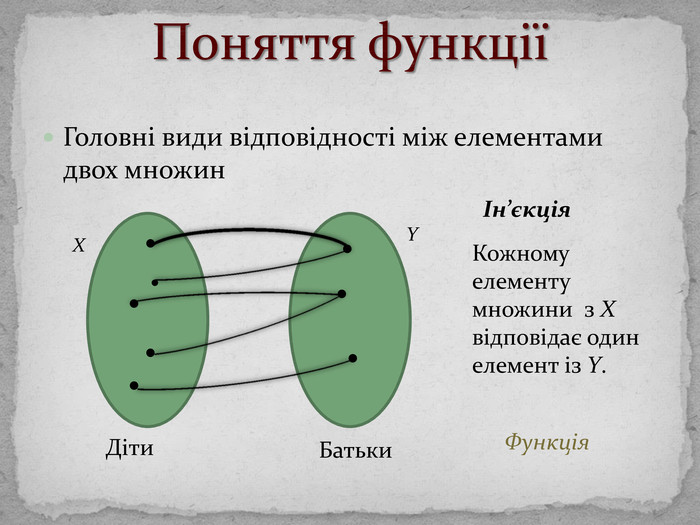
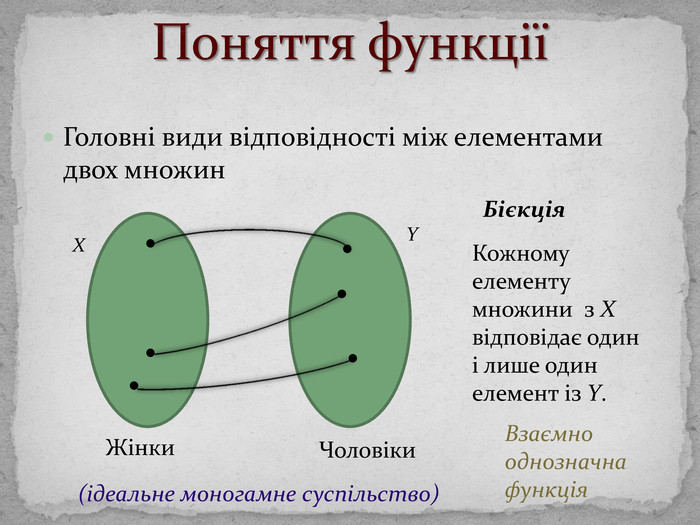
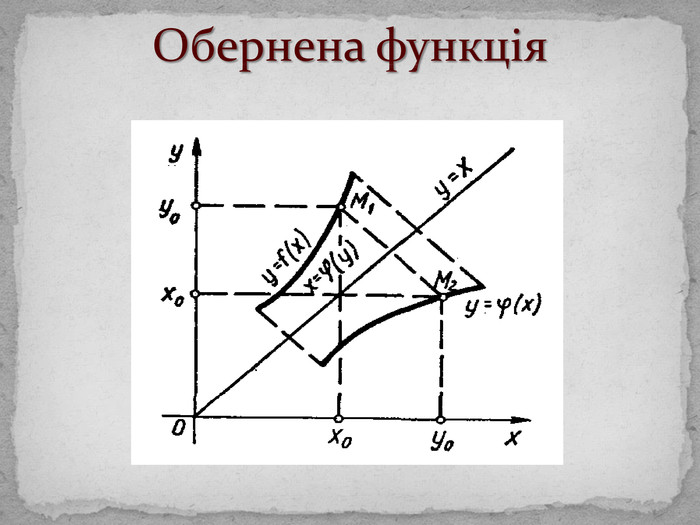
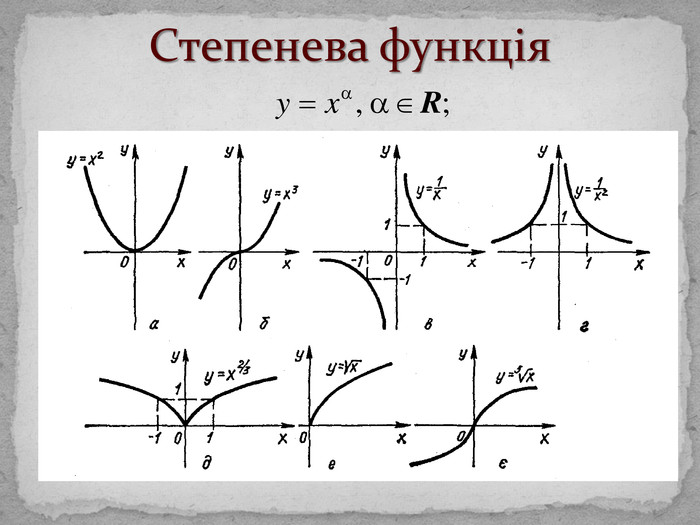
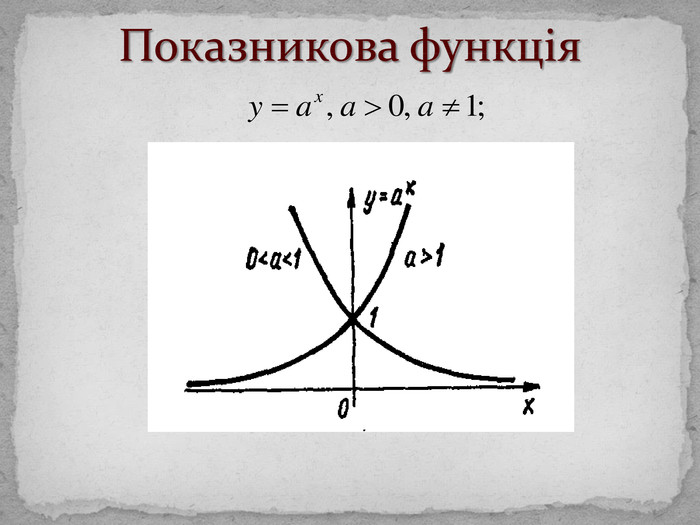
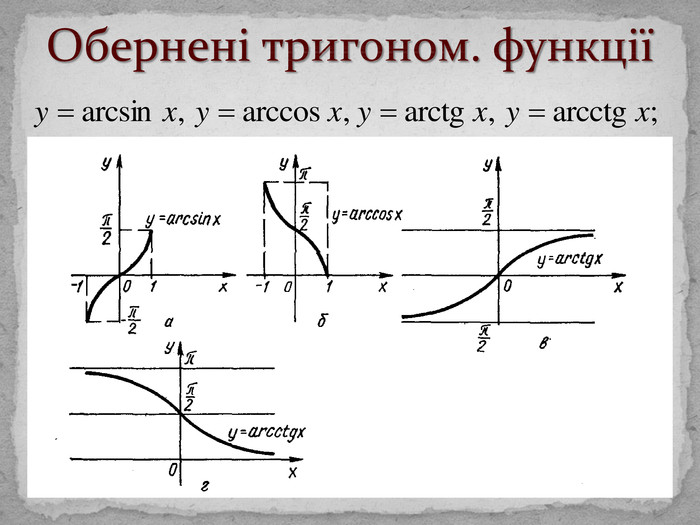
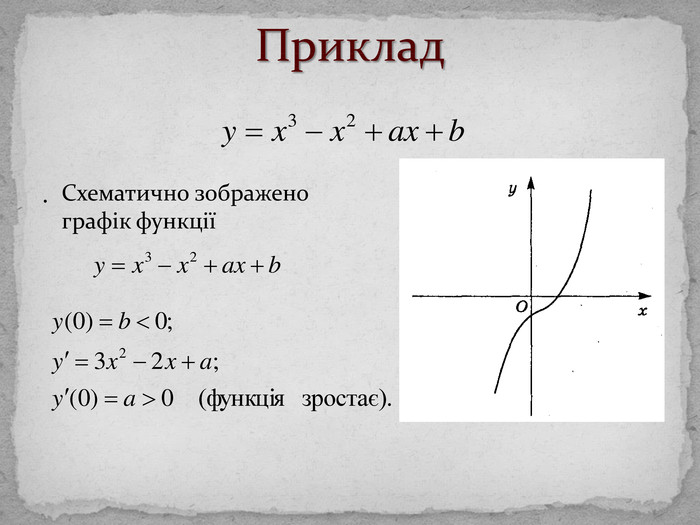
Поняття функціїТермін «функція» вперше ввів Г. Лейбніц. Озн. Функцією називається відповідність, при якій елементу х із множини D відповідає деякий певний елемент y із множини E. D – область визначення функції (позн. D(f)); Е – область значень функції (позн. E(f)). Якщо D(f) і E(f) – числові множини, то функція називається числовою.

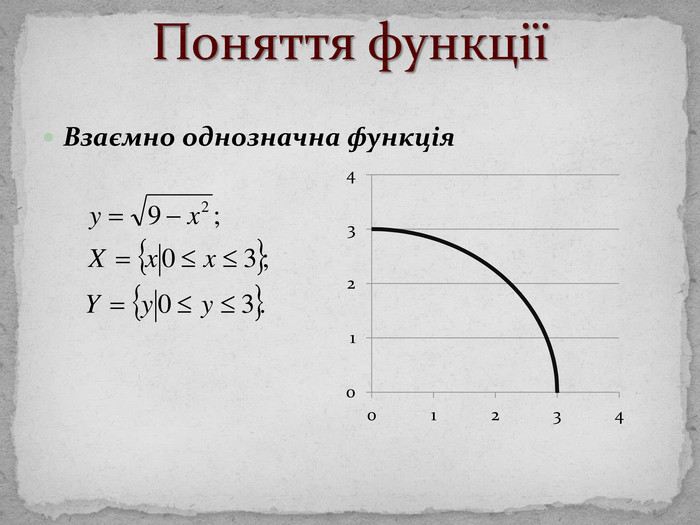
Поняття функціїОзн. Числовою функцією з областю визначення D називається відповідність, при якій кожному числу х  D відповідає деяке цілком означене число y. Озн. (М. Лобачевського і Л. Діріхле) Якщо кожному числу х з деякої числової множини Х за певним правилом поставлене у відповідність єдине число y, то кажуть, що у є функція від х.

Поняття функції

Способи задання функціїФормулою Таблицею Графіком Описом{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}х0123 У0149

Способи задання функції

Властивості функцій. Озн. Функцію y = f(x), визначену на множині Х, називають обмеженою на цій множині, коли існує таке число М > 0, що для всіх х  Х виконується нерівність | f(x)|≤ М.

Властивості функцій. Озн. Функція y = f(x) називається монотонно зростаючою, строго монотонно зростаючою, монотонно спадною, строго монотонно спадною,якщо для кожної пари виконується нерівність: f(x1) ≤ f(x2). f(x1) < f(x2). f(x1) ≥ f(x2). f(x1) > f(x2).

Властивості функцій. Озн. Функція y = f(x) називається парною, непарною, загального виду,якщо для кожного виконується: f(–x) = f(x). f(–x) = – f(x). не виконується жодна умова.(область визначення симетрична відносно точки 0)!

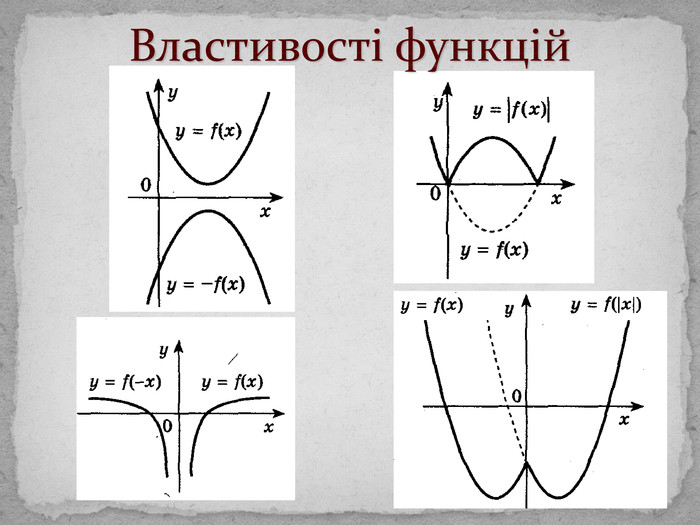
Властивості функцій. Озн. Функція y = f(x), визначена на всій числовій прямій, називається періодичною, якщо існує таке число Т ≠ 0, що f(x + Т) = f(x). Озн. Функція y = f(x), визначена множині Х, називається періодичною на цій множині, якщо існує таке число Т ≠ 0, що х + Т  Х і f(x + Т) = f(x).

Властивості функцій. Озн. Під неявним заданням функції розуміють задання функції у вигляді рівняння нерозв’язаного відносно залежної змінної.

Властивості функцій. Озн. Функція є оберненою до функції , якщо:1) областю визначення функції  є множина значень функції f;2) множина значень функції  є область визначення функції f;3) кожному значенню змінної y  Y відповідає єдине значення змінної x X.

Властивості функцій. Озн. Задання функціональної залежності між х і y у вигляді двох функцій називають параметричним заданням функцій.

Поняття складеної функцій

Елементарні функціїОзн. Основними елементарними функціями називаються такі:1. Лінійна функція2. Степенева функція3. Показникова функція4. Логарифмічна функція5. Тригонометричні функції6. Обернені тригонометричні функціїінші .(Гіперболічні функції )

Лінійна функція

Лінійна функція

Лінійна функція

Лінійна функція

Обернена функція

Степенева функція

Показникова функція

Логарифмічна функція

Тригонометричні функції

Обернені тригоном. функції

Елементарні функцій. Озн. Функції, які дістають з елементарних функцій за допомогою скінченого числа алгебраїчних дій і скінченого числа операцій, що полягають у побудові складної функції, називаються елементарними.

Елементарні функцій Елементарні функціїАлгебраїчні функціїТрансцендентні функціїРаціональні функціїІрраціональні функціїЦіліраціональні функціїДробовіраціональні функції

Елементарні функцій. Перетворення графіків

Елементарні функцій. Перетворення графіків

Деякі неелементарні функцій. Абсолютне значення, або модуль числа

Деякі неелементарні функцій. Ціла частина числа

Деякі неелементарні функцій. Дробова частина числа

Деякі неелементарні функцій. Знак числа

Приклади. Знайти область визначення функції

Приклади. Знайти область визначення функції

Приклади. Знайти область визначення функції 

Приклади. Знайти область значень функції

Приклади. Знайти область значень функції

Приклади. Дослідити на парність функцію

Приклади. Знайти період функції

Обернена пропорційність Озн. Функція виду називається оберненою пропорційністю.

Дробово-лінійна функція

Дробово-лінійна функція. Якщо а = 0: Якщо а = с = 0: Якщо с = 0:

Дробово-лінійна функція. Якщо

Дробово-лінійна функція

Дробово-лінійна функція. Асимптоти:

Дробово-лінійна функція

Дробово-лінійна функція. Пр. Побудувати графік функції1). Функція зростаєАсимптоти

Дробово-лінійна функція. Пр. Побудувати графік функції

Дробово-лінійна функція. Пр. Побудувати графік функції1). Функція зростаєАсимптоти

Дробово-лінійна функція. Пр. Побудувати графік функції1). Функція зростаєАсимптоти

Дробово-лінійна функція. Пр. Побудувати графік функції

Дробово-лінійна функція. Пр. Побудувати графік функції1). Функція спадаєАсимптоти

Дробово-лінійна функція. Пр. Побудувати графік функції

Дробово-лінійна функція. Пр. На рисункузображено графік функціїВизначте знакипараметрів.

Дробово-лінійна функція. Функція спадаєГоризонтальна асимптота. Вертикальна асимптота

Степенева функція

Степенева функція

Степенева функція

Степенева функція

Степенева функція

Степенева функція

Степенева функція

Квадратична функція. Вершина в т. А(m, p), вісь симетрії x = m.

Квадратична функція

Квадратична функція. Якщо ab > 0, (a > 0, b > 0 або a < 0, b < 0, то вісь симетрії знаходиться зліва від осі OY. Якщо ab < 0, (a < 0, b > 0 або a > 0, b < 0, то вісь симетрії знаходиться справа від осі OY.

Квадратична функція. Якщо ab < 0, (a < 0, b > 0 або a > 0, b < 0, то вісь симетрії знаходиться справа від осі OY.

Квадратична функція. Якщо ab > 0, (a > 0, b > 0 або a < 0, b < 0, то вісь симетрії знаходиться зліва від осі OY.

Приклад. Схематично зображено графік функції

Властивості функцій

Приклади. Пр. Побудувати графік функції

Приклади. Пр. Побудувати графік функції

Приклади. Пр. Побудувати графік функції

Приклади. Пр. Побудувати графік функції

Приклади. Пр. Побудувати графік функції

Приклади. Пр. Побудувати графік функції

Приклади. Пр. Побудувати графік функції

Приклади. Пр. Побудувати графік функції

Приклади. Пр. Побудувати графік функції

Приклади. Пр. Побудувати графік функції

Приклади. Пр. Побудувати графік функції

Приклади. Пр. Побудувати графік функції

Приклади. Пр. Побудувати графік функції