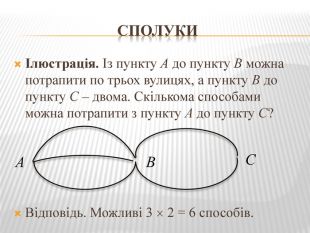
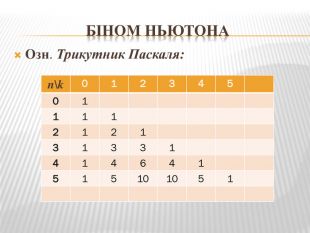
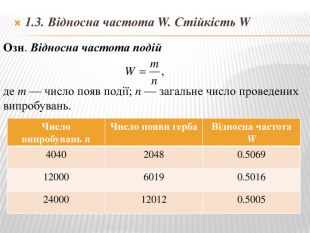
Презинтація з математики "Теорія ймовірності"

Комбінаторика. Озн. Розділ математики, в якому вивчаються методи розв'язування комбінаторних задач, називається комбінаторикою.

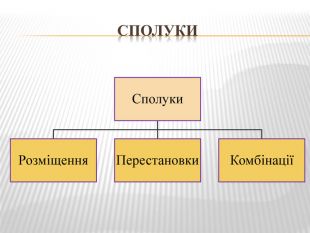
Сполуки. Озн. Різні групи, що утворені з будь-яких елементів або самими елементами, називаються сполуками.

СполукиІлюстрація. Із пункту А до пункту В можна потрапити по трьох вулицях, а пункту В до пункту С – двома. Скількома способами можна потрапити з пункту А до пункту С?Відповідь. Можливі 3  2 = 6 способів. АВС

Сполуки. Пр. Із 10 різних елементів можна скласти групи, по кілька цифр у кожній, наприклад: 123, 312, 9013, 15735 і т. ін. Це різні сполуки із заданих цифр. З них 123 та 312 різняться порядком; 9013 та 15735 – кількістю та складом елементів.

Сполуки. Розглянемо кілька предметів, які об'єднаємо в групи. Ці предмети називатимемо елементами, а групи сполуками. Елементи позначатимемо через

Сполуки. Сполуки, в яких кожен елемент може входити один раз, називають сполуками без повторень. Такими будуть, наприклад,

Сполуки. Сполуки, при складанні яких допускається повторення того самого елемента, називають сполуками з повтореннями. Наприклад, Сполуки, складені з цих елементів, можуть відрізнятися одна від одної кількістю елементів, самими елементами або порядком елементів.

Сполуки

Сполуки без повторень. Озн. Розміщення. Сполуки, які містять однакову кількість елементів і відрізняються одна від одної самими елементами або порядком їх розташування, називають розміщеннями.

Сполуки без повторень. Озн. Перестановки. Сполуки, які містять ті самі елементи і відрізняються одна від одної лише порядком їх розташування, називають перестановками.

Сполуки без повторень. Озн. Комбінації. Сполуки, які містять те саме число елементів, що відрізняються принаймні одним елементом, називають комбінаціями.

Розміщення. Озн. Розміщенням із m елементів по n називають такі впорядковані множини, кожна з яких містить n елементів і які відрізняються між собою порядком розташування цих елементів або хоча б одним елементом.(Озн. Множину називають упорядкованою, якщо при її побудові істотним є порядок розміщення елементів.)

Розміщення. Характеристики:1) предмети і місця різні;2) 0 ≤ n ≤ m;3) усі n місць необхідно зайняти;4) порядок елементів важливий.

Розміщення. Пр. Нехай число предметів, з яких ми складаємо різні сполуки, дорівнює 3. Позначимо їх a, b, c. З них можна скласти такі сполуки:по одному елементу: a, b, c;по два: ab, ac, ba, bc, ca, cb;по три: abc, acb, bac, bca, cab, cba.

Розміщення. Число всіх можливих розміщень з m елементів по n дорівнює добуткові n послідовних цілих чисел, з яких найбільше m. Позначається:

Розміщення. Пр. Маємо дев’ять однакових карток на яких записано цифри 1, 2, …, 9. Скількома способами можна отримати число, що складається з цифр 1, 6, 8, 9?

Розміщення Пр. Скільки способів існує, щоби вибрати з 30 чоловік наукового товариства президента, віце-президента, вченого секретаря?

Розміщення. Пр. Перед випуском група слухачів з 30 чоловік обмінялися фотокарточками. Скільки всього було роздано фотокарток?

Перестановки Озн. Розміщення з m елементів, узятих по m, тобто розміщення, які різняться лише порядком елементів, називають перестановкою..

Перестановки Пр. Скільки чотиризначних чисел можна скласти з цифр 1, 2, 3, 4 без повторень?

Перестановки Пр. Скількома способами можна розмістити 12 осіб за столом, на якому поставлено 12 предметів?

КомбінаціїОзн. Розміщення із m елементів по n у кожній групі, де порядок елементів неістотній, називається комбінацією із m елементів по n.

Комбінації Характеристики:1) предмети різні;2) 0 ≤ n ≤ m;3) порядок елементів неважливий.

КомбінаціїПр. Скільки способів існує, щоби вибрати 3 чергових з 30 учнів.

КомбінаціїПр. Скільки комісій, які складаються із 7 членів, можна створити з 14 вчителів?

Сполуки з повтореннями. Число розміщень з n елементів по p з повтореннями: Число перестановок з повтореннями: Число комбінацій з n елементів по p з повтореннями:

Сполуки з повтореннями. Пр. Зазначте кількість різних слів, які можна скласти з усіх букв слова «математика».«м» — 2 шт.; «а» — 3 шт.; «т» — 2 шт.; «е» — 1 шт.; «и» — 1 шт.; «к» — 1 шт.

Основна формула Комбінаторики. Нехай є k груп елементів, чисельність кожної з яких відповідно дорівнює n1, n2, …, nk. Виберемо довільним чином по одному елементу з кожної групи. Тоді загальне число N способів, якими можна здійснити такий відбір визначається співвідношенням.

Правило суми. Якщо деякий об’єкт А може бути вибраний із сукупності об’єктів n способами, а другий об’єкт В із цієї ж сукупності m способами, то вибрати або А, або В можна n + m способами.

Правило суми. Пр. В одній коробці є 20 пачок печива, а в іншій — 15. Скількома способами можна вибрати одну пачку печива. Відповідь. 35.

Правило добутку. Якщо деякий об’єкт А може бути вибраний із сукупності об’єктів n способами і після кожного такого вибору об’єкт В можна вибрати m способами, то пара об’єктів (А, В) у вказаному порядку може бути вибрана n · m способами.

Правило добутку. Пр. На чергування вибирається два учня – один з трьох, що вчаться в 11 класі, і один з чотирьох, що вчаться у 10 класі. Скільки існує можливих способів формування різних пар з двох учнів? Відповідь. 12.

Комбінаторика. Усі можливі набори з усіх елементів m-елементної множини — різняться лише порядом елементів. Усі можливі набори з n елементів m-елементної множини — різняться або елементами, або їх порядом. Усі можливі набори з n елементів m-елементної множини — різняться лише елементами

Біном ньютона. Озн. Рівність Паскаля:

Біном ньютона. Озн. Трикутник Паскаля:{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}n\k01234501111212131331414641515101051

Біном ньютона. Озн. Формула загального члена розкладу степеня бінома:

Основні формули теорії імовірностей. Озн. Класичне означення ймовірностіде m – число елементарних випадків, що сприяють появі події А; n – загальне число всіх єдино можливих, рівно можливих і несумісних подій.

Основні формули теорії імовірностей. Озн. Відносна частота подійде m — число появ події; n — загальне число проведених випробувань.

Основні формули теорії імовірностей. Теорема додавання ймовірностейа) для несумісних подійб) для сумісних подій

Основні формули теорії імовірностей. Сума ймовірностей протилежних подійде – подія, протилежна до події А.

Основні формули теорії імовірностей. Теорема множення ймовірностейа) для незалежних подійб) для залежних подійде – умовна ймовірність події В.

Основні формули теорії імовірностей. Ймовірність появи хоча б однієї із n незалежних подій А1, А2, …, Аn:де – ймовірності подій Якщо події – мають однакову ймовірність p, то

Основні формули теорії імовірностей. Ймовірність появи однієї із трьох подій А1, А2, А3:де – ймовірності подій

Основні формули теорії імовірностей. Ймовірність появи події k-раз в n-випробувань. Формула Бернуллі:

Випадкові події1.1. Випадкові події. Класифікація подій. 1.2. Класичне означення ймовірності.1.3. Відносна частота. Стійкість відносної частоти.1.4. Статистичне означення ймовірності.1.5. Геометричне означення ймовірності.

1.1. Випадкові події. Класифікація подій Озн. Послідовність операцій, виконуваних з додержанням певного комплексу умов, називають експериментом (випробуванням, дослідом). Озн. Наслідок будь-якого експерименту називають подією. Події поділяються на вірогідні, неможливі та випадкові.

1.1. Випадкові події. Класифікація подій Озн. Якщо в результаті експерименту певна подія обов’язково настане, то вона називається вірогідною. Позначається Ω. Озн. Подія називається неможливою, якщо в результаті експерименту вона не настає ніколи. Позначається .

1.1. Випадкові події. Класифікація подій Озн. Подія називається випадковою, якщо у результаті експерименту вона може настати або не настати. Позначаються А, В, С…Озн. Події називаються несумісними, якщо поява однієї із цих подій виключає появу другої події в одному і тому ж випробуванні. Озн. Якщо поява однієї події не виключає появу іншої, то такі події називаються сумісними.

1.1. Випадкові події. Класифікація подій Озн. Події називаються рівноможливими, якщо ні одна з них подій не має «переваги» над іншою. Озн. Події попарно несумісні і рівноможливі, утворюють повну групу подій, із яких хоч би одна неминуче відбудеться (тобто сума цих подій є подія достовірна).

1.1. Випадкові події. Класифікація подій Озн. Подія, що може відбутися внаслідок проведення однієї і лише однієї спроби називається елементарною (простою) випадковою подією. Озн. Подія називається складеною, якщо її можна розкласти на прості події.

1.1. Випадкові події. Класифікація подій Озн. Сумою двох подій А і В називається така подія С (С = А + В), яка внаслідок експерименту настає з настанням принаймні однієї з подій А або В. Озн. Добутком двох подій А і В називається така подія С (С = А · В), яка внаслідок експерименту настає з одночасним настанням подій А і В. Озн. Різницею двох подій А і В називається така подія С (С = А \ В), яка внаслідок експерименту настає з настанням події А і одночасним ненастанням події В.

1.2. Класичне означення ймовірності Озн. Класичне означення ймовірностіде m – число елементарних випадків, що сприяють появі події А; n – загальне число всіх єдино можливих, рівно можливих і несумісних подій.

1.3. Відносна частота W. Стійкість W Озн. Відносна частота подійде m — число появ події; n — загальне число проведених випробувань. {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Число випробувань n. Число появи герба. Відносна частота W404020480.50691200060190.501624000120120.5005

1.4. Статистична ймовірність W(А) Озн. Статистична ймовірністьде m – число появ події; n – загальне число проведених випробувань.

1.5. Геометричне означення ймовірності Озн. Геометрична ймовірністьде mes(A) – міра області, яка сприяє події А, mes() – міра всієї області.

Основні теореми2.1. Теорема додавання ймовірностей. 2.2. Протилежні події.2.3. Умовна ймовірність.2.4. Теорема множення ймовірностей.2.5. Ймовірності появи хоча б однієї події.2.6. Незалежні випробування. Схема Бернуллі.

2.1. Теорема додавання ймовірностей Приклад. У коробці знаходяться 30 куль. Із них 10 червоних, 5 синіх і 15 білих. Із коробки навмання виймають кулю. Знайти ймовірність того, що вийнята куля кольорова.

2.2. Протилежні події Приклад. Два кубики кидають один раз. Знайти ймовірність того, що хоча б один раз випаде 6 очок. А – випаде 6 очок на першому кубику;В – випаде 6 очок на другому кубику. (А і В – сумісні).

2.3. Умовна ймовірність Приклад. Кидаємо кубик, грані якого пронуме-ровані. Нехай подія А полягає в тому, що випадає парне число, В — випаде число більше від одиниці.

2.3. Умовна ймовірність Приклад. В урні містяться 6 білих і 4 чорних кулі. Із урни два рази виймають по одній кулі. Знайти ймовірність того, що за другим випробуванням буде вийнята біла куля (подія В), якщо першою була вийнята чорна куля (подія А).

2.4. Теорема множення ймовірностей Приклад. З ящика, який містить 5 білих і 3 чорних вироби, виймають навмання два вироби. Яка ймовірність того, що обидва білі?А – поява білого виробу при першому вийманні,В – поява білого виробу при другому вийманні.

2.4. Теорема множення ймовірностей Приклад. Задані числа від 1 до 9. Навмання беруть одне число, а далі з решти — друге. Знайти ймовірність, що отримане двоцифрове число буде парним. А – поява непарної цифри при першому вийманні,В – поява парної цифри при першому вийманні,С – поява парної цифри при другому вийманні

2.4. Теорема множення ймовірностей Приклад. В ящику 5 білих, 4 чорних, 3 синіх вироби. Виймаються по одному виробу, не повертаючи назад. Знайти ймовірність того, що при першому вийманні з’явиться білий виріб (подія А), другому – чорний (подія В), третьому – синій (подія С).

2.4. Теорема множення ймовірностей Приклад. Задано числа від 1 до 13. Яка ймовірність того, що взяте число виявиться кратним 3, коли відомо, що воно парне?

2.4. Теорема множення ймовірностей Приклад. Знайти ймовірність попадання в ціль двома спортсменами, якщо ймовірність попадання першого – 0,6 (подія А), другого – 0,8 (подія В).

2.5. Ймовірності появи хоча б однієї події Приклад. Ймовірність влучання в ціль із трьох рушниць, відповідно дорівнює p1=0,7, p2=0,8, p3=0,9. Знайти ймовірність хоч би одного влучання (подія А) при одному залпі із трьох рушниць.

2.5. Ймовірності появи хоча б однієї події Приклад. Знайти ймовірність того, що при восьми киданнях монети принаймні один раз випаде герб.

2.5. Ймовірності появи хоча б однієї події Приклад. У люстрі 4 лампи. Ймовірність невиходу з ладу за певний проміжок часу для кожної лампи дорівнює p. Визначити ймовірність справної роботи люстри протягом цього часу (її надійність). Скільки ламп повинна мати люстра, щоб надійність перевищувала 0,99 за умови, що p = 0,8.

2.6. Незалежні випробування. Схема Бернуллі Нехай здійснюється n незалежних випробувань, причому ймовірність появи подій А в кожному випробовуванні вважається постійною і дорівнює p. Відповідно, імовірність не появи події А в кожному випробовуванні також постійна і рівна q (лише два несумісні наслідки). Простір елементарних подій для n експериментів – 2n елементарних подій. Випробовування називають незалежним, якщо ймовірність появи випадкової події А кожному з них не залежить від результатів інших випробовувань.

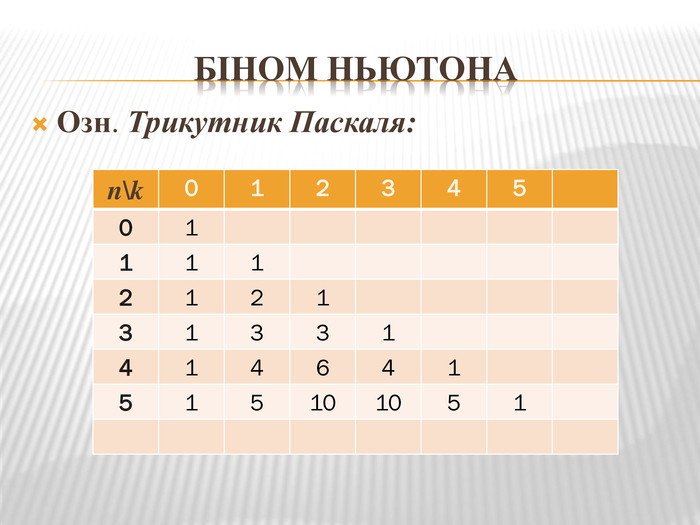
2.6. Незалежні випробування. Схема Бернуллі Задача. Обчислити ймовірність того, що при n випробовуваннях випадкова подія настане рівно k і, відповідно, не настане n – k раз. Позначимо шукану ймовірність Pk,n або Pn(k). Зауважимо, що не враховується послідовність появи події А. Наприклад, поява події А два рази у трьох випробовуваннях рівносильна складеним подіям ААĀ, АĀА, ĀАА. Ймовірність Pn(k) залежить від двох параметрів n, p.

2.6. Незалежні випробування. Схема Бернуллі Приклад. Спортсмен стріляє три рази. Ймовірність кожної спроби постійна і дорівнює p. Знайти ймовірність успішного завершення двох спроб з трьох. Розв’язання. Нехай A1, A2, A3 – успіх в першій, другій, третій спробі. Тоді дві успішні спроби відповідають наступним подіям А1 А2Ā3, А1Ā2 А3, Ā1 А2 А3.

2.6. Незалежні випробування. Схема Бернуллі Подію, що нас цікавить можна записати як суму А1 А2Ā3+А1Ā2 А3+Ā1 А2 А3. Так як події, що входять в цю суму не сумісні, а події A1, A2, A3 незалежні то за формулами додавання і множення знаходимо

2.6. Незалежні випробування. Схема Бернуллі Монету підкидають 10 раз. Яка ймовірність, що при цьому герб випаде рівно 3 рази?

2.6. Незалежні випробування. Схема Бернуллі В урні 20 куль: 15 білих і 5 чорних. З урни послідовно беруть 5 куль, причому кожну взяту кулю повертають в урну перед наступною спробою. Знайти ймовірність того, що з 5 куль 2 будуть білі?

2.6. Незалежні випробування. Схема Бернуллі Імовірність того, що лампочка не перегорить, є величиною сталою і дорівнює 0,9. Обчислити ймовірність того, що з п'яти лампочок не перегорять не менш як дві.

1.5. Геометричне означення ймовірності Озн. Геометрична ймовірністьде mes(A) – міра області, яка сприяє події А, mes() – міра всієї області.

1.5. Геометричне означення ймовірності Приклад 1. Між 0 і 1 навмання вибрано два числа x і y. Знайти ймовірність того, що сума цих чисел не більше, ніж 1, а модуль різниці не менше, ніж 0,5.

1.5. Геометричне означення ймовірності Приклад 1. Між 0 і 1 навмання вибрано два числа x і y. Знайти ймовірність того, що сума цих чисел не більше, ніж 1, а модуль різниці не менше, ніж 0,5.

1.5. Геометричне означення ймовірності Приклад 2. Між числами −1 і 1 навмання вибирають два числа. Знайти ймовірність того, що сума квадратів цих чисел буде не більше 1.

1.5. Геометричне означення ймовірності Приклад 3. Між числами 0 і 1 навмання вибирають два числа x і y. Знайти ймовірність того, що y ≤ x².

1.5. Геометричне означення ймовірності Приклад 4. Навмання вибрано два числа −1 ≤ x ≤ 1, і 0≤ y ≤ 2. Знайти ймовірність того, що y ≥ 2x².

1.5. Геометричне означення ймовірності Приклад 5. Навмання вибрано два числа 0 ≤ x ≤ 1, і 0≤ y ≤ 1. Яка ймовірність того, що їх сума не більше одиниці, а сума їх квадратів не менше 0,25.