Прикладні задачі з математики

ЗАДАЧА 1

Для обкладання приміщення полістирольними плитками необхідно 200кг каніфольної мастики, яка має склад у частках:

• Каніфоль – 1.7
• Спирт – 1.1
• Оліфа оксоль - 0.7
• Вапняна мука -6.5

Наповнювач (вапняна мука) у мастиці має становити не менше ніж 65%, а розчинник – не більше ніж 12%. При порушенні цих пропорцій мастика розшаровується. Скільки кілограмів кожної речовини потрібно для виготовлення 200кг мастики?

 

РОЗВ’ЯЗАННЯ

 

1) Знаходимо, скільки всього частин припадає на 200 кг мастики

1,7+1,1+0,7+6,5=10

2) Знаходимо масу яка припадає на одну частину:

 200 : 10 = 20(кг)

3) Знаходимо масу кожної речовини:

 Каніфоль: 1,7*20 = 34 (кГ)

 Спирт : 1,1 * 20 = 22 (кг)

 Оліфа : 0,7 * 20 = 14 (КГ)

 Вапняна мука: 6,5*20=130 (КГ)

4) Перевіряємо виконання необхідних пропорцій:

 200-100%

 Х – 65%

 

 200-100%

 Х-12%

 

 Необхідна пропорція збережена.

 У рецепті вказано 22кг, що менше ніж 24 кг, із чого випливає що необхідна пропорція витримана.

ВІДПОВІДЬ: Для одержання 200 кг мастики необхідно: каніфолі 34кг; спирту 22кг; оліфи 14кг; вапняної муки 130кг; Майбутні плиточники повинні вміти розрахувати кількість плитки необхідні для обкладання ладанної поверхні.

ЗАДАЧА 2

 

Визначити площу керамічної плитки й кількість плитки необхідної для обкладання підлоги що має форму шестикутника розміром 2,3 х 3,1м якщо плитка має форму правильного шестикутника зі стороною а=0,25м

 

РОЗВ’ЯЗАННЯ

1) Для обчислення площі плитки використовуємо формулу для обчислення площі правильного шестикутника:

 

2) визначити площу підлоги

 2,3*3,1=7,13

3) Визначити необхідну кількість плитки:

 

ВІДПОВІДЬ: Для обкладання підлоги потрібно не менше 99 плиток.

У цій задачі, крім того що, використовується формула площі правильного шестикутника, необхідні знання дій з дійсними числами.

 Наступна задача розвиває в учнів логічне мислення та сприяє вмінню учнів ефективно й економно використовувати у своїй роботі потрібні матеріали.

 

ЗАДАЧА 3

 

Із круглої колоди діаметром d необхідно вирізати стойку прямокутного перерізу з найбільшою площею "Стойка - Елемент", який працює на стискання. Найбільша площа перерізу балки необхідна для сприяння найбільшого навантаження.

 

 

 

 

 

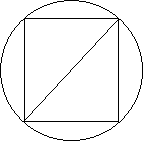
Мал.

 

РОЗВ’ЯЗАННЯ:

1) Визначимо сторони прямокутника х та у. Тоді за теоремою Піфагора :

 .

2) Площу прямокутника визначимо за формулою:

 .

3) знайдемо похідну площі прямокутника

 

4) визначити нулі функції  

 

 

 

5) Так як х - довжина прямокутника х більше 0, тому досліджуємо лише один корінь.

у точці     похідна замінює знак Із "+" на "-" отже у цій точці - максимум оскільки в нас лише одна екстремальна точка - у цій точці функція приймає найбільшого значення. Тому при  і   найбільша площа .

 

ВІДПОВІДЬ: Переріз балки повинен мати форму квадрата із стороною .

Для розв’язання  наступної задачі учні повинні вміти робити ескіз потрібної фігури. Застосування набутих навичок при розв’язуванні задачі сприяє розвитку просторової уяви та естетичних смаків.

 

ЗАДАЧА 4

 

Для обкладання підлоги є плитка основного тону й фризова. При чому плитки основного тону більше. при укладанні фризової плитки у формі прямокутника його периметр - 10м . Яким за розміром повинні бути сторони прямокутника щоб кількістю фризової плитки яка є в наявності обмежити найбільшу поверхню підлоги?

  ПРИМІТКА Малюнок підлоги вибирають з урахуванням розміру і призначення приміщення . Фон підлоги добре обмежується фризовими рядами в які вкладають плитки більш темних кольорів або спеціальні фризові плитки.

 

 

 

 

 

 

РОЗВ’ЯЗАННЯ:

 

1) Позначимо сторони фризового прямокутника:

 AB=x;  AD=y;

2) Знаходимо периметр:

P=2(x+y);  10=2x+2y;  5=x+y;   y=5-x;

3) Виразимо площу прямокутника через:

S=x*y=x (5-x)=5x-

4) Знайдемо похідну:

 

5) Визначимо критичні точки:

 

 

6)  Визначимо змінну знака в критичній точці:

 Похідна в точці змінює знак із «+» на «-», отже при функція приймає найбільшого значення. При функція приймає найбільшого значення. При  ;

ВІДПОВІДЬ: Фризову плитку економніше викласти у формі квадрата зі стороною 2,5 м.

 

У практиці будівництва довжину лінії на площині вимірюють за допомогою стрічки, дроту, рулетки. Часто виміри необхідно виконувати на нахиленій площині, при цьому визначають величину проекції цієї лінії на горизонтальній поверхні.  Для цього одержане значення вводять поправку на нахил лінії де h – перевищення одного кінця стрічки до другого; l – довжина вимірювальної лінії.

 

ЗАДАЧА 5

Завіси даху утворюють прямокутник ABCD. AB=12м  BC=30м; кут нахилу скатів 30 градусів. Довести що нахили скатів рівні. Знайти площу поверхні покрівлі? Мал. 1

 

 

 

 

 

 

 

 

 

РОЗВ’ЯЗАННЯ:

1) Скати даху представляють собою рівні прямокутники BCFE і ADFE .

2) Прямокутник ABCD розташований горизонтально.

3) Площина трикутника  ABE і CDF перпендикулярна до площини ABCD.

4) Так як скати даху - прямокутники EF паралельна AD. Отже за ознакою паралельності прямої й площини EF паралельна площині ABCD.

5) Скат BCFE утворює двогранний кут , ребро якого BC. Побудуємо лінійний кут двогранного кута. Проведемо EК перпендикулярно AB, оскільки ABЕ перпендикулярний ABCD, то ЕК перпендикулярно ABCD. Похила ВЕ перпендикулярна ВС, отже, її проекція ВК перпендикулярна ВС. Отже кут АВЕ = β – лінійний кут двогранного кута, який утворений скатом BCFE і площиною ABCD.               Аналогічно можна довести що кут ЕАВ дорівнює куту ЕАВ- лінійний кут двогранного кута,  який утворений скатом AEDF і площиною ABCD.

6) Розглянемо трикутник ABE, він рівнобедрений, отже, кут ЕАВ дорівнює куту ВАЕ тому вони - рівні й двогранні кути. Отже, скати даху нахилені до горизонталі однаково.

7) 

 

   2*30*6.93=415.81

ВІДПОВІДЬ:

 

ЗАДАЧА №6

 

На скільки збільшиться вартість штукатурки в даному приміщенні, якщо товщину штукатурного намету збільшити на 2мм; на 5см;

 Примітка: вартість одного мм штукатурного намету на 1м – 5 гр.

 

 

 

 

 

 

 

 

РОЗВ’ЯЗАННЯ:

1) Визначити площу яку необхідно відштукатурити:

 

2) Якщо шар штукатурки  збільшити на 2мм і відомо що вартість штукатурки на 1 м становить 5грн то одержимо: (грн.)

3) Якщо шар штукатурки збільшити на 5мм, то: (грн.)

Відповідь:При збільшенні шару штукатурки на 2 мм вартість штукатурних робіт збільшиться на 357,5 грн. При збільшенні шару штукатурки на 5мм вартість штукатурних робіт збільшиться на 893.75 грн.

 

ЗАДАЧА №7

 

На скільки збільшиться вартість штукатурки в даному приміщенні, якщо товщину штукатурного намета збільшити на 2 мм; на 5 мм?

Примітка. Вартість одного міліметра штукатурного намета на 1 м² - 5 коп.

 

 

РІШЕННЯ:

1. Визначимо площу, яку потрібно поштукатурити:

S= 2 • / AB  +  BC/ • AA_I = 2 • / 2,5 + 4/ • 2,75 = 35,75 м².

2. Якщо шар штукатурки збільшиться на 2 мм і відомо, що вартість штукатурки на 1 м2 становить 5 коп.

С₁=35,75 • 2 • 5 = 357,5 /коп./ = 3, 58 /руб./

3. Якщо шар штукатурки збільшиться на 5 мм, то:

С₂=35,75 • 5 • 5 = 893,75 /коп./ = 8, 94 /руб./

ВІДПОВІДЬ: При збільшенні шару штукатурки на 2 мм, вартість штукатурних робіт в даному приміщенні збільшиться на 3 руб 58 коп.

 При збільшенні шару штукатурки на 5 мм, вартість штукатурних робіт збільшиться на 8 руб 94 коп.

 

ЗАДАЧА №8

 

Визначити масу піску, придатного для мозаїчних робіт, складеного в купу, що має форму усіченої піраміди, якщо об'ємна маса його становить 1600 кг/м³.

 

 

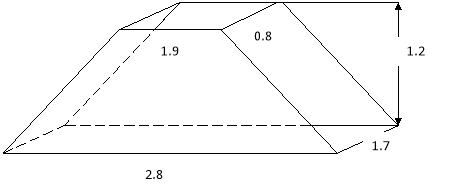
РІШЕННЯ:

1. Знайдемо площу верхньої основи:

Q = 1,9 • 0,8 = 1,59 м²

2. Визначимо площу нижньої основи:

q = 2,8 • 1,7 = 4,76 м²

3. Об’єм складе:

V = • 0,6= 3,768 м³

4. Знайдемо масу піска:

М= Vm_v = 3?768 • 1600 = 6028,8 кг.

ВІДПОВІДЬ: Маса піска дорівнює 6028,8 кг.

ЗАДАЧА № 9

 

Є водопровідні труби діаметром 25, 32, 50, 70 мм. На будівельний майданчик необхідно подавати 10 м³ води за годину. Швидкість течії води в трубах 1,5 м / сек. Визначити діаметр труби водопроводу.

 

 

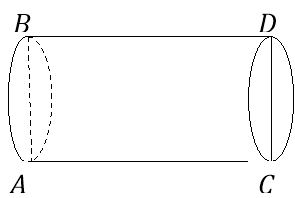
РІШЕННЯ:

1. Розглянемо частину труби довжиною 1,5 м, тому що швидкість течії води 1,5 м / сек. Отримав циліндр висотою АС = 1,5 м і діаметром Д.
2. Визначимо об'єм води, що протікає в трубі за секунду:

V=

3. На будівельний майданчик має подаватися 10 м3 води за годину, що складе в секунду:

= м³/сек.

4. Знайдемо діаметр труби:                                                          

=

Д2 = = 0, 0023 м³

Д = = 0,0023 = 0,0485 м = 48,5 мм.

 

ВІДПОВІДЬ: Водопровідні труби повинні бути діаметром 50 мм.

 

 

ЗАДАЧА № 10

 

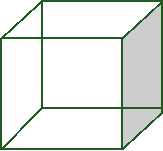
 Потрібен поштукатурити дві колони однакової висоти: а) круглого перерізу з діаметром - 30см; б) квадратного перетину із стороною - 30см. На отштукатуріваніе який колони піде більше матеріалу і в скільки разів?

 

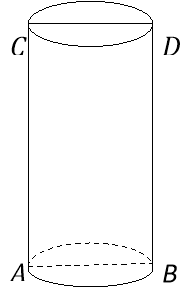
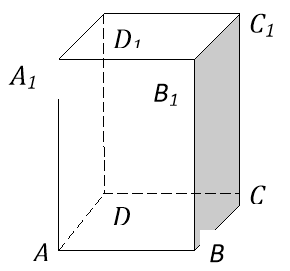
РІШЕННЯ:

1. Знайдемо площу поверхні колони з круглим перерізом:

S_кр = Р_осн • Н = 94,2 Н

 

2. Знайдемо площу поверхні колони з квадратним перетином:

S_кв = Р_осн • Н = 120 Н

 

3. Визначимо у скільки разів S_кр < S_кв

= = 1,3 раза

 

ВІДПОВІДЬ: На колону з квадратним перетином піде штукатурки в 1,3 рази більше, ніж на колону з круглим перетином.

 

ЗАДАЧА № 11

Знайти масу піску, придатного для мозаїчних робіт, якщо він зсипають у купу, що має форму конуса діаметром 3м і висотою 1,4 м. Об'ємна маса піску 1700 кг/м³, вологість піску 7-8%, а при такій вологості його обсяг треба зменшити на 15%.

 

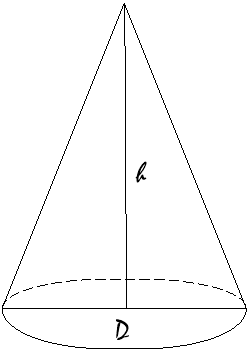
РІШЕННЯ:

1. Масу піску в купі конусоподібної форми в будівництві обчислюють за формулою:

V = 0,262Д²Н, вытекающей на

V=

делением  = 0,262.

2. Знайдемо об’єм  конуса::

V = 0,262 • 3² • 1,4 = 3,3 м³

3. Зменшим об’єм на 15%:

V₁ = = 2,8 м³

4. Знайдем масу піска:

M = m_пV₁ = 2,8 • 1700 = 4740 кг

    ВІДПОВІДЬ:  Маса піску состави 4760 кг.

 

ЗАДАЧА №12

 

У 2009 році всі вклади населення у банку дорівнювали 10млн.грн а норми обов’язкового резервування становили 20%. Скільки кредитів міг надати банк у 2009 році?

 

РОЗВЯЗАННЯ:

Обов’язковий резерв дорівнює :

1. 10 000 000 * 0,2 = 2 000 000грн;
2. 10 000 000 – 2 000 000 = 8 000 000 грн. - гроші які банк може надати у вигляді кредиту .

 

ВІДПОВІДЬ: 8 000 000 грн. гроші які банк може надати у вигляді кредиту.

 

ЗАДАЧА №13

 

Банк залучив вклади від населення на суму 500 тис. грн. під 25% річних і всі ці кошти надав у позику клієнтам під 40% річних. Чому дорівнює прибуток банку?

 

РОЗВЯЗАННЯ

1. 500 000 * 0,40 = 200 000грн. – сума, що одержить банк за надання кредитів.
2. 500 000 *0,25 = 125 000 грн. - відсотки що повинен сплатити банк вкладникам.
3. 200 000 – 125 000 = 75 000 грн. - прибуток банку.

 

ВІДПОВІДЬ:  75 000 грн. - прибуток банку.

ЗАДАЧА №13

 

Ви учні виграли у лотерею 1000 гривень. Поруч із вашим Ліцеєм розташований банк «Приват»  який приймає вклади під 20% річних шляхом нарахування «простого відсотка» . Яку суму отримають учні якщо вкладуть гроші до кінця 2 го го курсу?

 Простий відсоток нараховується за формулою: S=P(1+ni).

 

РОЗВЯЗАННЯ

 Р=1000 грн.; S=1000(1+0.2*2)=1000*1.4=1400грн.; n = 2 роки; i = 0,2;  S-?;

ВІДПОВІДЬ: Учні отримають 1400 гривень.

 

ЗАДАЧА №15

 

Учень звернувся до банку за кредитом у 100 000 гривень, на два роки. Вам запропонували 2 варіанти: або 60% простих річних відсотків, або 40% складних.

 Який варіант вам варто обрати?

 

РОЗВЯЗАННЯ:

Р=100 000грн. S=P(1+ni). – простий відсоток.

 n = 2 роки;

i = 0,6;   S=P(1+i)2 – Складний відсоток.

I = 0,4;   S= 100 000(1+0,4)2=196 000грн.

  S-?

ВІДПОВІДЬ: Варто взяти кредит під складний відсоток.

 

ЗАДАЧА №16

До двадцятиріччя сина батьки відкрили на його ім’я ощадний рахунок у сумі 6 000 гривень. Який повинен бути банківський відсоток щоб до 25 – річчя сума на рахунку подвоїлася?

 

 

 

ЗАДАЧА №17

 

Для приготування 3х літрів борщу необхідно 20г провареної солі (NaCl) вирахувати відсотковий склад солі у борщі.

  

 

 

ВІДПОВІДЬ: у 3х літрах борщу вміст солі дорівнює .

 

ЗАДАЧА №18

 

Для приготування картопляного пюре на одну порцію необхідно 500 грамів картопляної маси. Скільки картоплі потрібно заготувати для приготування 100 порцій на протязі 6 місяців при умові що 20%відходів картопляної маси?

 

РОЗВЯЗАННЯ:

1. Маса пюре 0,5*100*180=900кг

Маса картоплі:

2. М=0,2м+900
3.  0,8м=900
4. 

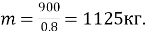
ВІДПОВІДЬ: Картоплі потрібно

 

ЗАДАЧА №19

 

На одну порцію чаю потрібно 200гр води необхідно 20гр цукру ціна якого 0,44коп

По ціні 8і 1,5 гр чаю по ціні 50 коп. Для приготування 1л води необхідно затратити 0,1квт/час електроенергії  по ціні 25 квт/ч. Вирахувати собівартість 1 стакану чаю.

 

РОЗВЯЗАННЯ:

1. Ціна цукру 8*0,02=0,16 коп
2. Ціна чаю 50 коп
3. Ціна електроенергії

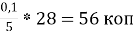
Всього: 16+50+1=67коп

ВІДПОВІДЬ: На чай потрібно затратити 67копійок