Призма, види призм. Паралелепіпеди

Лекція: Призма, види призм. Паралелепіпеди

План

1. Поняття призми.  Види призм.
2. Площі бічної та повної поверхонь призми.
3. Поняття перерізу многогранника. Перерізи призми.
4. Паралелепіпед та його види. Властивості паралелепіпеда. Прямокутний паралелепіпед.
5. Площі бічної та повної поверхонь прямокутного паралелепіпеда та куба.

Література

1.     Геометрія: 11 кл.: підруч. для загальноосвіт. навч. закл.: академ. рівень, проф. рівень / Г.П. Бевз, В.Г. Бевз, Н.Г. Владімірова, В.М. Владіміров. [Електронний ресурс]  – К.: Генеза, 2011. – с. 136 –151.
2.     Математика. Комплексна підготовка до ЗНО і ДПА / Уклад. А.М. Капіносов [та ін.]. – Тернопіль: Підручники і посібники 2017. –     с. 418-428.

1. Поняття призми. Види призми

Одним  з  найпростіших  многогранників є призма.

Призмою називають многогранник, у якого дві грані між собою рівні і лежать у паралельних площинах (їх називають основами призми), а всі інші грані – паралелограми ( їх називають бічними гранями призми).

Мал. 1 – Призма

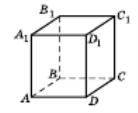
На мал. 1 зображено призму, основами якої є чотирикутники ABCD і  A₁B₁C₁D₁.  Призму  прийнято  називати  за  назвою  її  основ,  наприклад, на  мал. 1  зображено  призму ABCDA₁B₁C₁D₁.  Сторони  бічних  граней призми, які не належать основам, називають бічними ребрами призми.

На  мал. 1  паралелограми AA₁D₁D, ABB₁A₁, BB₁C₁C і CC₁D₁D – бічні  грані  призми;  AA₁,  BB₁,  CC₁ і DD₁ – бічні ребра призми. Зрозуміло, що всі бічні ребра призми паралельні і рівні між собою.

Призму називають п-кутною, якщо її основою є п-кутник. (На мал. 1 зображено чотирикутну призму).

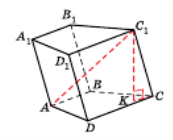
Перпендикуляр, проведений з деякої точки однієї основи  до  площини  іншої  основи,  називають  висотою призми. (На мал. 1 відрізок C₁K – висота призми).

Відрізок, що сполучає дві вершини призми, які не лежать в одній грані, називають діагоналлю призми. (На мал. 1 відрізок C₁A – діагональ призми).

Призму називають прямою, якщо її бічні ребра перпендикулярні  до  її  основ,  в  іншому  випадку  призму називають похилою.

На мал. 1 зображено похилу чотирикутну призму, а на мал. 2 – пряму трикутну призму. Зрозуміло, що бічні грані прямої призми – прямокутники, а висота прямої призми дорівнює її бічному ребру.

Пряму призму називають правильною, якщо її основою є правильний многокутник. На мал. 3 зображено правильну чотирикутну призму. У правильній призмі всі бічні грані – рівні прямокутники.

2. Площі бічної та повної поверхонь призми

Площею  повної  поверхні  призми  називають  суму площ усіх її граней, а площею бічної поверхні призми – суму площ її бічних граней.

Площу повної поверхні призми S_повн можна записати через площі її бічної поверхні S_біч і її основи S_осн формулою:

S_повн = S_біч + 2S_осн.

Т е о р е м а   (про  площу  бічної  поверхні  прямої  призми): Площа бічної поверхні прямої призми дорівнює добутку периметра основи P на висоту призми, тобто на довжину її бічного ребра l:

S_біч = Pl.

3. Поняття перерізу многогранника. Перерізи призми

Умови багатьох геометричних задач використовують  поняття  перерізу

многогранника.  Тож  для  розв’язування таких задач треба навчитися будувати переріз многогранника  площиною. 

Січною  площиною  многогранника  називають будь-яку площину, по обидва боки якої є точки даного многогранника. Січна площина перетинає грані многогранника по відрізках. Многокутник, сторонами якого є ці відрізки, називають перерізом многогранника.

Мал. 4 – Переріз многогранника

Наприклад, на мал. 4 чотирикутник KLMN є перерізом трикутної піраміди QABC.

Січна  площина може  бути  задана  одним  із  відомих способів:  трьома  точками,  що не  лежать  на  одній  прямій,  або  прямою і точкою, що їй не належить, або двома прямими, що перетинаються.

Перерізи призми

Переріз  призми,  який  проходить через  два  бічних  ребра,  що  не  лежать в одній грані, називають діагональним перерізом призми.

Мал. 5 – Діагональний переріз прямої призми

На мал. 5  чотирикутник АА₁C₁C – діагональний переріз прямої призми АВСDА₁В₁C₁D₁. Цей переріз є прямокутником, одна зі сторін якого – діагональ основи АC, а інша – бічне ребро АА₁. У похилій призмі діагональним перерізом є паралелограм.

Розглянемо переріз похилої призми площиною, яка проходить  через  точку  M  бічного  ребра  AA₁  перпендикулярно  до цього  ребра  та  перетинає  кожне  з  інших  бічних  ребер  цієї призми (Мал. 6).

Мал. 6 – Перпендикулярний переріз призми

Зрозуміло, що площина перерізу буде перпендикулярною до всіх інших бічних ребер призми. Такий переріз називають перпендикулярним перерізом призми. На мал. 6  чотирикутник  MNLK  – перпендикулярний переріз.

Перпендикулярний  переріз  прийнято  розглядати  лише  в  похилій  призмі, оскільки, очевидно, що у прямій призмі він дорівнює многокутнику, що є основою призми.

4.              Паралелепіпед та його види. Властивості паралелепіпеда. Прямокутний паралелепіпед

У шкільному курсі математики ти познайомився з прямокутним паралелепіпедом і кубом. Обидва ці тіла є видами паралелепіпеда. Розглянемо паралелепіпед детальніше.

Паралелепіпед - це призма, основою якої є паралелограм.

У паралелепіпеда всі грані – паралелограми.

Оскільки  паралелепіпед  є  призмою,  то  всі  властивості призми справджуються і для паралелепіпеда.

Паралелепіпед, бічні ребра якого перпендикулярні до площини основи, називають прямим паралелепіпедом. Його бічні грані – прямокутники. На мал.7 зображено прямий паралелепіпед.

 Якщо  бічні  ребра  паралелепіпеда  не  перпендикулярні  до площини основи, його називають похилим паралелепіпедом. На мал. 8 зображено похилий паралелепіпед.

Грані паралелепіпеда, які не мають спільних вершин, називають  протилежними  гранями.  На  мал. 8  протилежними є грані ABCD і A₁B₁C₁D₁, ABB₁A₁ і CDD₁C₁, AA₁D₁D і BB₁C₁C.
Розглянемо властивості паралелепіпеда:

Теорема (Властивість протилежних граней паралелепіпеда): протилежні  грані  паралелепіпеда  паралельні і рівні.

Теорема (Властивість діагоналей паралелепіпеда): діагоналі паралелепіпеда перетинаються і точкою перетину діляться навпіл (мал. 9).

Мал. 9

Прямокутним паралелепіпедом називають  прямий  паралелепіпед,

основою якого є прямокутник.

Зауважимо,  що  всі  грані  прямокутного  паралелепіпеда  є прямокутниками, а всі двогранні кути – прямими.

Довжини  трьох  ребер  прямокутного  паралелепіпеда,  які виходять з однієї вершини, називають вимірами (або лінійними вимірами) прямокутного паралелепіпеда.

На мал. 10 AB = a, AD = b, AA₁ = c – виміри прямокутного  паралелепіпеда. Зрозуміло, що даний прямокутний паралелепіпед має чотири ребра завдовжки a, чотири – завдовжки b і чотири – завдовжки c.

Мал. 10 – Прямокутний паралелепіпед

Виміри  прямокутного паралелепіпеда зазвичай називають  довжиною,  шириною  і  висотою, ці  самі  терміни  використовують  і  на практиці. Наприклад, так ми називаємо виміри кімнати, коробки, що має форму прямокутного паралелепіпеда, тощо.

Теорема (Про  довжину  діагоналі  прямокутного паралелепіпеда):  Квадрат  діагоналі  прямокутного  паралелепіпеда дорівнює сумі квадратів трьох його вимірів:

d²=a²+b²+c².

Наслідок: Усі  чотири  діагоналі  прямокутного  паралелепіпеда рівні.

Прямокутний паралелепіпед, усі три виміри якого рівні, називають кубом. Усі грані куба – рівні між собою квадрати.

5.              Площі бічної та повної поверхонь прямокутного паралелепіпеда та куба

Прямокутний паралелепіпед

Бічна поверхня:

Повна поверхня:

Куб

Бічна поверхня:

Повна поверхня:

Домашнє завдання

1. Написати конспект та вивчити теоретичний матеріал.
2. Навести приклади предметів із повсякденного життя, які мають форму прямої та похилої призми, прямокутного паралелепіпеда та куба.