Проект з геометрії на тему "Золота теорема геометрії"

 

                         

Назва проекту: «Золота теорема геометрії»

Керівник проекту: Горбаченко Тетяна Олександрівна

Місце роботи: Миронівська ЗШ  І-ІІ ступенів Світловодського р-ну

Предмет: Геометрія

Вік учнів: 13 - 14 років

Склад учасників проекту: учні, вчитель математики та історії, бібліотекар

Тип проекту: Пізнавальний, дослідницький, творчий

За кількістю учасників: груповий

За тривалістю підготовки: короткотривалий ( два тижні)

 

Педагогічний девіз проекту:

   «Немає абстрактного учня… Мистецтво й майстерність навчання і виховання полягає в тому, щоб розкривши сили й можливості кожної дитини дати відчути їй радість успіху в розумовій праці»                                    

 

                                                              В. О. Сухомлинський

Задачі проекту: 

• розширити знання учнів з геометрії про прямокутний трикутник та теорему  Піфагора;
• познайомити учнів з різними доведеннями теореми Піфагора;
• усвідомити важливість даної теореми.

Тематичні питання:

1. Хто такий Піфагор? Які відкриття в математиці зробив він та його учні?
2. Чому теорема про сторони трикутника носить ім’я Піфагора й чи відповідає це дійсності?
3. Які існують способи доведення теореми Піфагора?
4. Де і як можна її використовувати?
5.  Чи актуальна теорема Піфагора в наш час?

 

 

Мета:

• познайомити учнів зі змістом та різними доведеннями теореми Піфагора;  формувати вміння застосовувати її до розв’язування задач;

 

• узагальнити знання про прямокутний трикутник; розширити коло геометричних завдань, що вирішуються учнями;

 

• ознайомити учнів з основними етапами життя і діяльності Піфагора;

 

• реалізувати міжпредметні зв’язки геометрії з алгеброю, географією, історією, біологією, літературою;

 

• розвивати дослідницькі та комунікативні здібності дітей, прищеплювати навички співпраці з іншими людьми, розвивати вміння, збирати інформацію та вмотивовано викладати висновки.

Необхідне устаткування: комп’ютер, принтер, цифровий  фотоапарат.

Додаткове приладдя та матеріали: Кольоровий папір, фломастери, папір, учнівські зошити.

 

      Анотація

   Під час роботи над проектом, учні не тільки навчаться збирати первинну інформацію, вони познайомляться із теоремою Піфагора, зможуть її доводити і застосовувати під час розв’язання задач. Удосконалять та поглиблять свої знання із даної теми. Виявлять зв'язок математики з мистецтвом, музикою, географією, астрономією. Відкриють для себе багато нового, цікавого захопляться історією математики. Навчаться захищати свій проект перед однокласниками, критично мислити, розмірковувати, робити висновки, приймати самостійні рішення,  діяти в команді спілкуючись і співпрацюючи.

Опис проекту:

    Проект пропонується для реалізації з учнями 8 класу під час вивчення теми «Теорема Піфагора». Даний проект об’єднує історію, математику, географію, літературу та інформатику. У ході практичної діяльності учні повинні дослідити біографію відомого вченого, розглянути його знаменну теорему, способи її доведення і застосування для розв’язання задач. Також під час роботи над проектом учні повинні дослідити теорему Піфагора, використовуючи деякі способи її доведення. Працюючи над проектом, учні розширюють і поглиблюють свої знання з геометрії. Клас поділено на п'ять груп: «Історикознавці», «Теоретики», «Літературознавці», «Практики» та «Філософи».

 

Очікувані результати: створення комп'ютерної презентації.

Етапи роботи над проектом:

1. Об’єднання учнів у групи за інтересами;
2. Розподіл обов’язків;
3. Пошук інформації; оформлення матеріалів;
4. Пошук відповідей на тематичні питання, узагальнення результатів, досліджень і створення звіту у вигляді презентації.

Діяльність учасників та етапи проведення проекту.

Підготовчий: 

Учитель коментує тему і мету проекту. Мотивує діяльність учнів. Обговорює цілі і головні питання проекту.

Планування:

Учні об’єднуються в групи: історикознавці ( вивчають біографію, результати оформляють у вигляді публікацій); теоретики (розшукують різні способи доведення теореми Піфагора, результати оформляють у вигляді публікацій ); практики (збирають ісоричні завдання, у вирішенні яких застосовується теорема Піфагора, результати оформляють у вигляді публікацій), літературознавці (вивчають відображення теореми Піфагора в літературі, результати оформляють у вигляді публікацій ), філософи (вивчають досягнення Піфагора, його філософські вислови, їх зв'язок з сучасністю, результати оформляють у вигляді публікацій). Учні розприділяють обов’язки.

Дослідницький:

Відбувається збір інформації по теоремі Піфагора, пошук відповідей на основні питання з подальшим обговоренням, аналізом та корекцією. Кожна група обирає питання та відповідає на них.

Презентативний:

                     Звіт про проведену роботу (проведення уроку-  

                     захисту проекту на тему «Золота теорема 

                     геометрії»).

Ком'пютерна презентація по даному проекту.

 

Результати проведеної роботи були представлені на уроці.

Тема уроку: Теорема Піфагора.

 

Мета уроку: Познайомити учнів зі змістом та різними

                        доведеннями теореми Піфагора; формувати вміння

                        застосовувати теорему Піфагора до розв'язування

                        задач; узагальнити знання про прямокутний

                        трикутник; розширити коло геометричних завдань,

                        що вирішуються учнями; ознайомити учнів з

                        основними етапами життя і діяльності Піфагора;

                        реалізувати міжпредметні зв’язки геометрії з

                        алгеброю, географією, історією, біологією,

                        літературою; розвивати дослідницькі та

                        комунікативні здібності дітей, прищеплювати

                        навички співпраці з іншими людьми, розвивати

                        вміння збирати інформацію та вмотивовано

                        викладати висновки.

 

Обладнання: ілюстрації із зображенням Піфагора та сцен із його

                         життя, пентагами персня піфагорійців; плакати, на

                         яких написано найвідоміші філософські вислови

                         Піфагора; комп'ютер для перегляду презентації.

 

Тип уроку: Засвоєння нових знань.

 

                                              Не роби ніколи того, що не знаєш.

Але вчись усьму, що потрібно знати,

І тоді будеш вести спокійне життя.

                                                                                       Піфагор

 

ХІД  УРОКУ

 

І. Організаційна частина.

   Вступне слово вчителя:

   Прямокутний трикутник – одна з перших геометричних фігур, про властивості якої людство дізналось ще в давнину. Задачі про  трикутник знаходять у давньоєгипетських папірусах, старовинних індійських книгах. У папірусі Ахмеса згадується про властивості рівнобедреного та прямокутного трикутників, данві вавілоніни 4000 років тому вже знали про кути при основі рівнобедреного трикутника. Ознаки рівності трикутника були сформовані Евдемом Родоським та Фалесом Мілетським. У Давній Греції в іонійській математичній школі (заснована а VI столітті до нашої ери Фалесом) та у школі Піфагора знали види й властивості трикутників. Систематизував ці відомості Евклід у першому трактаті з геометрії «Началах».

   Чому ж трикутник цікавив людей з давніх часів? Жорсткість трикутників використовували під час будівництва й конструювання.

 

ІІ. Актуалізація опорних знань учнів.

    Технологія «Мікрофон»:

   Учень дає відповідь на одне запитання та передає мікрофон наступному учневі.

1. Трикутник, у якого є прямий кут… (прямокутний).
2. Сторона прямокутного трикутника, що лежить проти прямого кута… (гіпотенуза).
3. Перпендикуляр, проведений з вершини трикутника на протилежну сторону або на її продовження… (висота).
4. Відрізок, що сполучає основу перпендикуляра з основою похилої… (проекція).
5. Які проеції мають рівні похилі? (рівні).
6. Яка проекція більшої похилої? (більша).
7. Сформулюйте основну нерівність трикутника… (у будь-якому трикутнику кожна сторона менша за суму двох інших сторін).

 

ІІІ. Мотивація навчальної діяльності.

   Найпопулярнішою з усіх теорем планіметрії є теорема Піфагора. Причинами такої популярності є простота, краса і значення.

   Про теорему Піфагора так сказав німецький вчений Йоганн Кеплер: «У геометрії є два скарби: перший – теорема Піфагора, другий – золотий поділ. Перший можна порівняти з мірою золота, другий – із коштовним каменем».  

   Цю теорему називають вічною. Їй понад 2 тисячі років. В епоху Середньовіччя її називали «ослячим містком», тому що довести її було важко для тогочасних науковців. Тож спробуємо і ми перейти цей «ослячий місток».

 

IV. Повідомлення учнів.

  Разом навчатися не тільки  

    легше й цікавіше, але й 

      значно ефективніше.

                        Є. С. Полат

   «Історикознавці» (1-а група) про життя Піфагора

 

   Легенда про народження

    Піфагор жив у 6 столітті до нашої ери. Він  народився у Греції, на острові Самос у сім’ї  золотих справ майстра Мнесарха.  За легендою оракул пророчив йому та його дружині Парфенісі народження сина, який буде славитися віками своєю мудрістю,  справами та красою. Пророцтво збулося, і тоді Парфеніса приймає ім’я Піфіада, на  честь Аполлона Піфійського, а сина називає Піфагором, на честь пророцтва Піфії. У легенді нічого не сказано про рік народження Піфагора, історичні дослідження датують його появу на світ приблизно 580 роком до нашої ери.

   Дитячі та юнацькі роки

   Можливості дати сину гарну освіту та виховання у Мнесарха були. Як і будь-який батько, Мнесарх мріяв, що син буде продовжувати його справу – ремесло золотих справ майстра. Життя вирішило інакше. Майбутній математик та філософ вже в дитинстві виявив велику здатність до наук. У свого першого вчителя Гермодамаса Піфагор отримав знання основ музики та живопису. Для покращення пам’яті Гермодамас примушував його вчити пісні з «Іліади» та «Одіссеї». Перший вчитель навчив Піфагора любити природу та вивчати її таємниці.

   Пройшло кілька років, і за порадою свого вчителя Піфагор вирішує продовжити навчання в Єгипті, у жерців. Потрапити до Єгипту у той час було дуже важко, тому що країну практично закрили для греків. За допомогою вчителя Піфагору вдається залишити острів Самос. Але до Єгипту далеко, і Піфагор поки що живе на острові Лесбос. Там відбувається знайомство Піфагора з філософом Ферекідом – другом Фалеса. У Ферекіда Піфагор навчається астрології, таємницям чисел, медицині та іншим обов’язковим, на той час, наукам. Піфагор прожив на Лесбосі кілька років. Звідти шлях Піфагора лежить у Мілет до відомого Фалеса, засновника першої в історії філософської школи.

Навчання Піфагора в Єгипті сприяє тому, що він стає одним із найбільш освічених людей свого часу. Волею долі 12 років прожив Піфагор у Вавилоні, де прилучився до східної астрології та містики. І тільки в 60 років Піфагору вдалося повернутися на Батьківщину.

Піфагорійська школа

   Після повернення додому Піфагор переселився  до Південної Італії, яку  тоді називали великою  Грецією. Тут, на острові  Сицилія в Кротоні, у нього  народжується власна  філософська школа.

   Це був одночасно і релігійний союз, і політичний клуб, і наукове товариство. Учні цієї школи зобов’язувались вести так званий піфагорійський спосіб життя. Статут піфагорійського союзу був дуже суворим. Кожний, хто вступав до нього, відмовлявся від особистої власності на користь союзу, зобов’язувався не проливати крові, не вживати м’ясної їжі, берегти таємницю вчення свого вчителя. Членам школи заборонялося навчати інших за винагороду. Всі учні Піфагора і він сам були працелюбні. Досконало володіючи методами єгипетських жерців, Піфагор «очищував душі своїх слухачів, виганяв вади з серця та наповнював уми світлою правдою». В «Золотих віршах» Піфагор показав ті моральні правила, суворе виконання яких призводить до ідеалу. Ось декілька з них:

        1) Роби лише те, що в результаті не засмутить тебе і не примусить каятися.

 2) Не роби ніколи того, чого ти не знаєш. Але навчися усього, що варто знати, і тоді будеш вести спокійне життя.

 3) Не зневажай здоров’ям свого тіла. Доставляй йому вчасно їжу і питво, і вправи, без яких воно бідує.

 4) Привчайся жити просто, без розкоші.

 5) Не закривай очей, коли хочеться спати, не проаналізувавши успіх своїх вчинків за минулий день.

 6) Не порушуй справедливість.

 7) Не сідай на подушку (тобто не зупиняйся на досягнутому).

 8) Не гризи свого серця (тобто не піддавайся меланхолії).

 9) Не поправляй вогню мечем (тобто не дратуй тих, хто і без того в гніві).

 10) Не приймай під свій дах балакунів і легковажних людей.

 11) Усе впорядковується відповідно до чисел.

 12) Лише не благородна людина здатна в очі хвалити, а поза очі злословити.

 13) Тимчасова невдача краще тимчасової удачі.

 14) Твори велике, не обіцяючи великого.

 15) Живи з людьми так, щоб твої друзі не стали недругами, а недруги стали друзями.

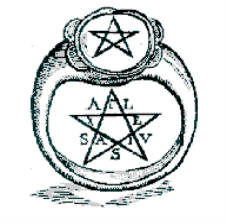
   На персні Піфагора було викарбувано

 такий девіз: «Тимчасова невдача краща

тимчасової удачі».

   У якості символа піфагорійці вибрали пентаграму – п’ятикутну зірку. Це символ здоров’я і досконалості, опізнавальний знак піфагорійців.

 

 

 

 

 

 

Філософське вчення Піфагора

 

   Піфагор навчав медицині,принципам політичної діяльності,

астрономії, математиці, музиці, етиці.З його школи вийшли відомі

політичні та державні діячі,історики, математики та астрономи.

Це був не лише вчитель, але й дослідник.Дослідниками ставали і його учні.

   Щоб зрозуміти роль піфагорійської школи в розвитку математичної науки, слід охарактеризувати її філософське вчення. Піфагорійці вважали, що в природі існують дух і матерія, і надавали числам містичного значення. Вони гадали, що речі – це відображення чисел, число – це закон і зв'язок світу, це сила, яка керує богами і смертними. Тому природу і всевладну силу числа можна бачити не тільки в ділах божих, а й в усіх людських заняттях – мистецтві, ремеслах, музиці. Піфагор відкрив важливий закон музики, за яким висота тону струни обернено пропорційна до її довжини. Він визначив також, що коли довжини струн відносяться як 6:4:3, то при одночасному звучанні вони дають приємний гармонійний акорд; якщо ж ці числа змінити, то звукова гармонія порушується. Піфагор поширив закон гармонії на інші явища природи, узагальнив його. Виходячи із своїх ідей, піфагорійці проводили дослідницьку роботу в математиці. Вони комбінували числа і, надаючи їм містичного значення, ділили їх на числа добрі –  непарні числа; злі – парні числа: досконалі – кожне з яких дорівнює сумі своїх дільників (якщо з числа-дільників виключити саме число). Наприклад, досконалим числом є 6, бо сума його дільників 1, 2, 3 дорівнює шести. Числа дружні – це числа, з яких одне дорівнює сумі дільників другого, але також без цього самого числа. Були в них числа пірамідальні, многокутні і т. д. Зокрема, прямокутним називали ціле число, що дорівнює добутку двох інших цілих чисел.

    Піфагор розвивав теорію музики й акустики,створив відому «піфагорійську гаму».

   У школі Піфагора вперше був виказаний здогад щодо кулястості Землі.

   Піфагор був переможцем на 58-х Олімпійських іграх, які проходили в 548 році до нашої ери, а потім перемагав ще на декількох Олімпіадах.

    Відомо, що Піфагор  був міцним юнаком з товстою шиєю та коротким носом,  малим на зріст, тому судді однієї з перших олімпіад не хотіли допускати його до змагань. Але він пробився і «побився»  зі своїм супротивником та ще і переміг. Ось чому серед знаменитих олімпійських чемпіонів він довго залишиться найвідомішим. Ось чому люди пам’ятають його більше, як дві з половиною тисячі років, тому що йому випало щастя перемогти не тільки супротивників, а й перемогти час.

 

V. Вивчення нового матеріалу.

   1. Формулювання теореми за Піфагором: сума площ квадратів, побудованих на катетах прямокутного трикутника, дорівнює площі квадрата, побудованого на гіпотенузі.

    

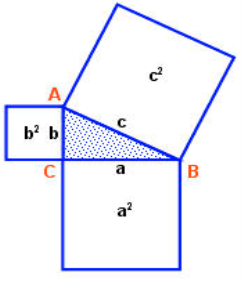
 a² + b² = c²

 

 

 

 

 

 

   2. Сучасне формулювання теореми Піфагора (учні записують у зошит): у прямокутному трикутнику сума квадратів катетів дорівнює квадрату гіпотенузи.

 a² + b² = c² А 

 

 с b

  

 В a С

   3. Історична довідка про теорему Піфагора.

Учитель: Про теорему знали давно, що 2000 років тому. Її використовували у Стародавньому Єгипті для трикутника зі сторонами 3, 4 і 5 відрізків (перевірте, чи справджується теорема для таких сторін прямокутного трикутника).

   На сьогодні існує близько 300 доведень цієї теореми, і мабуть, Піфагор був не першим, хто довів її. Проте завдяки йому ця теорема перейшла з практичної галузі у науковву.

   Інша назва теореми «Гекатомба», що в перекладі означає сто биків, які нібито приніс Піфагор в жертву богам в честь доведення цієї теореми.

   Доведемо і ми цю теорему.

 

«Теоретики» (2-а група) з різними доведеннями теореми Піфагора

  «Немає більш надійного способу доказу, ніж спосіб   

       математиків, які підтверджують виведені формули прикладами й перевіркою на практиці»                                                                          

                   М.В. Ломоносов

 

  Теорема Піфагора має народні назви. 

 У Франції і деяких областях Німеччини в середні віки її називали „ослиним мостом”, тому що доведення теореми було величезною перешкодою, так званим мостом, перейти який могли тільки розумні учні.

 У математиків арабського Сходу ця теорема одержала назву „теореми нареченої”. Справа в тому, що в деяких списках „Начал” Евкліда ця теорема називалася „теоремою німфи” за подібність креслення з метеликом, що грецькою звався німфою. Але цим словом греки називали деяких богинь, а також наречених. При перекладі арабський перекладач, не звернувши уваги на креслення, переклав слово „німфа” як „наречена”, а не „метелик”.

 А відома всім школярам назва „Піфагорові штани” виникла через схожість креслення до Евклідового доведення теореми зі штаньми.

   Говорять, що теорема Піфагора не зовсім справедливо названа на його честь. Ця теорема була відома за 1500 років до Піфагора. Існують великі сумніви, що саме йому належить доведення теореми. Але не зважаючи на це, всі переконані, що Піфагор та його учні зробили так багато для розвитку математики, що ця історична несправедливість не вражає.

1-й спосіб доведення теореми Піфагора.

    Індійський математик Бхаскара ІІ подав його у формі креслення, під яким було написано лише одне слово „Дивись!”.

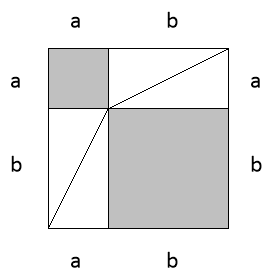Спосіб доведення без слів «Дивись!» він прийшов із давньої Індії

 

 

 

 

 

 

 

Показано два рівні квадрати із сторонами а + в і написано одне слово «дивись». В квадраті із Істріною а + в намальовано чотири рівних прямокутних трикутники з катетами а і в  на першому рисунку фігура вільна від трикутників, складається із двох квадратів із сторонами а і в, відповідно їх площа дорівнює а² + в². На наступному

рисунку  фігура вільна від трикутників – це квадрат із стороною с, його площа дорівнює с². Отже , оскільки квадрати рівні, то

с² = а² +в², що і складає твердження теореми  Піфагора.

 

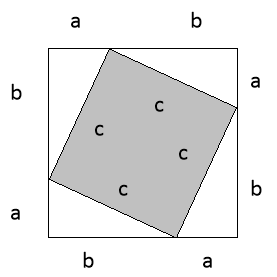
2-й спосіб доведення теореми Піфагора.

Доведення Платона, його можна зрозуміти дивлячись на рисунок.

 

 

 

 

 

 

 

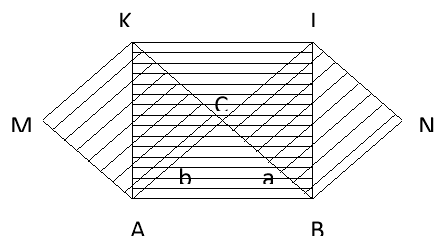
3-й спосіб доведення теореми Піфагора.

      Цей метод доведення побудований на розрізанні квадратів, побудованих на катетах, і складанні одержаних частин на квадраті, 

         побудованому на гіпотенузі.

 

 4-й спосіб доведення теореми Піфагора. 

 

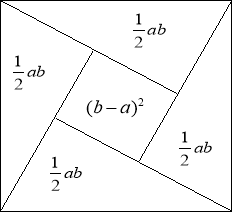Алгебраїчний спосіб. Це доведення великого індійського математика Бхаскари. Воно також супроводжувалось словом

«дивись!».

На даному рисунку

С²= 4 ∙ ав +(в – а)²,

              2

С² = 2ав +в² – 2ав + а²,

С² = в² + а².

 

 

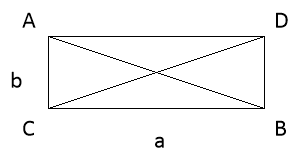5-й спосіб доведення теореми Піфагора.

 

   Доповнено прямокутний трикутник до 

      прямокутника і скористаємось  теоремою про суму  квадратів 

           діагоналей.

 2(а² +в²) = 2с², або а² + в² = с²

6-й спосіб доведення теореми Піфагора.

  До кола із центром у точці С проведемо дотичну АВ і січну АМ, яка проходить

 

 

 

 

 

 

 

 

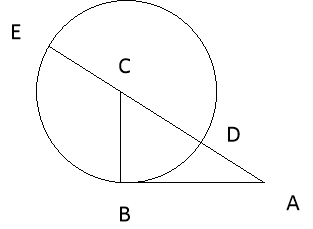
 через центр кола С. За теоремою про січну і дотичну АВ² = АД².  АМ. (1) Оскільки    АС = СД + АД, АМ = АС + СМ = АС + СВ, то АД = АС – СД = АС – СВ. Підставимо ці значення в формулу (1) отримаємо АВ² = (АС – СВ)(АС + СВ), або АВ² = АС² – СВ²,

АВ² +СВ² = АС², що і потрібно було довести.

 

VI. Закріплення нових знань.

 

   Розв’язування усних вправ за готовими малюнками:

 

  1)       

             а = 8 см               с = 17 см

 

 

                                            b = ? см

 

2) 3)

 

b = 4 м  с = ? м                          с = 10 дм                  b = 6 дм

 

 

 

 а = 3 м а = ? дм

 а = 3 м

 

   Учитель: Тепер, перейшовши «ослячий Місток», приступимо до розв’язання складніших задач.

 

 «Практики» (3-я група) з історичними та старовинними задачами, у яких застосовувалась теорема Піфагора.

                                                                         Ці задачі не прості,

                                                                     Застосуєш їх в житті.

                                                                     Щоб їх добре розв’язати,

                                                                 Геометрію потрібно знати.

 

 

 

 

1. Задача індійського математика

ХІІ століття Бхаскари:

                        

 

 

 

 

 

 

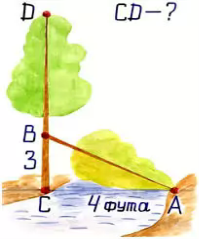
На березі ріки росла самотня тополя.

Раптом налетівші вітри зламали її стовбур.

Бідна тополя впала, утворивши кут між стовбуром

і поверхнею води річки. Запамятай тепер,

що в цьому місці річка у чотири лише фути була

шириною. Верхівка ж зламалась, залишивши

всього  три фути від усього стовбура.

Прошу тебе, скоріше тепер мені скажи:

яка висота тополі?

 

 

 

 

 

 

 

 

             2.Задача з підручника «Арифметика»

                            Леонтія Магницького:

 

 

 

 

 

 

 

 

 

 

 

 

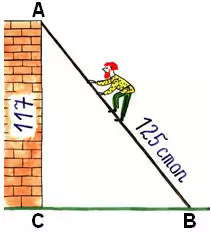
          Сталося деякій людині до стіни сходи прибрати,

                       стіни ж тієї висота була 117 стоп.

                  І узяв він драбину завдовжки 125 стоп.

                    І дізнатися він хоче, на скільки стоп

                             цю драбину нижнім кінцем

                              від стіни відставити треба.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

               

                    3. Задача «Стрибок мавпочки»:

 

 

 

 

 

 

 

 

 

На дереві сиділо дві мавпочки:

                                одна на самій верхівці дерева,

                            інша – на висоті 10 ліктів від землі.

Другій мавпочці захотілося напитися води

з джерела, що знаходилось на відстані

40 ліктів від дерева.

Вона злізла з дерева і пострибала до води.

У той самий час перша зістрибнула з дерева

 І потрапила до цього ж джерела.

Обидві мавпочки подолали однакову відстань.

Визначте, з якої висоти зістрибнула

перша мавпочка.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4.Задача із китайської

«Математики в дев'яти книгах»:

 

 

 

 

 

 

 

 

 

 

 

Маємо водойму зі стороною в 1 чжан = 1 чи.

В центрі водойми росте очеретина,

яка виступає над водою на 1 чи.

Якщо потягнути очеретину до берега,

то вона якраз доторкнеться до нього.

Запитання: яка глибина водойми і

яка довжина очеретини?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                               

5.Задача «Зламаний бамбук»:

 

 

 

 

 

 

 

 

 

 

 

Бамбук, що має 40 ліктів у висоту,

зламав вітер. Його верхівка

торкнулася землі за 20 ліктів

від основи стовбура.

Скажи, о мудрий математику,

на якій висоті від землі

було зламано бамбук?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

  

 

 

 

                           6.  Задача «Дві вежі»:

 

 

 

 

 

 

 

 

 

 

                        Дві вежі, висотою 30 і 40 футів,

                         розташовані одна від одної на

                           відстані 50 футів. Між ними

                                  знаходиться фонтан,

                         до якого одночасно з верхівок

                           веж з однаковою швидкістю

                        вилетіли два голуби. Визначте,

                               яка відстань від фонтана

                       до кожної з двох веж, якщо голуби

                          долетіли до нього одночасно?

 

 

 

 

 

 

 

 

 

 

 

 

 

                  7.Задача «Мурашка на піраміді»:

 

 

 

 

 

 

На вершину єгипетської піраміди

найкоротшим шляхом

повзе мурашка із швидкістю 2 м/хв.

Скільки часу необхідно мурашці,

щоб дістатися до вершини піраміди,

якщо довжина її основи 232 м,

 а кут між бічним ребром і стороною 58^○?

 

 

 

 

 

 

    Інтерактивна вправа «Акваріум»

   Учитель пропонує розв’язати задачі 4 та 5 і показує малюнок до них на плакаті. Учні 3-ї групи («Практики») сідають у центрі класу. Ця група спочатку читає вголос 4 задачу, а потім обговорює її. За 3-5 хвилин вони повинні знайти спільне розв’язання. Учні, які знаходяться у зовнішньому колі, слухають не втручаючись у хід обговорення. Після розв’язання задачі місце в «акваріумі» займає інша 2-а група («Теоретики») і обговорює розв’язання задачі 5.

 

   VII. Важливість теореми Піфагора.

Учитель. Теорема Піфагора – це, напевно, єдина теорема, яку пам’ятають усі учні. Ті, що добре вчилися, знають формулювання, доведення, а інші – назву. Та, напевно, кожен пам’ятає вислів: «Піфагорові штанці рівні є у всі кінці».

 

«Літературознавці» (4-а група) про оспівування теореми Піфагора в легендах та віршах.

                                                    

       Математика і поезія – це… вираз 

            тієї самої сили уяви, тільки в  

 першому  разі уява звернена до голови,

                  а в другому – до серця.                                            

                                                         Т. Хілл

   Німецький поет ХІХ століття Адельберт фон Шаміссо теоремі присвятив сонет:

Як Істину відкрив – сіять їй вічно,

Вона нам – найнадійніша опора:

Так в древній теоремі Піфагора

Й донині бездоганно все й логічно.

Богам дарунок щедрий був й незвичний

За те, що осяйнуло його вчора:

Чекало сто биків розправа скора, -

В віках луна їх рев жертовний звично.

З тих пір бики жахаються й тремтять,

Як істину нову являє прогрес,

Безсилі їй на перешкоді стать,

Й зливається їх рев в жалобний хор, -

Знов древній страх той в генах їх воскрес,

Що в них колись вселив ще Піфагор.

 

  Німецький поет Г. Вебер у своєму творі писав:

Ввів інший поет вже цю тему

В свій вірш, - але як мені буть?

Прадавню одну теорему

Не можу я забуть.

Стояв там трикутник, як ментор,

Й один кут прямий в йому був,

І саме ось цим елементом

Він славу й визнання здобув.

Вродливиці гіпотенузі,

Що стрімко здіймалася ввись,

Два  катети, вірнії друзі,

В любові до смерті клялись.

Та їхні обійми їй тісні,

Тож пісню співає вона,

Й геометрам всім у цій пісні

Втіх більше, а ніж від вина.

Хто зовсім ще глузду не втратив,

Не може забути про це,

Що сума для а й в квадратів

Квадратові рівна для с!

Ця пісня й холодній медузі

Тепла і жаги додала.

Вже лиш за це гіпотенузі

Й двом катетам честь і хвала!

 

   Є і польська епіграма Леха Конопінського про теорему Піфагора:

В любовних трикутниках найбільш рогаті

Ті, що є ослами у квадраті.

 

   Тема теореми Піфагора звучить і у таких віршах:

Жил на свете математик Пифагор,

И о нем пойдет сегодня разговор.

Сочинял он теоремы, и не раз,

Удивить хотел, как видно, нас.

Только не надо переживать.

По теореме легко считать.

Гипотенузу в квадрат возведешь,

Квадратов катетов сумму найдешь.

Шил себе штаны однажды геометр,

Но не мог найти любимый метр.

Вот тогда он теорему сочинил,

Ту, которой мир весь покорил.

Только не надо переживать.

При чём здесь брюки, ты хочешь знать?

Когда докажем теорему мы,

Рисунок будет похож на штаны.

Сшил штаны по чертежам своим мудрец.

В них он покорил немало девичьих сердец.

Были на все стороны равны, -

Сейчас про это точно знаем мы.

                                                                                 А. Новиков

В дни глубокой старины

Жил чудак одной страны,

На загадки всего света

 Он искал свои ответы.

Полумаг и полубог,

И немножечко пророк,

Да с умом-то философским,

Это – Пифагор Самосский.

Про ученье Пифагора

 В мире было много спора,

Где легенда, а где быль? –

Занесла дороги пыль.

Кварты, квинты и октавы,

Пифагоровы составы.

Акустический пробел

Завершить на слух хотел.

Но любимою была

Геометрии страна.

Треугольник да квадрат

Он вертел на дню стократ.

Как-то раз, поняв, в чём дело,

Пифагор воскликнул смело:

«В треугольнике прямом

Есть зависимость сторон.

Братья-катеты углом,

С ними можно строить дом.

Их сестра гипотенуза

Сохраняет прочно узы.

«А» квадрат плюс «В» квадрат,

Брось на формулу свой взгляд,

В ней квадрат гипотенузы

Подведёт итог союзу.

Боги были терпеливы,

Благосклонны, молчаливы.

Он послал им в дар быка,

Чтоб не гневались века.

Современные потомки –

И мальчишки, и девчонки

Учат весело, с задором

Теорему Пифагора.

 

VIII. Значення теореми Піфагора.

   Учитель. Тепер поміркуйте, чому землеміри Стародавнього Єгипту для побудови прямого кута використовували такий спосіб: брали мотузку, ділили її вузликами на 12 рівних частин і кінці зв’язували. Потім мотузку натягували на кілки, щоб отримати трикутник зі сторонами 3, 4 і 5.

   Так за 1500 років до Піфагора, жителі Стародавнього Єгипту знали, що трикутник зі сторонами 3, 4 і 5 є прямокутним і користувалися цим для побудови прямокутників. Такий трикутник називався єгипетським. Інформацію про прямокутний трикутник також знали люди, коли будували ще до Піфагора чудові храми в Єгипті, Вавилоні, Китаї, Мексиці. Ще раніше теорема була відома в Індії.

   Так стародавні єгиптяни, вавилоняни та інші народи Стародавнього Сходу ще за 2000 років до нашої ери знали, що трикутник зі сторонами 3, 4 і 5 – прямокутний.

   Як бачимо, Піфагор не відкрив сформульовану в теоремі властивість прямокутного трикутника, а помітив, узагальнив і довів, перевів з практичної галузі в наукову. Можливо, що Піфагор дав перше повноцінне доведення цієї теореми.

   Цікаво, що саме такі пропорції 3 : 4 : 5 археологи знаходять в розмірах тесаних плит піраміди Херфена в Єгипті.

   Стародавній спосіб побудови прямих кутів іноді застосовується на будівництві і тепер.

 

 

«Філософи» (5-а група) про внесок Піфагора у створення наукової бази             

   Піфагор першим із грецьких математиків вивчав пропорції та найпростіші прогресії. Піфагорійці розглядали три види прогресій: арифметичну, геометричну, гармонічну. Другою визначною геометричною теоремо, яку історики приписують Піфагору, є теорема про суму мір кутів трикутника, що дорівнює мірі двох прямих кутів.

   Піфагор перший використав метод доведення від супротивного, він створив елементарні принципи побудови правильних многогранників, які називав космічними фігурами. Вперше розробив математичну теорію музики. Він вважав, що куля – найдосконаліша з усіх геометричних тіл і що Земля повинна мати форму кулі.

   Особливу увагу Піфагор приділяв числам. Він вважав, що 1 – означена початком всього; 2 – означає протяжність» 1,2,3,4 – відповідають точці, прямій, квадрату і кубові; число 5 символізує колір; 6 – холод; 7 – розум, здоров’я та світло; 8 – кохання, дружбу; 9 – постійність; 10 = 1 + 2 + 3 + 4 – ідеальне число. 10, згідно піфагорійському вченню,  –  таке число на яке можна перевести всі предмети і явища природи з його протилежностями; 13 і 14 були ненависними числами. Піфагорійці розрізняли такі види чисел: добрі числа – непарні; злі числа – парні; числа досконалі – числа, що дорівнюють сумі своїх множників (6 = 1 + 2 + 3); дружні числа – такі числа, одне з яких дорівнює сумі всіх дільників іншого, але без самого числа ( 220 = 1 + 2 + 4 + 71 + 142 та 248) та навпаки        ( 220  та  248 = 1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 4 + 55 + 110); числа пірамідальні; числа многокутні та інші.

   Вони з’ясували, що сума кількох послідовних непарних чисел, починаючи з одиниці, дорівнює квадрату їх кількості                         ( 1 + 3 = 2² = 4).

    Найстрашнішою клятвою в піфагорійців вважалася клятва числом 36, що має такі властивості: 36 = 1³ + 2³ + 3³,                        36 = (1 + 3 + 5 + 7) + ( 2 + 4 + 6 + 8).

      Прямокутні трикутники, сторони яких виражаються натуральними числами, називаються піфагоровими трикутниками. Піфагорових трикутників є безліч. Це, наприклад, прямокутні трикутники зі сторонами 5, 2, 13, або 7, 24, 25, або 13, 14, 15 і т. д.

 

   Піфагор прославився як філософ. Йому належать вислови, які й сьогодні не втратили своєї актуальності.

• Живи з людьми так, щоб твої друзі не стали недругами, а недруги стали друзями.
• Твори велике, не обіцяючи великого.
• Коли хочеш спати, не заплющуй очей, поки не проаналізуєш свої вчинки за минулий день.
• Тимчасова невдача краща за тимчасовий успіх.
• Не роби нічого ганебного ні в присутності інших, ні таємно.
• Лише неблагородна людина здатна в очі хвалити, а поза очі злословити.
• Роби лише те, що в майбутньому не засмутить тебе.
• Все впорядковується відповідно числам.

 

   ІХ. Підсумок уроку.

 

• Кросворд.

 

		1.			П
				2.	І
			3.		Ф
				4.	А
					5.Г
6.					О
			7.		Р

 

1. Назва прямокутного трикутника зі сторонами 3, 4, 5. (єгипетський)
2. Сторона прямокутного трикутника, яка лежить напроти прямого кута. (гіпотенуза)
3. Ім’я, яке прийняла мати Піфагора після того, як збулося пророцтво оракула. (Піфіада)
4.  Острів, на якому народився цей математик. (Самос)
5. Країна, в якій жив Піфагор. (Греція)
6. Місто, в якому цей математик пробув 12 років у полоні. (Вавилон)
7. Ім’я першого вчителя Піфагора який навчав його основам музики та живопису. (Гермодамас)

 

• Оцінювання роботи учнів з аргументацією.
• Вихідна рефлексія.

1. Що сьогодні на уроці було найважливішим?
2. Що на уроці було цікавим?
3. Що викликало ускладнення, труднощі?
4. Над чим слід попрацювати вдома?

   Учитель. Попереду у вас ще багато різних життєвих та геометричних теорем, але сьогодні ви стали дорослішими на цілу теорему – теорему Піфагора – цікаву, могутню й вічну.

 

Життя – театр, а всі ми в нім актори,

Ми знаємо багато різних див,

Та пам’ятати будем Піфагора,

Що теорему «золоту» створив.

Вивчай в житті ще й інші теореми,

Щоб звався ти ученим джентльменом,

То й з розумом не матимеш проблеми

І виростеш культурним бізнесменом.

Сьогодні все. Вам, друзі , на прощання

Рекомендовано домашнєє завдання,

Над геометрією хай ніхто не плаче,

А краще хай розв’язує задачі.

 

Х. Домашнє завдання.

 

 

Підбиття підсумків проекту.

 

                                Хоча чужі знання можуть нас чогось навчити

                                           Мудрим стаєш лише власною мудрістю.

       М. Монтен

 

   Працюючи над проектом, учні повинні були попрацювати над ключовим питанням: « Що може зробити одна людина для всього людства, якщо вона прагне досконалості?»

   Спробуємо обговорити це питання.

   Піфагор найбільш знаменитий учений на всю історію людства. Він був засновником першої наукової школи. Унікальною людиною, «володарем душ»,провідником власної «піфагорійської етики». Піфагор навчив людину вірити в силу розуму, в можливість пізнати світ, вселив у впевненість у тому, що ключем до пізнання світу є математика. Не знатність, не багатство, а ясний розум та чиста совість найбільше цінувалися в піфагорійській школі

   Кожен із нас рано чи пізно, але замислюється над тим, який слід залишить на землі після себе. Для того, щоб залишити по собі світлу пам'ять, необхідно щодня прагнути досконалості, багато працювати над собою.

   Пам’ятайте: надія на успіх живе в кожному із нас, але не кожна надія виправдовується, успіх гарантований лише тим, хто докладає до його здійснення власні зусилля.

 

Ось і закінчився наш проект.

Час невпинно й швидко так летить.

Ви до знань зробили новий крок.

Хай у всьому завжди вам щастить!

Дякую, що працювали гарно,

Часу ви не витрачали марно,

Свої сили і знання доклали.

І проект свій збудували.

 

 

 

Література:

 

1. Про математику і математиків / Упоряд.: А. С. Зоря, С. М. Кіро. – К.: Рад. Школа, 1981. – 254 с.
2.  Математика в школах України. - №33(156),2006.
3. Математика. Довідник / Упоряд.: Г. М . Якушєва; 1997. – 576с.
4. Конфорович А. Г. Визначні математичні задачі. – К.: Рад. Школа, 1981. – 189 с., іл.
5. Інтернет.
6. Видатні вчені. Ілюстрована енцеклопедія для дітей. – Харків: ТОВ, 2010. – 80с.
7. У світі математики: Зб. Наук.-попул. Статей / За ред. М. Й. Ядренка. – К.: Рад. Школа, 1983. – Вип. 14. – 255 с., іл.