Проєктна діяльність з використанням задач економічного змісту для учнів 10-11 класів «Економічна математика в народному господарстві та побуті»

Про матеріал

Єдність теорії та практики – це один із основних принципів педагогіки. Зв'язок математики з іншими дисциплінами, зокрема з економікою, є важливим засобом реалізації цього принципу, тому курс математики повинен мати прикладну спрямованість. Сюжетом прикладної задачі є реальна ситуація, яка пов’язана з професійною чи побутовою діяльністю людини. Застосування прикладних задач найбільш повно реалізується при використанні проєктних технологій.

Перегляд файлу

2862_977

5d5fda3593401403667781

Проєкт

«Економічна математика в народному господарстві та побуті»

(10 – 11 класи)

Усіма можливими способами треба

запалювати в дітях палке прагнення

до знань і до уміння їх здобувати.

Я.А.Каменський

Метод проєктів – це освітня технологія, спрямована на здобуття учнями знань у тісному зв'язку з реальною життєвою практикою, формування в них специфічних вмінь та навичок завдяки системній організації проблемно-орієнтованого навчального пошуку.

Метод проєктів має велике значення для розвитку особистості. Метод дозволяє:

1) навчити учнів самостійно працювати з додатковою літературою;

2) вчити вміння самостійно працювати над творчими завданнями;

3) підвищити інтерес учнів до вивчення математики;

4) виховувати повагу, вміння працювати в колективі;

5) формувати власну життєву позицію;

6) перевірити та закріпити на практиці теоретичні знання;

7) забезпечити продуктивний зв'язок теорії та практики у процесі навчання;

8) набути життєвого досвіду;

9) розвивати вміння аналізувати, систематизувати, узагальнювати вивчений матеріал;

10) здійснювати організовану пошукову, дослідницьку діяльність на підставі спільної праці учнів.

Учень, працюючи над проєктом, проходить стадії планування, аналізу, синтезу, активної діяльності. При організації проєктної діяльності можлива не тільки індивідуальна, самостійна, але й групова робота учнів. Це дозволяє здобувати комунікативні навички й уміння. Постановка завдань, розв’язок проблем підвищує мотивацію до проєктної діяльності й припускає:

цілепокладання, предметність, ініціативність, оригінальність у рішенні пізнавальних питань, неординарність підходів, інтенсивність розумової праці, дослідницький досвід.

Актуальність і значення проблеми. Одним із шляхів розв'язання проблеми є розробка інноваційного методичного забезпечення процесу формування уявлень учнів про можливість і доцільність прикладних застосувань шкільного курсу математики.

Мета проєкту: формування системи знань прикладного використання математичних інструментів в різних галузях народного господарства та в побуті кожної людини через систему розв’язування задач.

Результати проєкту. Система практично орієнтованих навчально-методичних засобів вивчення шкільного курсу математики, спрямованих на формування в учнів життєвих компетентностей щодо використання математичних знань у різноманітних життєвих ситуаціях.

Завдання, які потрібно реалізувати в проєкті:

- сприяти формуванню у школярів системи знань, умінь та наскрізних освітніх компетентностей та відповідних навичок прикладного використання інструментів математичного дослідження процесів та явищ оточуючої дійсності;

- розвивати вміння осмислювати можливість та доцільність застосування математичних моделей та відповідних понять як інструментів застосування здобутих знань на практиці, аналізувати результати обчислень, робити відповідні узагальнення, порівняння, висновки та прогнозувати очікувані результати математичних способів дослідження дійсності.

Економічна математика в промисловості

АТ «Силует» випускає два види продукції (А і В). Для виготовлення 1 од. виробу А потрібно витратити 2 м тканини 1-го типу, 3 м тканини 2-го типу та 1 м тканини 3-го типу; для виготовлення 1 од. виробу в – ті самі тканини із витратами відповідно 1 м, 4 м і 3 м. Виробництво забезпечене сировиною у кількості 400 м, 900 м і 600 м відповідно. Вартість виробу А становить 60 грн. а виробу В – 40 грн.. Складіть план виробництва виробів А і В, який забезпечить максимальний прибуток від реалізації. (Математичне моделювання)

62258258_2323084721088535_2089022627636051968_n

2. Пекарні потрібно закупити олію. Одна фірма пропонує олію по 5 грн. за літр і 8% від вартості усієї купленої олії за транспортування, а друга – по 4,5 грн. за літр і 10% за транспортування. У якій фірмі вигідніше купувати олію? (Відсоткові розрахунки)

f4c6cc_0c04836bd9c64d8dae59fd28b339b997_mv2_d_2760_1616_s_2

У січні підприємство виготовило 750 одиниць продукції, у лютому – 800 одиниць, у березні – 780 одиниць.

А) На скільки відсотків збільшилось виробництво продукції в лютому порівняно із січнем?

Б) На скільки відсотків зменшилось виробництво продукції в березні порівняно з лютим? (Відсоткові розрахунки)

549-678x381

Маркетологи провели дослідження та визначили залежність доходу підприємства від ціни на його продукцію. Було встановлено, що тижневий дохід R є функцією ціни Р: ТR = f (P) = -5P + 10P +3. Визначте ціну продукції, при якій загальний дохід (ТR) підприємства буде максимальним. (Квадратична функція)

571da26-625

Економічна математика в сільському господарстві

Припустимо, що раціон тварин складається із двох видів корму – сіна та концентратів. У таблиці подано числові дані про собівартість кормів у господарстві (у грн..). добова потреба кормів на одну тварину – 20 од. Знайдіть найдешевший щоденний раціон, якщо для сільськогосподарських тварин він повинен включати не менше 16 кг сіна. (Математичне моделювання)

Вид корму

Вміст кормових одиниць на 1 кг кормів

Собівартість кормів(грн.)

Сіно

0,5

1,5

Концентрати

1,0

2,5

Сівалка обладнана ящиком, що вміщує 250 кг зерна. Якою повинна бути ширина захвату сівалки, щоб за швидкості 3,2 км / год. і норми висіву 125 кг зерна на 1 га зерна у ящику вистачило б не більше ніж на 2 год. роботи сівалки, а за швидкості 4 км / год. і тієї є норми висіву – не менше ніж на 1,25 год. роботи? (Математичне моделювання)

З першої ділянки зібрали 2880 ц пшениці, а з другої, площа якої на 12 га менша, - 2160 ц. Знайдіть площу кожної ділянки, коли відомо, що з кожного гектара першої ділянки зібрали пшениці на 4 ц більше, ніж з кожного гектара другої. (Математичне моделювання)

Результат пошуку зображень за запитом "збирають пшеницю"

Економічна математика в побуті

de7c351a1955fe90ad8ad84a42ea48ab

Відомо, що 1 кг м’яса містить 140 г білків, 1 кг молока – 30 г білків. Згідно з нормами харчування добова норма білків має становити не менше 70 г. Ціна 1 кг м’яса становить 40 грн., 1 кг молока – 5 грн.. скільки м’яса та молока необхідно споживати щоденно, щоб за мінімальних витрат у раціоні було не менше 160 г м’яса та не менше 500 г молока на день? (Математичне моделювання)

Скільки потрібно квадратних плиток зі стороною 15 см, щоб застелити підлогу ванної кімнати, розміри якої 3,3 м х 2,8 м ? (Математичне моделювання)

1597_one_max

Якщо взяти 0,4 т свіжих яблук, то вийде 76 кг сушених. Скільки можна одержати сушених яблук з 2,4 т свіжих? (Відношення і пропорції)

Із прямокутного листа жерсті, розміри якого 30 см х 48 см, потрібно виготовити відкриту коробку. Для цього по кутах прямокутника вирізають квадрати. А потім загинають краї листа (рис. 3). Знайдіть, якою завдовжки має бути сторона вирізаного квадрата, щоб площа дна коробки дорівнювала 1008 см² (Математичне моделювання)

x30Idt3vYJd29Sb4osiZhG1VZLqa2g484g7MteRd

ВИСНОВОК ПО ЗАКІНЧЕННЮ ПРОЄКТУ

Розв’язування задач прикладного спрямування сприяє формуванню у школярів системи знань, умінь, освітніх компетентностей та відповідних навичок прикладного використання інструментів математичного дослідження процесів та явищ оточуючої дійсності.

Учасники проєкту мають змогу розвивати вміння осмислювати можливість та доцільність застосування математичних моделей та відповідних понять як інструментів застосування здобутих знань на практиці, аналізувати результати обчислень, робити відповідні узагальнення, порівняння, висновки та прогнозувати очікувані результати математичних способів дослідження.

Завдяки таким завданням учні бачать, що математика знаходить застосування в професійній і побутовій діяльності людини, а це, в свою чергу, прищеплює інтерес до предмета.

Отож, метод проєктів – це ще одна із форм групової роботи, яка полягає в стимулюванні інтересу учасників проєкту (учнів та вчителів) до їхньої самостійної діяльності, постановці перед ними цілей і проблем, рішення яких веде до появи нових знань та умінь. І головне, вона подобається учням.

Використані джерела

Авраменко О.В., Лутченко Л.І., Ретунська В.В., Річняк Р.Я., Шлянчак С.О. «Інноваційні та сучасні педагогічні технології навчання математики», Кіровоград – 2009.

Ткач Ю.М. Математика. Задачі економічного змісту в математиці: Навчально-методичний посібник: / Ю.М. Ткач. – Х.: Вид-во «Ранок», 2011. -176 с. – (Курс за вибором).

Остапович З.П. Проектна технологія навчання на уроках математики. /Авт.- упоряд. Остапович З.П. – Острог, 2018. – 94 с.

Результат пошуку зображень за запитом "проект промисловості"

Пов’язане зображення

Додаток 1.

Розв’язки до завдань проєкту

Економічна математика в промисловості

Задача 1. Етапи розв’язання задачі:

Складемо математичну модель задачі.

Нехай х₁ – кількість виробів А, х₂ – кількість виробів В, які сплановано до виробництва (,). Тоді тканини 1-го типу потрібно буде витратити 2х₁ м на виріб А і х₂ на виріб В; Увесь запас тканини 1-го типу дорівнює 400 м, тобто ; аналогічно для 2-го типу тканини: ; для 3-го типу тканини: . Після реалізації виробів буде одержано (60х₁+40х₂) грн..

Таким чином, потрібно знайти такі х₁ і х₂, щоб виконувалися умови:

(1)

Функція F – цільова функція, х₁ і х₂ – її аргументи, система (1) – обмеження, які описують умови виробництва.

Крім того, лінійна функція F = 60х₁ +40х₂ повинна мати найбільше значення.

Отже, задача полягає в тому, щоб знайти множину розв’язків системи (1) і з неї обрати ті, за яких значення функції F буде найбільшим.

Застосуємо геометричний метод розв’язування задачі. Множиною розв’язків кожної нерівності системи (1) є півплощина; Областю розв’язків даної системи нерівностей є переріз цих півплощин. На рисунку 1 таким перерізом є многокутник ОАБДЕ.

Рис. 1

Найбільшого значення функція F = 60х₁ +40х₂ набуває в одній з вершин цього многокутника: О (0; 0), А (0; 200), В (60; 180), Д (140; 120), Е (200; 0), тому що функція F приймає значення, яке дорівнює с, для всіх пар (х; у) таких що 60х₁ +40х₂ = с. На координатній площині х₁Ох₂ ці точки належатимуть прямій 60х₁ +40х₂ = с. Будемо надавати довільні значення с, при цьому отримаємо різні прямі, які будуть паралельні, оскільки матимуть однаковий кутовий коефіцієнт. Якщо ці прямі будуть проходити через внутрішні точки многокутника ОАВДЕ, то при цьому функція F не набуватиме ні найменшого, ні найбільшого значення. Отже, залишаються прямі, які перетинають многокутник ОАВДЕ тільки по його межі. Таким чином, найбільшого значення функція F = 60х₁ +40х₂ набуває у вершині Д (140; 120) многокутника:

F (140; 120) = 60х₁ +40х₂ = 60 140 + 40 120 = 13 200

х₁ = 140, х₂= 120.

3) Переведемо одержані результати на мову умови задачі та отримаємо, що оптимальним розв’язком буде виготовлення 140 одиниць виробу А і 120 одиниць виробу В; обчислимо максимальний прибуток :

F = 60 140 + 40 120 = 13 200 (грн.)

Відповідь: 13 200 грн.

Задача 2. Нехай пекарні необхідно закупити х кг олії. Розглянемо умови закупівлі олії в обох фірмах.

Якщо олію будуть купувати у першій фірмі, то її вартість буде становити 5х (грн.), витрати на транспортування – 5х 0,08 = 0,4х (грн.). Всього вартість олії – 5х + 0,4х = 5,4х (грн.).

Якщо олію будуть купувати у другій фірмі, то її вартість буде становити 4,5х (грн.), витрати на транспортування – 4,5х 0,1 = 0,45х (грн.). Всього вартість олії – 4,5х + 0,45х = 4,95х (грн.).

Оскільки 5,4х 4,95х, то вигідніше проводити закупівлю олії в другій фірмі.

Відповідь: у другій фірмі

Задача 3. У лютому підприємство виготовило на 50 одиниць ( 800 – 750 = 50) продукції більше, ніж у січні. Знайдемо скільки відсотків становить 50 від 750

У березні виробництво продукції зменшилося на 20 одиниць (800 – 780 = 20)

Відповідь: на %; на 2,5 %

Задача 4. Оскільки ТR = f (P) = -5P + 10P +3 – це квадратична функція, яка має загальний вигляд: у = ах² + вх + с. Для побудови її графіка знайдемо координати вершини параболи за формулою:

ТR = f (P) = -51³+101+3=8,

Координати вершини параболи (1;8)

Побудуємо графік (рис. 2). Графічне зображення функції загального доходу підприємства має вигляд параболи, вітки якої напрямлені вниз. Максимального значення дохід R набуде у вершині параболи. Тобто максимуму функція доходу досягне при ціні Р = 1, тоді загальний дохід ТR = 8.

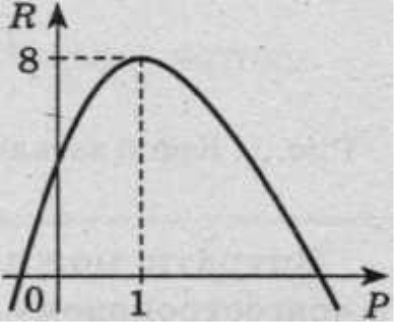
$Описание: C:\Users\-12~1\AppData\Local\Temp\FineReader11\media\image7.jpeg$

Рис. 2

Додаток 2.

Розв’язки до завдань проєкту

Економічна математика в сільському господарстві

Задача 1. Нехай х – кількість сіна, у – кількість кг концентратів. Ураховуючи умову задачі та дані таблиці, запишемо співвідношення: 0,5х + у = 20 – щоденна потреба у кормах на одну тварину; х 16 – щоденна потреба сіна; у0 – кількість концентратів не може бути від’ємною.

Цільова функція z ( функція, мінімум чи максимум якої треба знайти):

z = 1,5х + 2,5у.

Побудуємо графік (рис. 1)

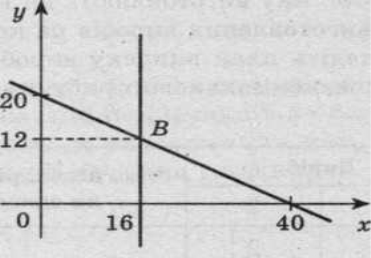
$Описание: C:\Users\-12~1\AppData\Local\Temp\FineReader11\media\image6.jpeg$

Рис. 1

Необхідно визначити мінімальне значення цільової функції при обмеженнях, встановлених вище:

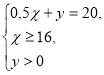
Розв’язавши систему, знайдемо найбільш економний щоденний раціон для однієї тварини: (16; 12). При цьому z (В) = 54.

Відповідь: 54 грн.

Задача 2. Нехай х га – площа першої ділянки. - урожайність з першої ділянки, - урожайність з другої ділянки. Маємо рівняння:

720 ( х – 12) – 540 х – х (х – 12) = 0

х² – 192 х + 8640 = 0

х₁ = 72, х₂ = 120

х₁ – 12 = 60; х₂ – 12 = 108

Відповідь: 72 га та 60 га або 120 га та 108 га.

Задача 3. Помножимо швидкість сівалки на час роботи і дізнаємось шлях, який проїде сівалка: 3,2 2 = 6,4 (км) = 6 400 (м).

Ємкість ящика – 250 кг зерна, норма висіву – 125 кг на 1 га, площа, яку можна засіяти цим зерном дорівнює: 250 : 125 = 2 (га) = 20 000 м. Маємо рівняння: 6400 х = 20 000

х = 3, 125 (м) – ширина захвату.

Якщо швидкість буде становити 4 км / год., то за 1,25 год. сівалка проїде:

41,25 = 5 (км) = 5 000 (м). Зерна вистачить на 2 га = 20 000 м. Маємо рівняння: 5 000 х = 20 000

х = 4 (м) – ширина захвату.

Ширина захвату має бути від 3,125 м до 4 м.

Відповідь: від 3,125 м до 4 м.

Додаток 3.

Розв’язки до завдань проєкту

Економічна математика в побуті

Задача 1. Нехай х – кількість кг м'яса, а у – кількість кг молока. Тоді за умовою задачі складемо такі співвідношення: 0,14 х + 0,03у0,07 – раціон містить 70 г білка; х0,16 – кількість м’ яса не менше 0,16 кг; у0,5 – кількість молока не менше 0,5 кг.

Витрати становлять 40х + 5у. Складемо математичну модель даної задачі: необхідно визначити найменше значення цільової функції z = 40х + 5у, якщо х і у задовольняють умови:

При обмеженнях встановлених вище. Необхідно визначити мінімальне значення цільової функції z ( див. рисунок 1). Отже, у денний раціон необхідно включити 0,16 кг м’яса та 1,59 кг молока. При цьому z (А) = 14,35

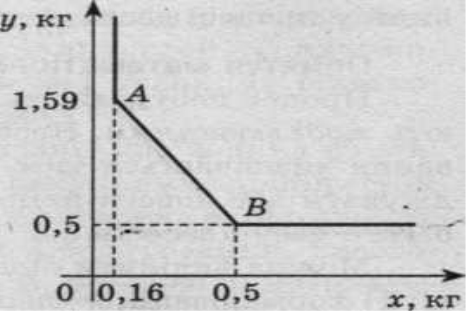
$Описание: C:\Users\-12~1\AppData\Local\Temp\FineReader11\media\image5.jpeg$

Рис. 1

Задача 2. Побудуємо математичну модель задачі. Нехай для застелення підлоги потрібно х плиток. Площа однієї плитки дорівнює

0,15 0,15 = 0,0225 (м² )

Площа х плиток – 0, 0225х м², а площа підлоги – 3,3 2,8 = 9,24 (м²).

Площа усіх плиток має бути не менша від площі підлоги:

0, 0225 х9,24.

Дана нерівність і є математичною моделлю задачі. Розважимо нерівність:

0, 0225 х9,24.

х9,24 : 0,0225

х410, (6)

Запишемо одержаний результат мовою вихідної задачі: щоб застелити підлогу , потрібно не менше ніж 411 плиток.

Відповідь: не менше ніж 411 плиток

Задача 3. Складемо відношення: 0,4 т – 76 кг

2,4 т - х кг.

Маємо пропорцію:

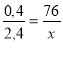
Відповідь: 456 кг

Задача 4. Складемо математичну модель задачі. Нехай х см – сторона вирізаного квадрата. Маємо рівняння:

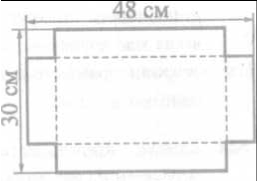
$C:\Users\-12~1\AppData\Local\Temp\FineReader11\media\image3.jpeg$

(30 – 2 х)( 48 – 2 х) = 1008

(х – 15)( х – 24) = 252

х² – 39 х + 108 = 0

х₁ = 3, х₂ = 36

Рис. 2

х₂ = 36 не задовольняє умову задачі, бо перевищує один з розмірів листа.

Відповідь: х =3

docx

Завантажити

Зберегти на потім

Додав(-ла)

Коваль Тамара

Пов’язані теми

Математика, 10 клас, Інші матеріали

Додано

20 листопада 2022

Переглядів

690

Оцінка розробки

Відгуки відсутні