Проектні ідеї та їх використання у класах на прикладі теми "Елементи комбінаторики"

Бердянська вечірня (змінна) школа №1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Проектні ідеї та їх застосування у класах

 

 

 

 

 

 

 

 Виступ на теоретичному семінарі

 вчителя математики

 Старцевої Наталії Володимирівни             

 

 

 

 

 

 

 

Бердянськ-2012

Проект «Елементи комбінаторики»

Тема проекту: Елементи комбінаторики.

Учасники проекту: учні 11 класу.

Тип проекту: практично-орієнтований.

Термін виконання: 2 тижні.

Тип уроку: урок узагальнення і систематизації знань.

Епіграф уроку: «Число, розміщення і комбінація — три взаємно перетинаючі, але різні сфери думки, якими можна описати всі математичні ідеї» (Д. Д. Сильвестр).

I. Актуальність проекту як навчальної технології

Проектне навчання дозволяє розширити коло завдань, які учень розв'язує на уроці, створює умови для творчого розвитку особистості. З'являється елемент зацікавленості у процесі навчання.

II. Мета і завдання проекту

Узагальнити і систематизувати знання з теми: «Елементи комбінаторики», навчити розв'язувати задачі зі сполуками, здійснювати операції над множинами.

Розвивати творче мислення всебічним аналізом проблем, запам'ятовувати інформацію у вигляді логічних структур, розуміти причинно-наслідкові зв'язки.

III. Механізм реалізації проекту

1. Постановка проблеми.

Починаючи вивчати тему «Елементи комбінаторики», важ­ливо зазначити причину виникнення даного розділу математики і її роль у сучасному суспільстві.

2. Визначення тем і мети проектів.

Для захисту пропонують проекти з таких тем: «Історія ви­никнення і розвитку науки комбінаторики», «Цікава комбінато­рика», «Застосування комбінаторики».

Проекти можна подавати у формі презентацій або рефератів.

3. Захист проектів.

Захист проектів проходить у кінці вивчення теми.

4. Оцінювання проектів.

Оцінювання проводить вчитель, враховуючи і якість самих проектів, і відповіді учнів, під час уроку.

 

Хід уроку

1. Організаційні питання.

2. Перегляд проекту «Історія виникнення і розвитку науки комбінаторики».

Орієнтовний опорний конспект проекту

Комбінаторика — гілка математики, що вивчає комбінації та перестановки предметів — виникла XVII ст. Із задачами, в яких доводиться вибирати ті чи інші предмети, розміщувати їх в пев­ному порядку і відшуковувати серед різних розміщень найкращі, люди стикнулися ще в доісторичну епоху, обираючи найкращі розміщення мисливців під час полювання, воїнів під час битви, інструментів під час роботи. Певним чином розташовувалися при­краси на одязі, візерунки на кераміці. З ускладненням виробни­чих і суспільних відносин ширше доводилося користуватися за­гальними поняттями про порядок, ієрархію, групування. В тому ж напрямку діяв розвиток ремесел торгівлі. Комбінаторні нави­чки виявилися корисними і в години дозвілля. Не можна точно сказати, коли поряд зі змаганнями з бігу, метання диска, стриб­ках з'явились ігри, що потребували в першу чергу вміння роз­раховувати, складати плани і спростовувати плани противника.

 

Комбінаторика в Єгипті

Серед предметів, покладених в піраміду, де 35 століть тому був похований єгипетський фараон Тутанхамон, знайшли роз­креслену дощечку з трьома горизонталями і 10 вертикалями та фігурки для давньої гри «сенет», про правила якої ми, можливо, ніколи не дізнаємось. Згодом з'явились нарди, шашки й шахи, а також їх різноманітні варіанти (китайські та японські шахи, японські облавні шашки «го» тощо). У кожній із цих ігор доводи­лося розглядати різноманітні комбінації фігур, що мали здатність пересуватись, та вигравав той, хто їх краще вивчив, знав пере­можні комбінації та вмів уникати програшів. Звичайно, в цей період ніхто й не здогадувався про науку, що розглядає рішення комбінаторних задач.

Комбінаторика в Китаї

Перша згадка про питання, близькі до комбінаторних, зустрі­чається в китайських рукописах, що відносяться до ХІІ-ХІІІ ст. до н. е. У цих книгах написано, що усе в світі є поєднанням двох початків — чоловічого та жіночого, які автори позначали сим­волами «інь» та «янь». У рукописі «Же-ким» («Книга перемін») показані різні з'єднання цих знаків по два і по три. Вісім малюнків з трьох рядів символів відображали землю, гори, воду, вітер, грозу, вогонь, хмари і небо. Сума перших 8 натуральних чисел (тобто число 36) втілювала в уяві стародавніх китайців весь світ. Згодом виникла потреба виразити й інші елементи за допомогою знаків «інь» та «янь». Були складені 64 фігури, що складалися з п'яти рядів рисочок.

У рукописі «Же-ким» є і більш складні малюнки. Як ствер­джує переказ, імператор Ію, котрий жив приблизно 4000 років тому назад, побачив на березі річки священну черепаху, на пан­цирі якої був зображений малюнок з білих і чорних кружків. Якщо замінити кожну фігуру відповідним числом, з'являється така таблиця, де при додаванні чисел в кожному рядку, стовп­чику та по діагоналі отримаємо одне і те саме число 15.

 

Комбінаторика в Древній Греції

Конкретні комбінаторні задачі, що торкалися перерахунку невеликих груп предметів, греки розв'язували без помилок. Арістотель описав без пропусків всі види правильних тричленних си­логізмів, а його учень Аристоксен з Тарента перерахував різнома­нітні комбінації довгих і коротких складів у віршових розмірах. Математик Папп (IV ст. н. е.) роздивлявся число пар і трійок, які можна отримати з трьох елементів.

Напевно, у грецьких вчених були якісь невідомі нам, правила комбінаторних розрахунків, які швидше за все були невірними.

Схоласт Раймонд Люллій створив у ХШ ст. машину, що складалася з кількох кіл, на які було нанесено основні предика­ти, суб'єкти, атрибути та інші поняття схоластичної логіки. По­вертаючи ці кола, він отримував різні суміщення понять і споді­вався отримати з їх допомогою істину.

Комбінаторика в країнах Сходу

У VIII ст. н. е. почався розквіт арабської науки. Араби пе­реклали багато творів грецьких учених, вивчили їх, а потім досягли успіхів у науці про розв'язання рівнянь (саме слово «ал­гебра» — арабського походження), теорії та практиці обчислень. Вирішуючи питання про знаходження коренів з будь-якого степе­ня, арабські алгебраїсти вивели формулу для степеня суми двох чисел, яка відома під не зовсім правильною історичною назвою «біном Ньютона». Напевно, саме цю формулу знав поет і мате­матик Омар Хайям (ХІ-ХП ст. н. е.).

Роботи Паскаля і Ферма дали поштовх для народження двох нових гілок математичної науки — комбінаторики і теорії ймовір­ностей. Якщо до них комбінаторні проблеми порушувалися у загальних працях із астрології, логіки і математики, що значною мі­рою вважалось математичною розвагою, то вже у 1666 р. Готтфрід Вільгельм Лейбніц публікує «Дисертацію про комбінаторне мисте­цтво», в котрій вперше з'явився термін «комбінаторика». Проек­ти Лейбніца здавалися нездійсненними тогочасним математикам, але тепер, після створення ЕОМ, багато планів Лейбніца почали втілюватися у життя, а дискретна математика виросла настільки, що вступило в суперечку із класичним математичним аналізом.

В 1713 р. була опублікована книга «Мистецтво припущень» Якоба Бернуллі, в якій вказувались формули для числа розмі­щень з п елементів по к, виводились вираження для степеневих сум тощо. Чудові досягнення в області комбінаторики належать одному з найбільших математиків XVIII ст. Леонарду Ейлеру, швейцарцю, що прожив майже все життя в Росії, де був членом Петербурзької академії наук. Основна частина наукової роботи Ейлера присвячена математичному аналізу, в якому він проклав нові шляхи, створив цілий ряд нових областей.

Після робіт Паскаля і Ферма, Лейбніца і Ейлера можна було вже говорити про комбінаторику як про окрему, самостійну гілку математики, тісно пов'язану з іншими областями науки, такими, як теорія ймовірностей, вчення про ряди тощо. У кінці XVII ст. німецький учений Гінденбург та його учні зробили спробу побуду­вати загальну теорію комбінаторного аналізу. Проте вона не мали успіху — в той час ще не було накопичено достатньої кількості важливих і цікавих задач, які могли б дати необхідний фунда­мент для такої теорії.

3. Актуалізація опорних знань.

Технологія «Продовж речення».

На дошці написано завдання, учні на вибір вчителя підхо­дять і дописують відповідь.

 

= ……………

= ……………

= ……………

= ……………

 

Технологія «Мозаїка».

На дошці зображена схема. Учень отримує вирази на аркушах, йому треба скласти правило вибору формули для розв'язування задач із комбінаторики.

 

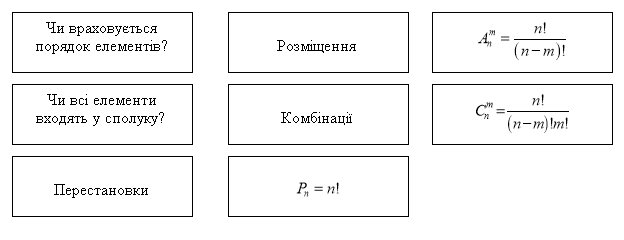
4. Перегляд проекту «Цікава комбінаторика».

Орієнтовний опорний конспект проекту

Професор Отто Ліденброк — головний герой роману Жуля Верна «Подорож до центру землі», в букіністичній крамниці на­трапив на манускрипт XIII ст., написаний рунічним письмом. (Руни — письмові знаки, що вживалися в середньовіччі і, за легендою, були винайдені самим Одіном — верховним богом в ісландській міфології). Але зацікавила Отто записка, залише­на в цій книзі її колишнім власником, знаменитим алхіміком XVII ст. Анре Сакнуссемом. Сумніву не було: у записці йшлось про якесь велике відкриття. І хоча запис було зроблено добре відомим професору рунічним письмом, проте прочитати його не вдалось. Повідомлення було зашифровано. Прочитати його можна було лише двома способами: або розглянути всі варіанти розмі­щення 20 рунічних знаків, або знайти ключ до шифру. Як ви думаєте, яким способом Отто Ліденброк прочитав записку?

Його асистент Аксель підрахував, що переставляти руніч­ні знаки професору довелося б 2 32 902 008 176 640 000 раз. (В. О. Тадєєв «Неформальна математика» Тернопіль, 2003).

Комбінаторика дозволила прочитати і крито-мікенське ліній­не письмо. Перші надійні основи розшифровки цієї писемності заклала Аліса Д. Кобер, яка захистила у 1932 р. докторську дис­ертацію з математики у Колумбійському університеті. Поряд із дослідженнями з чистої математики, вона багато зусиль доклала до розшифровування давніх писемностей. Вивчивши знаки крит­ського письма, Аліса встановила, що це письмо складається зі складів. Кобер отримала координатну сітку, в якій замість осей координат стояли номери голосних і приголосних літер. У цієї сітки був лише один недолік — ніхто не знав, які саме голосні та приголосні формують цю систему координат. Лише через два роки після смерті дослідниці молодий англійський архітектор Майкл Вентрис, розширюючи її координатну сітку, спробував вгадати значення деяких голосних (число голосних менше числа приголо­сних). Одна із спроб закінчилася вдало — текст заговорив на мові, що нагадував грецьку. Але це не була класична грецька мова «Іліади» та «Одісеї», а грецька мова більш ранньої епохи. Вентрису до­поміг завершити розшифровку видатний знавець ранньої грецької мови Чедвік. Використовуючи імена царів та списки географічних назв, дослідники розшифровували один склад за іншим. А потім почалася швидка розшифровка — три десятки, знаків отримали своє значення. Це був повний тріумф комбінаторного підходу.

Не тільки азартні ігри спонукали математиків до комбіна­торних роздумів. Ще з давніх-давен дипломати, які практику­вали таємне листування, винаходили все більш складні шифри, а секретні служби інших держав намагалися ці шифри розгадати. Одним із найпростіших шифрів була «тарабарська грамота», в якій літери замінювались іншими за певними правилами. Про­те такі шифри легко розгадувалися за характерним поєднанням літер. Тому почали застосовувати шифри, які ґрунтувалися на комбінаторних методах, наприклад, на різних перестановках літер, заміна літер з використанням ключових слів тощо. Для кодування та розшифровки залучались математики. Ще в кінці XVI ст. розшифровкою листувань між ворогами французького ко­роля Генріха ІІІ та іспанцями займався один із творців сучасної алгебри Франсуа Вієт. А в Англії XVII ст. монархічні заколо­тники дивувались швидкості, з якою Кромвель розгадував їх за­думи. Монархісти вважали шифри, якими вони користувались у листуванні, нерозшифрованими, і вважали, що ключі до них були видані кимось із учасників заколоту. І лише після падін­ня республіки та царювання Карла II вони дізналися, що всі їх шифри розгадував один із кращих англійських математиків того часу, професор Оксфордського університету Уолліс, котрий мав винятковий комбінаторний талант. Він назвав себе засновником нової науки «криптографії». Шифрами користувались не тільки дипломати і заколотники, але й самі вчені. До XVII ст. майже не існувало наукових журналів. Вчені дізнавалися про досягнення своїх колег із книг або приватних листів. Це створювало великі труднощі при опублікуванні нових результатів — адже видання книг займало роки, а написати про свої відкриття у листі було ризиковано — хтось міг присвоїти винахід. Тому між ученими часто виникали суперечки на тему переваг. Ще в кінці XVII ст. йшли довгі суперечки.

У давнину Архімеду доводилося хитрувати. Коли дехто з олександрійських вчених присвоював собі його результати, описані у листах, він писав їм ще одного листа, який складався з формул для обчислень об'ємів та площ різних фігур і тіл. Вчені стверджували, що ці формули їм давно відомі і нічого нового Архімед їм не повідомив. Але тут з'ясовувалось, що усі ці формули неправильні. Для того, щоб забезпечити пріоритет і не допустити передчасного розголосу отриманих результатів, вчені в короткій формі формулювали суть відкриття, а потім переставляли літери і відправляли листа з переставленими літерами своїм колегам. Такі тексти з переставленими літерами називалися анаграмами.

Навички в розгадці складних шифрів допомогли ученим, коли археологи почали знаходити камені та черепи з таємними знака­ми. Одним з найбільших успіхів у розшифруванні було прочитання французьким філологом Жаном Франсуа Шамполем ієрогліфів, яки­ми писали єгиптяни ще до того, як виникла наука у древніх греків.

Технологія «Лото».

На дошці аркуш паперу із відповідями. Учням роздають на ар­кушах завдання із операціями над сполуками, які написані з одного боку аркуша і з елементами малюнка з другого боку. Розв'язавши завдання, учень наклеює свій елемент, малюнка на місце, де на­писана його відповідь. У результаті школярів отримують повний малюнок, що свідчить про правильне розв'язування завдання.

Завдання

1.            Відповідь:
2.                Відповідь:
3.                 Відповідь:
4.                Відповідь:
5.       Відповідь:
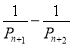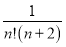
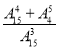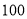
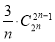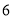
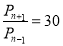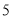
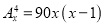6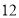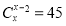.                Відповідь:

 

 

5. Перегляд проекту «Застосування комбінаторики».

Орієнтовний опорний конспект проекту

Комбінаторика — важливий розділ математики, знання яко­го необхідні працівникам різноманітних спеціальностей. З ком­бінаторними задачами доводиться мати справу фізикам, хімікам, біологам, лінгвістам, спеціалістам із кодів тощо. Комбінаторні ме­тоди лежать в основі рішення багатьох задач теорії ймовірностей та її застосувань.

Комбінаторика в біології

Складність будови біологічних систем, їх сувора ієрархічність, взаємопоєднання окремих процесів в цілому організмі ро­блять біологію придатною для застосування комбінаторних мето­дів. Радянський біолог А. А. Любищев припускав навіть, що схо­жість рослин та морозних візерунків на вікнах не випадкове — в обох випадках проявляються певні закони комбінування частин в одне ціле. Коли біологи почали вивчати передачу генетичної інформації у бактерій, то помітили, що в процесі цієї передачі хромосоми переходять від однієї бактерії до іншої не повністю. Вони сподівалися, вивчаючи частини, що перейшли з однієї бак­терії до іншої, визначити порядок розміщення генів у хромосомі. Але карти хромосом, складені в різних лабораторіях, були несхо­жими одна на одну. Проте, детально порівнявши отримані карти, французькі учені Жакоб та Вальмон помітили їх комбінаторну схожість. Виявилося, що всі ці карти були частинами одного кільця — хромосоми бактерій виявлялись згорнутими у кільця, які перед переходом у іншу бактерію розриваються, після чого до одного кінця прикріплюється фактор, що перетягує хромосо­му з однієї бактерії до іншої. А так як розірватися кільце могло у будь-якому місці, а фактор міг прикріпитися до будь-якого кін­ця, то й виникало багато різних карт, котрі заплутували картину.

Однією з найбільш складних загадок в біології XX ст. була будова «ниток життя» — молекул білка і нуклеїнових кислот. Виявилося, що молекули білка — це об'єднання декількох довгих ланцюгів, що складалися з 20 амінокислот.

Поєднуючи комбінаторні розгляди з вивченням рентгенів­ських знімків, вченим вдалося розгадати будову багатьох білків, в тому числі гемоглобіну, інсуліну тощо.

Найбільшим досягненням комбінаторного підходу до проявів життя можна вважати розшифровку будови дезоксирибонуклеї­нової кислоти (ДНК), зроблену в Кембриджі Ф. Криком та Дж. Уотсоном у 1953 р.

Комбінаторика в хімії

17 лютого 1869 р. з хаосу хімічних елементів, кожен з яких мав свої властивості, виникла таблиця — був відкритий періо­дичний закон. Це відкриття було зроблено Дмитром Івановичем Менделєєвим, професором Петербурзького університету. Готую­чи курс лекцій із загальної хімії, він задумався над порядком, в якому потрібно було розповідати про елементи.

Як писав згодом сам вчений, «шукати щось, хоча б гриби, чи якусь залежність, можна, як дивлячись та пробуючи». Для того, щоб «дивитися і пробувати», він почав підбирати, написавши на окремих картках, назви елементів з їхніми атомними масами та властивостями даного елемента, схожі елементи та атомні маси.

Розкладуючи свій хімічний пасьянс, великий вчений після напружених роздумів знайшов правильне розміщення елементів. Кажуть, що кінцевий вигляд таблиці постав перед ним уві сні, коли, стомлений безперервною роботою над нею, він приліг відпочити. Вражає, що відкриття було зроблено Менделєєвим за один день — зранку 17 лютого 1869 р. він ще й не починав роз­кладати свій пасьянс, а до вечора того ж дня таблиця була готова.

У фізиці комбінаторика є необхідною при вивчені властиво­стей кристалів, опису моделі феромагнетизму тощо.

 

 

Комбінаторика епохи комп'ютерів

В нашу епоху комбінаторика з області, що цікавила перш за все лише окремих авторів задач та знаходила застосування в ко­дуванні і розшифровці давніх писемностей, перетворилася на об­ласть, що знаходиться на магістральному шляху розвитку науки.

Шифрування, кодування, дешифрування письмової інформації — важливе, але не єдине застосування комбінаторики. Кодами є також державні номерні знаки, штрих-коди.

Цілеспрямований вибір «різних можливих варіантів» необ­хідний для складання розкладу руху транспорту, розкладу занять у школі, а ще як апарат для розв'язку завдань теорії ймовірності.

6. Перевірка умінь і навичок розв'язувати задачі з даної теми.

Самостійна робота (5 хв).

Вчитель роздає задачі на аркушах. 1 варіант — учень виби­рає і розв'язує лише задачу на розміщення; 2 варіант — учень вибирає і розв'язує лише задачу на комбінацію.

1 варіант

1. У групі є 10 осіб. Скількома способами можна вибрати 5 із них для екскурсії?
2. Скількома способами можна вибрати старосту і заступ­ника, якщо в класі 25 учнів?
3. Скількома способами можна вишикувати шеренгу із 5 чоловік.

2 варіант

1. Скількома способами можна розставити 6 стільців навко­ло стола?
2. Скількома способами можна вибрати інструктора і стар­шого інструктора із 30 осіб?
3. Скількома способами можна вибрати  2 чергових із 25 осіб?