Рівнобедрений трикутник та його властивості

Геометрія               

7 клас

Тема: Рівнобедрений трикутник  та його властивості

 Мета:

• здійснити діагностику засвоєння знань та вмінь з теми «Перша та друга ознаки рівності трикутників»;
• ввести поняття рівнобедреного трикутника, його елементів;
• познайомити із теоремою про властивість кутів при основі рівнобедреного трикутника і наслідками з неї;
• ознайомити з означенням рівностороннього трикутника та того факту, що рівносторонній трикутник можна вважати рівнобедреним;
• сформувати первинні вміння,   використовуючи означення, розпізнавати на рисунку або за умовою задачі рівнобедрений трикутник та називати його елементи; використовувати  теорему про властивість кутів при основі рівнобедреного трикутника при розв’язуванні задач; сприяти формуванню вміння застосовувати отримані знання в новій ситуації;
• розвивати уміння виявляти закономірності, робити узагальнення і висновки, розвивати математичне мислення, просторову уяву;
• виховувати математичну культуру учнів, сприяти вихованню інтересу до вивчення математики.

Наочність і обладнання: набір демонстраційного креслярського приладдя; таблиця «Рівнобедрений трикутник», жетони, презентація.

ХІД УРОКУ

I. Організаційний момент

II. Перевірка домашнього завдання

Наявність домашнього завдання перевіряють чергові. Дати відповіді на питання учнів. Зошити з домашнім завданням збираються після уроку. 

 III. Мотивація навчальної діяльності. Формулювання мети й завдань уроку

Оскільки трикутник та його види за сторонами й кутами розглядались у 5 класі, можна звернутись до знань учнів та, активізувавши ці знання, сформулювати мету та завдання уроку.

Сьогодні наше з вами завдання пригадати те, що ми вже знаємо про рівнобедрений трикутник та вивчити його основні властивості, навчитись застосовувати набуті знання при розв’язування задач.

IV. Актуалізація опорних знань

1.               Гра «Вірно-невірно»,  для відповідей використовують червоні та зелені жетони. Кожна правильна відповідь – 1 бал

•                   висота трикутника – це перпендикуляр, опущений з вершини трикутника на протилежну  сторону;
•                   трикутники рівні, якщо два кути одного трикутника дорівнюють двом кутам другого трикутника;
•                   медіана – відрізок, який виходить з вершини і ділить кут на дві рівні частини;
•                   сума двох кутів трикутника дорівнює 120 градусів, чи може  третій кут бути 80 градусів?
•                   зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів не суміжних з ним;
•                   якщо дві сторони і кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними другого трикутника, то такі трикутники рівні;
•                   чи правильно, що трикутник, який має прямий кут називається прямокутним;
•                   медіана – відрізок, який сполучає вершину трикутника і середину протилежної сторони;
•                   будь-який трикутник має 1 бісектрису;
•                   якщо сторона і два прилеглі до неї кути одного трикутника відповідно дорівнюють стороні і двом прилеглим кутам другого трикутника, то такі трикутники рівні;
•                   сума кутів трикутника дорівнює 360 градусів?
•                   чи може існувати трикутник, у якого два кути будуть тупими?

2.               Виконання усних вправ (слайд № )
   1.       Доведіть рівність Δ ABC і ΔMKС (рис. 1).

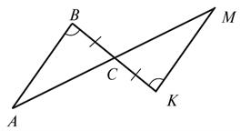Рис.1

2.       Доведіть рівність трикутників ABC і MKC (рис. 2). Слайд №

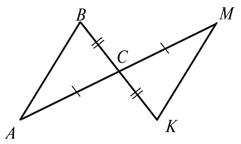Рис.2

3.       Серед трикутників зі вказаними довжинами сторін (рис. 3) виберіть один зайвий. Поясніть свій вибір. Слайд №

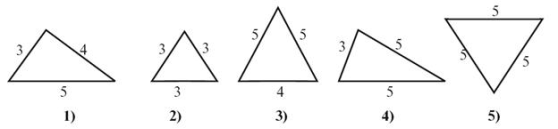Рис.3

V. Засвоєння нових знань

План вивчення нового матеріалу

1°. Означення рівнобедреного трикутника. Його елементи. Периметр рівнобедреного трикутника.

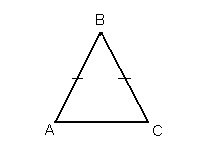Трикутник називається рівнобедреним, якщо в нього дві сторони рівні.

Рівні сторони називають бічними сторонами, а третю його сторону – основою.

Випишіть для цього трикутника бічні сторони і основу.

Рис.4

Периметр рівнобедреного трикутника = 2 бічні сторони + основа.

Р = 2АВ + АС

Для рівнобедрених трикутників на рис.1 знайдіть Р. (Слайд №  )

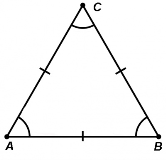2°. Рівносторонній трикутник як особливий випадок рівнобедреного трикутника. Периметр рівностороннього трикутника.

Рис.5

Трикутник, всі сторони якого мають різні довжини, називають різностороннім.

Трикутник, всі сторони якого рівні, називають рівностороннім. Рівносторонній трикутник є окремим видом рівнобедреного трикутника.

Периметр рівностороннього трикутника = довжину сторони помножити на 3. Р = 3а, де а – довжина сторони трикутника.

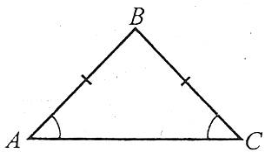3°. Теорема про властивість кутів рівнобедреного трикутника. 

Теорема. Якщо в трикутнику два кути рівні, то він рівнобедрений.

Рис.6

Доведення: Нехай у Δ АВС   <А=<С. Доведемо, що АВ=ВС. Проведемо бісектрису ВК. Вона розбиває даний трикутник на два:ΔВАК і ΔВСК. У них: <А= <С, <АВК=<СВК, тому <ВКА = <ВКС. ВК- спільна сторона, отже, за стороною і двома прилеглими кутами ΔВАК = ΔВСК. І значить, АВ=ВС.

Наслідок. У трикутнику проти рівних сторін лежать рівні кути, а проти рівних кутів – рівні сторони.

VI. Первинне усвідомлення нового матеріалу

Виконання усних вправ

1. Які з трикутників, зображених на рисунку 7, є рівнобедреними?

2. Для рівнобедрених трикутників, зображених на рисунку 7, назвіть основи та бічні сторони. Обчисліть периметр кожного з рівнобедрених трикутників (найзручнішим способом).

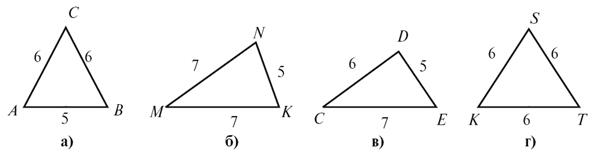
Рис.7

3. Знайдіть периметр рівнобедреного трикутника, якщо бічна сторона дорівнює 6 см, а основа в 3 рази менша;

4. У трикутнику КМL:  KM = ML. Назвіть рівні кути трикутника.

 Рис.8

5. Чому дорівнює кут D трикутника DEF, зображеного на рисунку 9?

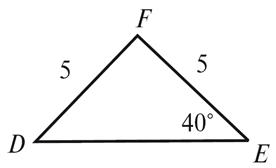  Рис.9

Фізкультпауза

1.               Вправа для очей - " Розфарбовування". Дітям пропонується  закрити очі і уявити перед собою великий білий екран. Необхідно подумки розфарбувати цей екран по черзі будь-яким кольором: наприклад, спочатку жовтим, потім помаранчевим, зеленим, синім, але закінчити розфарбовування треба найулюбленішим кольором.

2.  Вправа " Буратіно". Учням пропонується закрити очі і уявити, що їх ніс виріс, як у Буратіно. Можна запропонувати умочити його, як в казці, в чорнило і намалювати  як можна красивіше носом в повітрі  рівнобедрений трикутник, тупокутний трикутник, дві паралельні прямі. Це можна зробити тільки подумки або з рухом голови; зафіксувати перед очима фігуру, запам'ятати її. Намалюйте трикутник одночасно лівою і правою рукою.

VI. Удосконалення знань, умінь і навичок

На дошці

1.               Периметр рівнобедреного трикутника дорівнює 2,6 м. Знайдіть сторони трикутника, якщо його основа більша від бічної сторони на 0,2 м.
2.               Периметр рівнобедреного трикутника дорівнює 20 см. Знайдіть  сторони трикутника, якщо його бічна сторона відноситься до основи як 3 : 4.

Самостійна робота (картки)

1 варіант

У рівнобедреному трикутнику АВС з основою АС проведено медіану ВК.

Визначте, чи рівні трикутники АВК і СВК.

2 варіант

У рівнобедреному трикутнику АВС з основою АВ проведено бісектрису ВD.

Визначте, чи рівні трикутники ABD і CBD.

VII. Підсумок уроку

Яке число можна поставити замість *, щоб Δ ABC був рівнобедреним:

а) з основою AB; б) з основою AC? Для кожного випадку назвіть рівні кути (рис. 10).

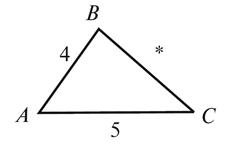Рис.10

Добудуйте трикутник свого настрою.

Це цікаво:

• У стародавньому мистецтві дуже широко поширюються зображення рівностороннього трикутника. Первісні люди  штампували трикутники на різних виробах.
• Вожді племен північно-американських   індійців носили на грудях символ влади: рівносторонній трикутник з крапкою в центрі.
• В Африці жінки  також прикрашають себе великими пластинами                                     рівносторонніх трикутників.
• Рівносторонні трикутники малювали – на зображеннях священних тварин.

VIII. Домашнє завдання. Оцінки з коментуванням.

Прочит. п.13, ст.104, виконати №387,№389 ст.107