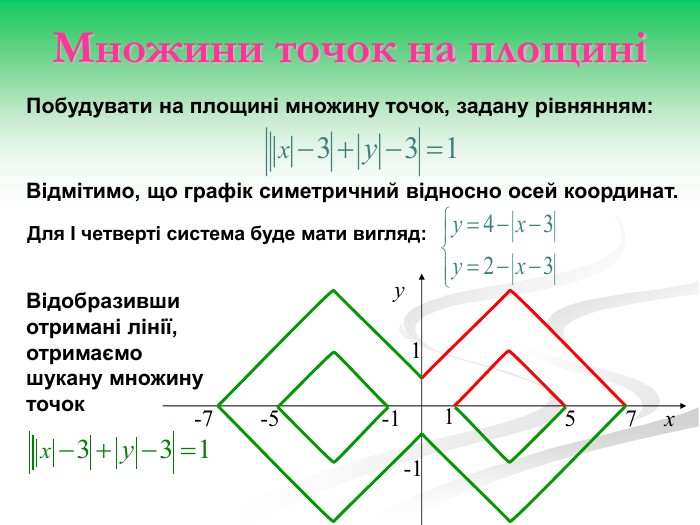
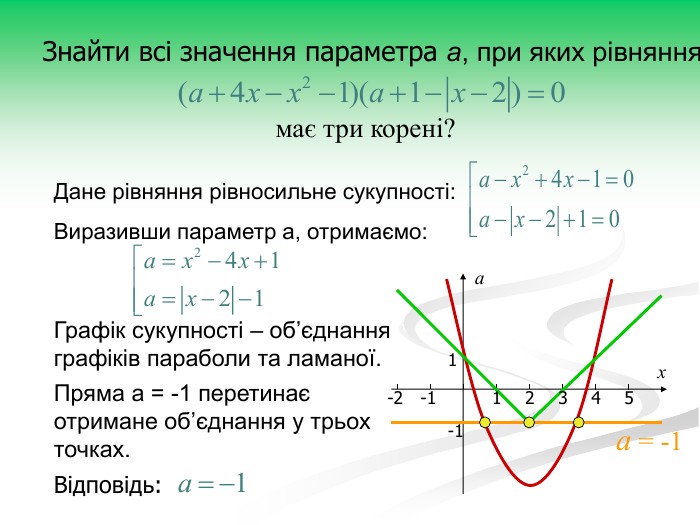
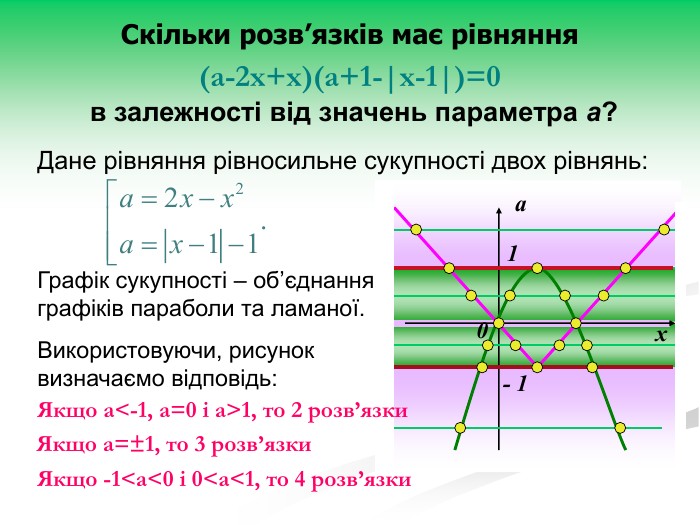
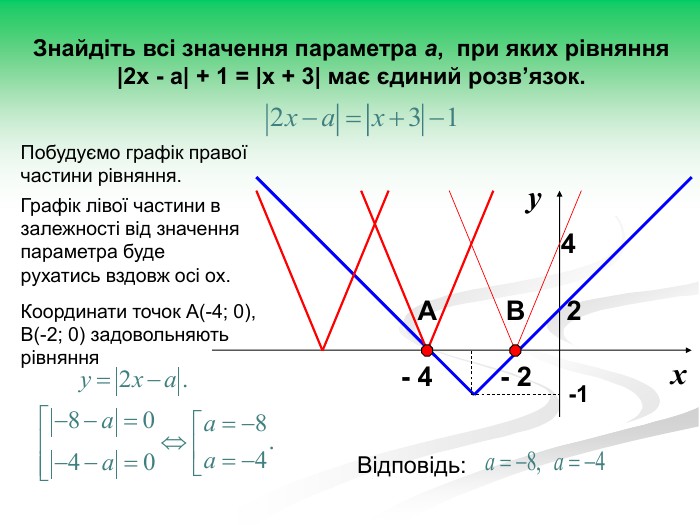
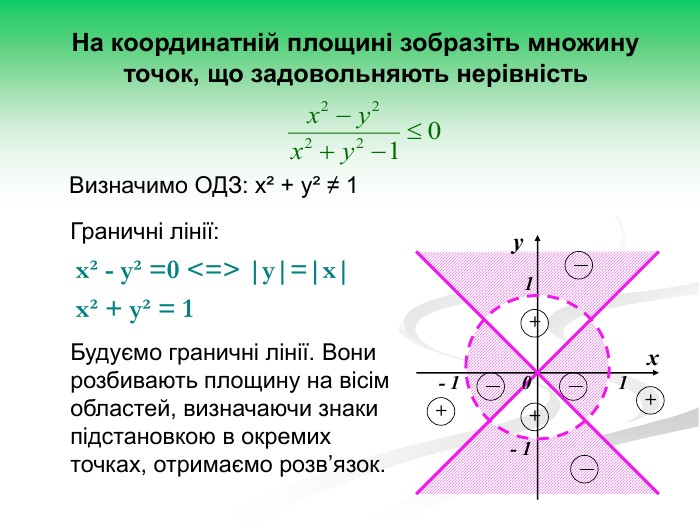
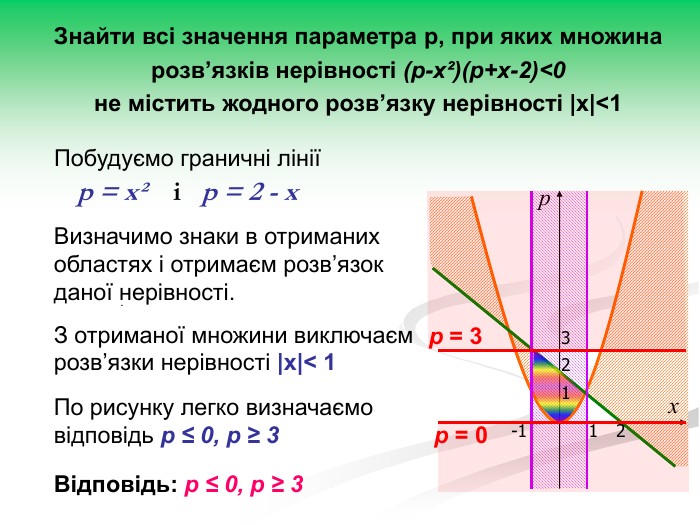
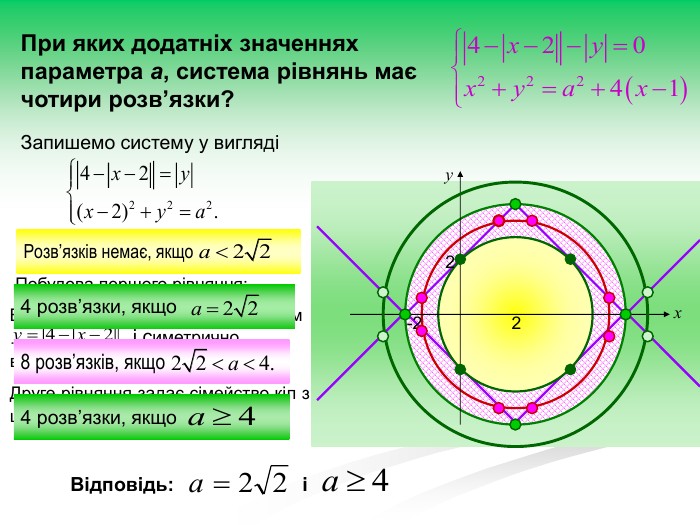
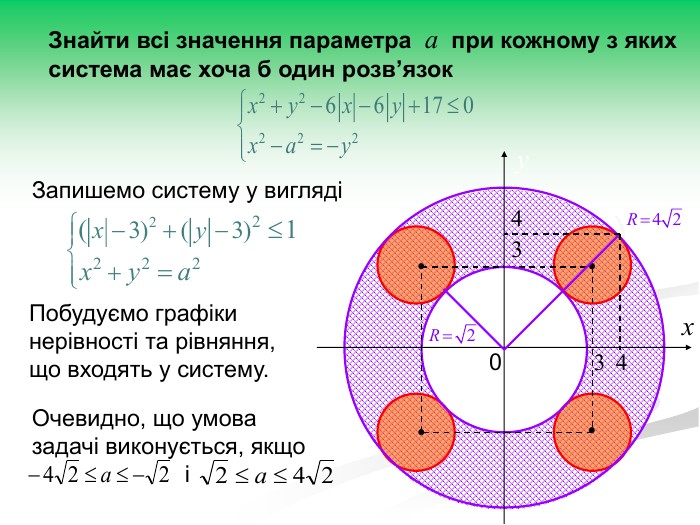
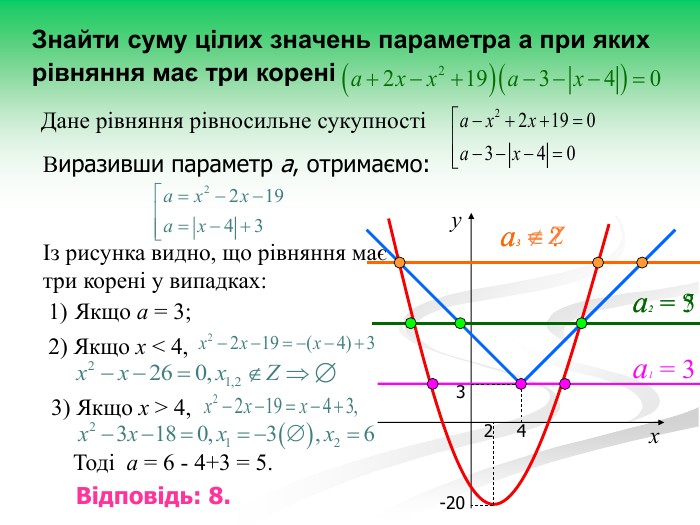
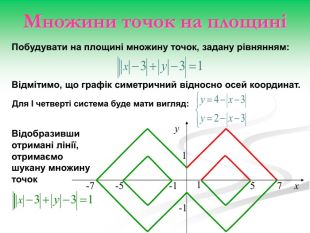
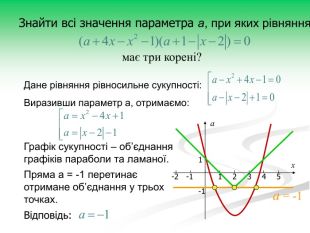
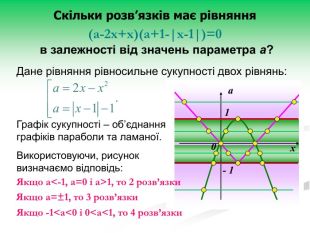
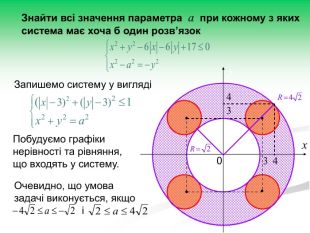
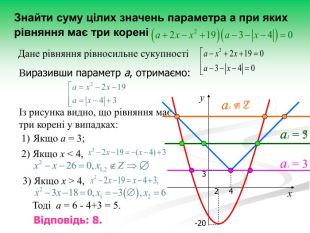
Рівняння та нерівності з параметрами
Про матеріал
Матеріал можна використати на уроках алгебри в 11 класі, а також для підготовки до ЗНО Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку