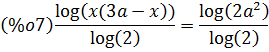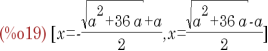Розв'язування логарифмічних рівнянь за допомогою пакету wx.Maxima
РОЗВ’ЯЗУВАННЯ ЛОГАРИФМІЧНИХ РІВНЯНЬ
ЗА ДОПОМОГОЮ ПАКЕТУ wxMaxima
Розв’язування задач з параметрами викликає в учнів певні трудності, оскільки ці завдання, як правило, пов'язані з дослідженням шуканих розв’язків в залежності від значень параметрів. Також, що рішення таких задач вимагає не тільки знання властивостей функцій та рівнянь, вміння виконувати алгебраїчні перетворення, але також високої логічної культурою і хорошої техніки дослідження.
Необхідною частиною вирішення подібних завдань є дослідження характеристики і кінцевого результату процесу в залежності від значень параметрів, причому, що рішення залежить не від кожного параметра в окремо, а від деякого їх характеристичного комплексу.
На основі застосування пакету wxMaxima, ми можемо так само вирішити заданя і побудувати графік рівняння.
Maxima - програма для виконання математичних обчислень,
символьних перетворень і побудови графіків. Система аналітичних обчислень Maxima ідеально підходить як для вивчення школярами старших класів, так і студентами, його можуть використовувати професійні математики для проведення складних розрахунків і досліджень.
Вирішуючи рівняння і нерівності з параметрами доцільно виконати рівносильні перетворення, так як перевірка може виявитися досить складним. Завдання, пов'язані з рішенням уравнний одержащих параметр, замінюється рівносильними.
Метою даної роботи є розгляд різних методів рішення логарифмічних рівнянь з параметрами за допомогою пакета wxMaxima
В даний час Maxima - це система комп'ютерної математики, яка призначена для виконання математичних розрахунків (як в символьній, так і в чисельному вигляді) таких як:
- Спрощення виразів;
- Графічна візуалізація обчислень;
- Рішення рівнянь і їх систем;
- Рішення звичайних диференціальних рівнянь та їх систем;
- Рішення задач лінійної алгебри;
- Рішення задач диференціального й інтегрального числення;
- Рішення задач теорії чисел і комбінаторних рівнянь і ін
У системі є велика кількість вбудованих команд і функцій, а також можливість створювати нові функції користувача. Система має свою власну мову. Вона також має вбудовану мову програмування високого рівня, що говорить про можливість вирішення нових завдань і можливості створення окремих модулів і підключення їх до системи для вирішення певного кола завдань.
Розглянемо рішення показникових і логарифмічних рівнянь з пара ¬ метром на конкретних прикладах.
Приклад 1
Знайти всі значення параметра a, при яких рівняння має єдиний корінь.
log 2 x + log 2 (3a-x) =2 log a+1
Розв’язання
log 2 x + log 2 (3a-x) =2 log a+1
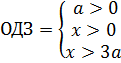
X (3a - x) = 2a2
3ax - x2 - 2a2 = 0
-x2 - 3ax - 2a2 = 0
х2 + 3ax + 2a2 = 0
x1 = 2a
x2 = a
Цей приклад ми розв’язали звичайним способом, а далі ми хочемо показати приклади,так як їх можна розв’язати за допомогою математичному пакеті wxMaxima
Приклад 2
log 2 x + log 2 (3a-x) =2 log a+1
|
Команда wxMaxima |
Результат wxMaxima |
|
Вводимо вихідне рівняння:
(%i6) eq1:2*Log(2, x) + Log(5,a+2) = |
|
|
Спрощуємо отриманий вираз: (%i7) logcontract((%o6)); |
|
|
Знаходимо корені: (%i8) solve([(%o7)], [x]); |
|
Приклад дослідження розв’язання (залежність кореня від параметра):
|
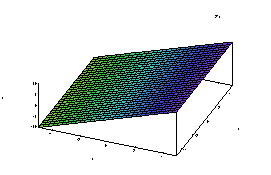
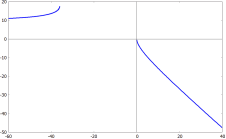
(%i25) plot2d([rhs((%o8)[1])], [a,-5,5], [plot_format, gnuplot]); |
(%i25) plot2d([rhs((%o8)[2])], [a,-5,5], [plot_format, gnuplot]); |
|
|
|
|
|
Пример 3.
log 5 x + log 5 (x+a) = log 5 a + 2log 5 3
|
Команда wxMaxima |
Результат wxMaxima |
|
Вводимо вихідне рівняння:
(%i17) eq1:Log(5, x) + Log(5,x+a) = |
|
|
Спрощуємо отриманий вираз: (%i18) logcontract((%o17)); |
|
|
Знаходимо корені: (%i19) solve([(%o18)], [x]); |
|
Приклад дослідження розв’язання (залежність кореня від параметра):
|
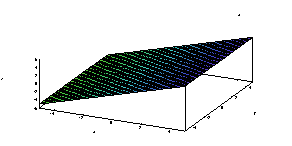
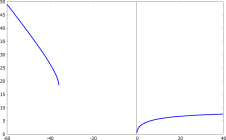
(%i28) plot2d([rhs((%o19)[1])], [a,-60,40], [plot_format, gnuplot]); |
(%i29) plot2d([rhs((%o19)[2])], [a,-60,40], [plot_format, gnuplot]); |
|
|
|
Література :
- Практикум з розв’язування задач з математики // За ред. В.І. Михайловського. – К.: Вища школа, 1989.
- Методичний посібник з вивчення математичного пакета wxMaxima

про публікацію авторської розробки
Додати розробку