Урок "Розв'язування рівнянь та систем рівнянь з параметром"

Тема уроку.  Розв’язування рівнянь та систем рівнянь з параметром (11 клас)

Мета уроку. Домагатися, щоб учні зрозуміли алгоритм розв’язування задач з параметром графічним способом. Виробляти уміння та навички розв’язувати рівняння та системи рівнянь з параметрами, використовуючи графічний спосіб. Розвивати мислення учнів,. Виховувати інтерес до математики, чіткість при виконанні малюнків.

Тип уроку. Урок вироблення умінь та навичок

План та хід уроку

1. Організаційний момент. Сьогодні ми проводимо звичайний урок алгебри та початків аналізу. Проте він трішки незвичайний. Його особливість у тому, що це – сотий урок в цьому навчальному році. А почнемо ми його традиційно: з перевірки домашнього завдання.
2. Перевірка домашнього завдання. Хто підготувався до уроку на високому рівні? Хто підготувався на достатньому рівні? Хто на середньому рівні ?
3. Повторення матеріалу про геометричні перетворення графіків функцій. Які геометричні перетворення потрібно виконати, щоб побудувати графіки функцій: , , , , , , , , ?

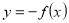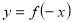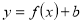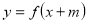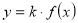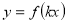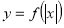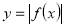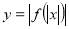• Робота в парах: встановити відповідність між функціями 1-4 і геометричними перетвореннями для побудови графіка функції А-Д.
• Усні вправи: що буде графіком вказаних функцій та рівнянь?

1) ,     2) ,     3) ,     4) ,   5) ,

6) ,   7) ,  8) ,     9) ,       10) ,

11) .

4. З’ясування нового навчального матеріалу.

 Учні вже ознайомлені, як розв’язувати рівняння з параметрами. Так ми вже розв’язували лінійні рівняння з параметром, квадратні, ірраціональні. Взагалі, задачі з параметрами – це досить цікава і звичайно нелегка тема. Вона має надзвичайно велике розвивальне значення. Адже при розв’язуванні задач з параметрами розвивається мислення, людина вчиться аналізувати, співставляти, розвивається уява, зорова пам'ять,  виховується уважність. Ця тема не містить теорем чи формул. І для того, щоб навчитися розв’язувати задачі з параметрами, (доречі, як ви вважаєте, як навчитися розв’язувати задачі з параметрами? – відповіді учнів) Щоб навчитися розв’язувати задачі з параметрами, треба їх розв’язувати !!!

В одній із письмових робіт вам було запропоновано завдання на високий рівень: визначити кількість коренів рівняння залежно від значення параметра а. Деякі учні успішно справилися із завданням.

Сьогодні ми навчимося розв’язувати рівняння та системи рівнянь використовуючи графічний спосіб.

Приклад 1. Знайти кількість коренів рівняння залежно від значень параметра а.

Щоб виконати це завдання, можна використати графічний спосіб.

Відповідь. а<0, немає коренів,

а=0, два корені,

0<a<3, чотири корені

 a=3, три корені

a>3, немає коренів.

Алгоритм розв’язування рівнянь з параметром графічним способом:

1. знайти область допустимих значень рівняння і параметра;
2. звести рівняння до вигляду 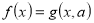, де функці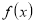ї і 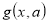такі, що їх графіки легко побудувати в координатній площині ху;
3. побудувати графіки функцій 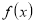і ;
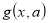4. розглядаючи всі можливі випадки розміщення цих графіків, дати відповідь на поставлене в задачі питання.

5. Закріплення матеріалу, розв’язування вправ

Приклад 2.  Знайти кількість коренів рівняння залежно від значень параметра а.

(учні виконують самостійно, можна усно)

Запитання до класу: чи можна було дані  завдання виконати ,не використовуючи графічний спосіб, тобто алгебраїчно? (очікувана відповідь: можна. Далі обговорюємо, як це зробити.

Приклад 3  .  Знайти кількість коренів рівняння залежно від значень параметра а.  ( учні виконують це завдання самостійно, робота в групах. По закінченні представник  групи коментує хід розв’язання, за сигналом вчителя представник іншої групи продовжує коментування. Відповідь перевіряємо: проектується  на екран)

Приклад 4. Знайти кількість розв’язків системи рівнянь

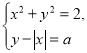залежно від значень параметра а.

(розв’язування проектується на екран)

Приклад 5. При яких значеннях параметра а система рівнянь

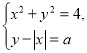має рівно два розв’язки ?

(розв’язування проектується на екран)

Приклад 6. Знайти кількість розв’язків системи рівнянь

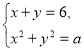залежно від значень параметра а.

(малюнок проектується на екран. Розв’язування – усно)

Приклад 7. Скільки розв’язків має система рівнянь

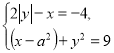залежно від параметра а?

(малюнок і детальне розв’язування – на екрані. На закріплення – слайд з рухомими графіками)

Приклад 8. Знайти всі значення параметра а, при кожному з яких рівняння

має рівно вісім розв’язків.

(малюнок, розв’язування та рухомі графіки проектуються на екран)

 Творче завдання: придумати рівняння або систему рівнянь з параметром (робота в групах). По закінченні виконання – обговорення завдань.

6. Підсумок уроку та завдання додому.

Вивчити алгоритм розв’язування рівнянь з параметром.

Вправа 1. При яких значеннях параметра а система рівнянь

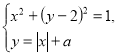має рівно три розв’язки ?

Вправа 2. Визначити кількість коренів рівняння  залежно від значень параметра а.