Робочий зошит до уроку "Конус та його елементи"

Для того, щоб дізнатися, над якою темою ми будемо працювати, нам необхідно розгадати наступний ребус

 

 

 

 

 

 

Робочий зошит

до вивчення теми: «___________»

учня (учениці) групи № ____

Козятинського МВПУ ЗТ

________________________________________

(Прізвище, ім’я)

 

 

Козятин – 20__

 

 

1. Повторення навчального матеріалу.

 Тест з теми «Циліндр».

1) Яка фігура є основою циліндра?

 а) Еліпс     б) Круг      в) Коло    г) Трикутник     

2) Чому дорівнює площа основи циліндра з радіусом 2см?

 а) 4π     б) 8π        в) 4         г) 2π

3) Як називається відрізок, виділений білим кольором?

а) діагональ циліндра                              

б) апофема циліндра

в) твірна циліндра

г) висота циліндра

 

4) Чому дорівнює площа осьового перерізу

циліндра,  радіус якого 1см  та твірна 3см?

      а) 6 см²

б) 3 см²

      в) 6π см²   

      г) 3π см²

5)  Площа перерізу, утвореного січною площиною,

перпендикулярною до осі циліндра, дорівнює 81π см² .

Чому дорівнює радіус циліндра?

а) 3 см

б) 9 см

в) 81 см

г) 6 см

	А	Б	В	Г
1
2
3
4
5

 

 

 

 

 

 

II. Сприйняття і усвідомлення нового навчального матеріалу.

1 Конус (Теоретичні відомості)

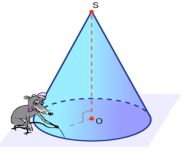
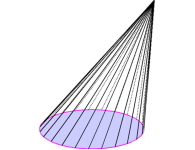
   ___________ конус _____________

 

 

 

 

 

 

3. Побудова конуса

                                                        Щоб отримати зображення конуса:

1. малюємо еліпс (зображення основи конуса),           відмічаємо його центр;

 2) з центра еліпса проводимо перпендикуляр,              

                                                              кінець якого є вершиною конуса;

 3) з вершини до еліпса проводимо дві контурні          твірні.

 

Побудуйте конус та позначте його елементи

 

 

 

 

4. Пошуковий практикум.

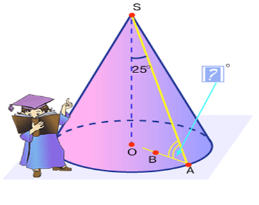                                                                      Чому дорівнює  кут між твірною  і основою конуса, якщо  відомо  кут між висотою і твірною.

 

_________________________________________

 

 

 

 

 

 

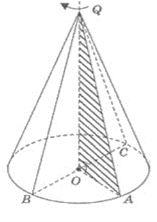5. Конус – тіло обертання (теоретичні відомості)

 

 

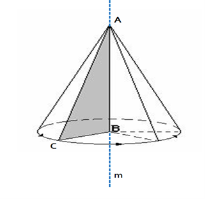
6.     Проблемне питання у процесі осмислення нового матеріалу.

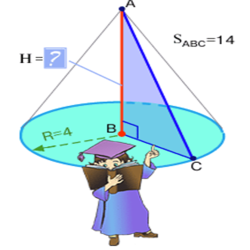Конус утворено при обертанні прямокутного трикутника S = 14 см2. Радіус основи конуса

4 см. Знайдіть висоту цього конуса.

 

 

 

 

 

7. Перерізи конуса площинами (теоретичні відомості)

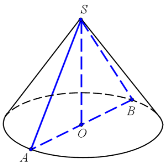
   ΔSAB –  осьовий переріз

 (_________________   трикутник).

 

 

 

 

 

 

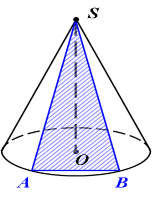
ΔSAB – переріз конуса площиною, яка походить через його вершину

ΔSAB – _________________, у якого бічні сторони є твірними конуса.

 

 

 

 

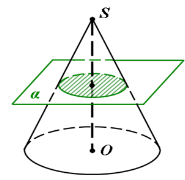
 Переріз конуса площиною, паралельною площині його основи є ____________ .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

8.    Пошуковий практикум

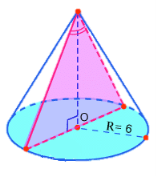
  Чому дорівнює площа осьового перерізу, якщо                    радіус основи конуса дорівнює 6 см, а твірна см?

 

 

 

9. Задача-тест                                          

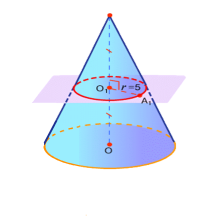
Через середину висоти конуса провели площину, яка перпендикулярна до осі конуса, та отримали круг r = 5 см. Чому дорівнює площа основи конуса?

       А)     25 π;

       Б)     10  π;

          В)     100  π;

       Г)     5 π;

       Д)     Інша відповідь.

 

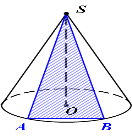10. Пошуковий практикум (додатково)

1.Переріз конуса площиною, що проходить через вершину, перетинає його основу по хорді довжиною 6см, яку видно з вершини під кутом 60°. Знайти площу утвореного перерізу.

 

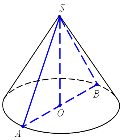
2. Осьовий переріз конуса – прямокутний трикутник. Знайдіть площу цього перерізу, якщо радіус основи 5 см.

 

 

 

ІІІ. Осмислення нового матеріалу.

11. Розв’яжіть кросворд:

1 .Фігура, утворена від обертання прямокутного трикутника навколо катета.                    

2. Перпендикуляр, опущений з вершини конуса на площину основи.

3. Відрізок, що сполучає вершину конуса з точкою кола.

 4. Переріз, що проходить через вісь конуса.

5. Вона сполучає вершину з центром прямого конуса.

6.Найвища точка конуса.

7 .Нижня частина конуса.

 

 

					1
				2
		3
			4
						5
6

 

 

 

ІV. Підсумок  уроку

12. Тест:

1. Конус – це тіло, утворене в результаті обертання…

А) Прямокутного трикутника навколо одного з катетів

Б) Прямокутного трикутника навколо гіпотенузи

В) Прямокутника навколо однієї з його сторін

Г)Трикутника навколо однієї зі сторін

Д) Правильного трикутника навколо однієї зі сторін

 

2. Якщо SB і SK – твірні конуса, то вони…

А) Мимобіжні

Б) Перпендикулярні

В) Паралельні

Г) Перетинаються

Д) Інша відповідь

 

3.  Переріз конуса площиною, що проходить через його вершину є…

А) Кругом

Б) Півкругом

В) Рівнобедреним трикутником

Г) Прямокутником

Д) Рівностороннім трикутником

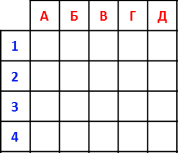
4. Який переріз конуса, що проходить через його вершину, має найбільшу площу…

 

А) Круг

Б) Осьовий переріз

В) Рівнобедрений трикутник

Г) Прямокутний трикутник

Д) Рівносторонній трикутник

 

 

 

 

 

 

 

 

V. Релаксація, самооцінка та оцінка викладача.

Твій настрій:

                                    

                       САМООЦІНКА:                ОЦІНКА ВЧИТЕЛЯ:

 

 

VI. Домашнє завдання.

Підручник під редакцією О. С. Істера «Математика: (алгебра і початки аналізу та геометрія, рівень стандарт)» для 11 класу, задачі №№ 6.4, 6.12, 6.17.

Творче завдання:   Реферат з елементами дослідження: «Конуси навколо нас чи ми навколо конусів».