1

«ВСТУП. Що вивчає геометрія?»

         Правило

    Шкільний курс геометрії традиційно поділяють на планіметрію та стереометрію. Планіметрія    вивчає фігури на площині, стереометрія — фігури в просторі.        Приклади

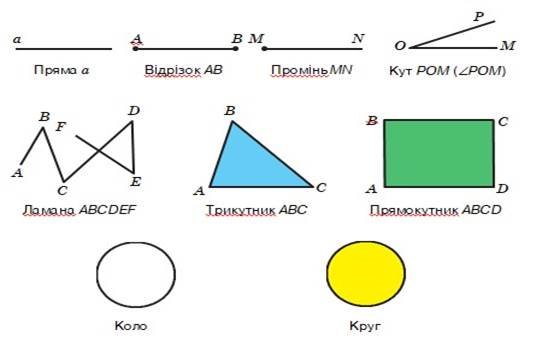
Так, усі геометричні фігури, зображені на рисунку  вам добре відомі.

            

                 Розв’яжи самостійно

                         Познач та дай назву зображеним геометричним фігурам.

 

                                         

 

 

 

 

                Корекційна картка № 2       «Точки та прямі»

             Правило

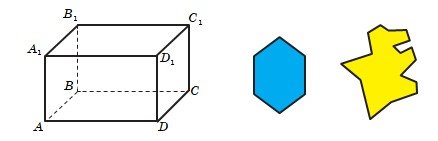
Шкільний курс геометрії традиційно поділяють на планіметрію та стереометрію. Планіметрія    вивчає фігури на площині, стереометрія — фігури в просторі. Точка — найпростіша геометрична фігура. Говорять, що точка A належить прямій a, або точка A лежить на прямій a, або пряма a проходить через точку А Основна властивість прямої. 

  Через будь-які дві точки можна провести пряму, і до того ж тільки одну.

    Означення.                                                                                                                                               

Дві прямі, які мають спільну точку, нази-вають такими, що перетинаються.

Теорема 1.1.                                                                                                                                       

Будь-які дві прямі, що перетинаються, мають тільки одну спільну точку.

         Приклади

              

                    

                      Розв’яжи самостійно

1.     буквою m.Позначте точки A і B, які лежать на цій прямій, і точки C, D, E, які не лежать на ній.

 

2.     Проведіть прямі a і b так, щоб вони перетиналися. По-значте точку їхнього перетину буквою C. Чи належить точка C прямій a? прямій b?

 

 

 

3.     Позначте чотири точки, жодні три з яких не лежать на одній прямій.

 

 

 

 

3

«Відрізок і його довжина»

                  Правило

Для будь-яких двох точок існує єдиний відрізок, для якого ці точки є кінцями,

тобто відрізок своїми кінцями задається однозначно.                                                          

Означення. Два відрізки називають рівними, якщо їх можна сумістити накладанням. Для її вимірювання треба вибрати одиничний відрізок. Залежно від вибору одиниці довжини змінюється числове значення довжини відрізка.

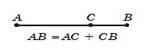
Основна властивість довжини відрізка. Якщо точка C є внутрішньою точкою відрізка AB, то відрізок AB дорівнює сумі відрізків AC і CB  тобто AB AC + CB.

         Означення. Серединою відрізка AB називають таку його точку C, що AC = CB.          Приклади

                  1.     2.        

3.  AB = 17 мм, або AB = 1,7 см, або AB = 0,17 дм тощо.

4.        5.      

                    Розв’яжи самостійно

1.     Яка з точок,позначених на рисунку,лежить між двома іншими? Запишіть відповідну рівність, що випливає з основної властивості довжини відрізка.

 __________________________________________________________

_____                     

                               А               М                   Р

2.     Точка М — внутрішня точка відрізка АР. Знайдіть:  АР, якщо АМ =1,8 дм, МР=2,6 дм;

      2) довжину відрізка АM,якщо АР= 42 мм, АМ= 1,5 см.

Корекційна картка №4

«Промінь. Кут. Вимірювання кутів»

                  Правило

Означення. Два промені, які мають спільний початок і лежать на одній прямій, називають доповняльними.

Означення. Кут, сторонами якого є доповняльні про-мені, називають розгорнутим.

Означення. Два кути називають рівними, якщо їх можна сумістити     накладанням.

Означення. Бісектрисою кута називають промінь з початком у вершині кута, який ділить цей кут на два рівних кути.

Означення. Кут, градусна міра якого дорівнює 90°, називають прямим. Кут, градусна міра якого менша від 90°, називають гострим. Кут,градусна міра яьшаза90°, але менша від 180°, називають тупим.

Основна властивість величини кута. Якщо про-мінь OC ділить кут AOB на два кути AOC і COB, то AOB = AOC + COB

       Приклади                                                                                   

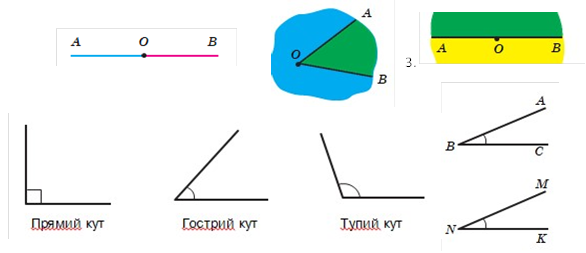                                              4.                     .                                                                                                   

                           

                           

Розв’яжи самостійно

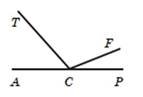Із вершини розгорнутого кута ACP проведено два промені CT і CF так, що ACF 158, TCP 134. Знайдіть кут TCF.

 

                                   

5

«Суміжні та вертикальні кути»

         Правило

Означення. Дві прямі називають перпендикулярними, якщо при їхньому перетині утворився прямий кут.

Означення. Два відрізки називають перпендикулярними, якщо вони лежать на перпендикулярних прямих.

Теорема 5.1.Через кожну точку прямої можна провести пряму, перпендикулярну до даної, і до того жтільки одну

         Приклади

      1.                       

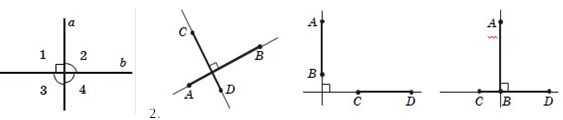
Записують: ABCD.

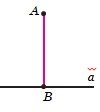У такому випадку говорять,що з точки A напряму  aопущено перпендикуляр AB. Точку B називають основою перпендикуляра AB.

Довжину перпендикуляра AB називають відстанню від точки A до прямої a.  

                      Розв’яжи самостійно

 1.Проведіть пряму c і позначте на ній точку K. Користуючись косинцем, проведіть через точку K пряму, перпендикулярну до прямої c.

 

 

2. Накресліть кут ABK, який дорівнює: 1) 73; 2) 146. Позначте на промені BK точку C і проведіть через неї прямі, перпендикулярні до прямих AB і BK.

 

 

 

6

« Рівні трикутники. Висота, медіана, бісектриса трикутника»

          Правило

Означення. Периметром трикутника називають суму довжин усіх його сторін.               Периметр позначають буквою P.

Означення. Трикутник називають гострокутним, якщо всі його кути гострі.

Трикутник називають прямокутним, якщо один із його кутів прямий. Трикутник

називають тупокутним, якщо один із його кутів тупий.                                                        

Означення.  Дватрикутникиназиваютьрівними,якщо їх можна сумістити накладанням. Означення. Перпендикуляр,опущений з вершини трикутника напряму,яка містить протилежну сторону, називають          висотою трикутника.            Означення.Відрізок,який сполучає вершину трикутника із серединою

протилежної сторони,називають медіаною трикутника.                                              Означення. Відрізок бісектриси кута трикутника, який сполучає вершину трикутника з точкою протилежної сторони, називають бісектрисою трикутника.

Приклади

 

           Розв’яжи самостійно

1.     Накресліть довільний трикутник і проведіть усі його медіани.

 

2.     Накресліть довільний трикутник і проведіть усі його бісектриси

 

3.     Одна зі сторін трикутника в 5 разів менша від другої та на 25 см менша від              третьої. Знайдіть сторони три-кутника, якщо його периметр дорівнює 74 см.

7

«Перша  ознака рівності трикутників» Правило

Теорема (перша ознака рівності трикутників: за двома сторонами та кутом між ними). Якщо дві сторони та кут між ними одного трикутника дорівнюють відповідно двом сторонам та куту між ними другого трикутника, то такі трикутники рівні.                      Означення.Пряму,яка перпендикулярна до відрізка та проходить через його середину, називають серединним перпендикуляром відрізка.                                                         Теорема Кожна точка серединного перпендикуляра відрізка рівновіддалена  від кінців цього відрізка

         Приклади

 

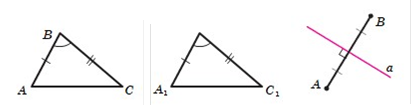
                    Розв’яжи самостійно

1.За допомогою лінійки та транспортира побудуйте трикутник,дві сторони якого дорівнюють 3см і 6см,а кут між ними — 40.

 

            

 

 

 

 

 

 

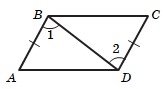              2. На рисунку ABCD, 12, AD 7 см, C 34.                             

Знайдіть відрізок BC і кут A.

 

8

« Друга ознака рівності трикутників»

 

Теорема (друга ознака рівності трикут-ників: за стороною та двома прилеглими до неї кутами). Якщо сторона та два прилеглих до неї кути одного трикутника дорівнюють відповідно стороні та двом прилеглим до неї кутам другого трикутника, то такі трикутники рівні.

 

         Приклади

 

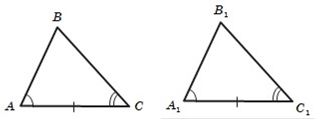
                    Розв’яжи самостійно

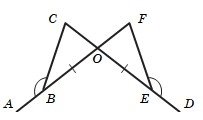
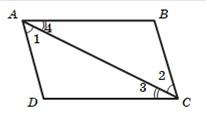         На рисунку ABC DEF, BO OE.                                              

Доведіть, що BCO EFO.

 

 

               На рисунку   ABC DEF, BO OE.                                      

Доведіть, що BCO EFO.

 

 

 

 

 

 

9

«Рівнобедрений трикутник та його властивості» Правило

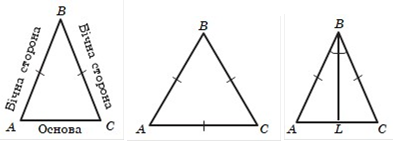
Означення. Трикутник, у якого дві сторони рівні,називають рівнобедреним.

Рівні сторони  рівнобедреного трикутника називають бічними сторонами, а третю сторону — основою рівнобедреного трикутника.

Означення. Трикутник, у якого всі сторони рівні,називають рівностороннім.

Теорема (властивості рівнобедреного трикутника).                                                                      

У рівнобедреному трикутнику:  1) кути при основі рівні;  2)бісектриса трикутника,проведена до його основи, є медіаною та висотою трикутника. Із теореми  випливає, що:

1) у трикутнику проти рівних сторін лежать рівні кути;2) у рівнобедреному трикутнику бісектриса, висота й медіана, проведені до його основи, збігаються;

3) у рівносторонньому трикутнику всі кути рівні;4) у рівносторонньому трикутнику  бісектриса,висота й медіана, проведені з однієї   вершини, збігаються.;                                                                              

         Приклади

 

                    Розв’яжи самостійно

1)Знайдіть периметр рівнобедреного трикутника, основа якого дорівнює  13 см, а бічна сторона — 8 см.

 

 

2)Периметр рівнобедреного трикутника дорівнює 39см, а основа —15см.Знайдіть бічні сторони трикутника.

 

10

«Ознаки рівнобедреного трикутника»

 

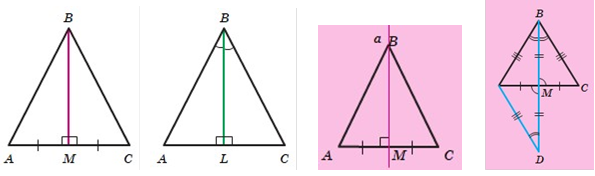
Теорема  Якщо медіана трикутника є його висотою, то цей трикутник рівнобедрений.

Теорема  Якщо бісектриса трикутника є його висотою, то цей трикутник    рівнобедрений.

Теорема  Якщо в трикутнику два кути рівні, то цей трикутник рівнобедрений.

    Теорема Якщо медіана трикутника є його бісектрисою, то цей трикутник рівнобедрений          Приклади

 

                    Розв’яжи самостійно

      1.У трикутнику ABC медіана BK перпендикулярна до сторони AC.                                    

Знайдіть кут ABC, якщо ABK 25.

 

 

 

 

 

       2.Серединний перпендикуляр сторони AC трикутника ABC проходить через вершину B. Знайдіть кут C, якщо A 17.

 

 

 

 

       3.УтрикутникуABCвідомо,що ACB90, A B45, CK — висота.                                     

Знайдіть сторону AB, якщо CK 7 см.

 

11

«Третя ознака рівності трикутників»

 

Теорема (третя ознака рівності трикутників: за трьома сторонами).                                        Якщо три сторони одного трикутника дорівнюють відповідно трьом сторонам другого трикутника, то такі трикутники рівні.

Теорема  Якщо точка рівновіддалена від кінців відрізка, то вона належить серединному перпендикуляру цього відрізка.

 

        Приклади

 

 

                    Розв’яжи самостійно

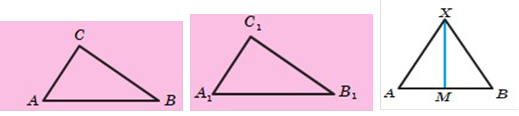
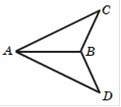На рисунку  AC AD, BC BD.                                                                 

Знайдіть кут BAC, якщо BAD 25.

 

 

 

 

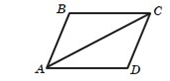 На рисунку ABCD, BC AD.

Доведіть, що B D.

 

 

 

 

12

«Паралельні прямі»

 

Означення. Дві прямі називають паралельними, якщо вони не перетинаються.

 Теорема (ознака паралельності прямих) Дві прямі,які перпендикулярні до третьої  прямої,паралельні.   Наслідок. Через дану точку M, яка не належить прямій a, можна провести пряму b, паралельну прямій a. Основна властивість паралельних прямих (аксі-ома паралельності прямих).Черезточку,яка не лежить на даній прямій, проходить тільки одна пряма, паралельна даній.                                                                                  

Теорема  Якщо дві прямі паралельнітретій прямій, то вони паралельні.

                                                                              

         Приклади

 

                    Розв’яжи самостійно

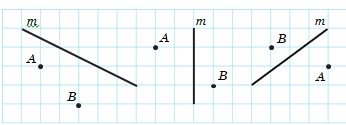            Перерисуйте в зошит рисунок .

Проведіть через кожну з точок A

і B пряму, паралельну прямій m.

 

 

 

 

 

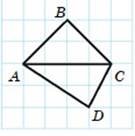 Перерисуйте в зошит рисунок. Проведіть через точку B пряму

m, паралельну прямій AC, а через точку D — пряму n, паралельну прямій AC. Яке взаємне розміщення прямих m і n?

 

 

13

«Ознаки паралельності двох прямих»

                  Правило

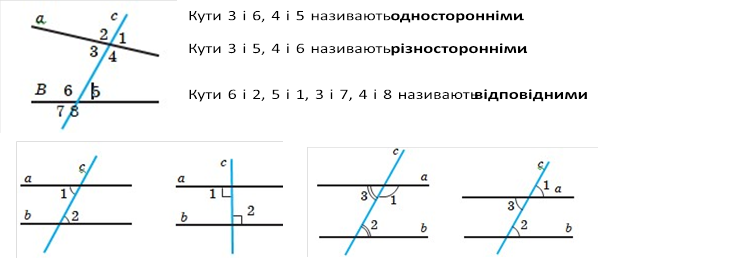
Якщо дві прямі a і b перетнути третьою прямою c, то утвориться вісім кутів. Пряму c називають січною прямих a і b.

      Теорема Якщо різносторонні кути,утворені при перетині двох прямих січною,                        рівні,  то прямі паралельні.

Теорема  Якщо сума односторонніх кутів, утворених при перетині двох прямих січною,дорівнює180,то прямі паралельні.

       Теорема  Якщо відповідні кути, утворені при перетині двох прямих січною,                            рівні, то прямі паралельні.

         Приклади

 

                    Розв’яжи самостійно

1. На яких із рисунків  а–г прямі a і b паралельні?

 

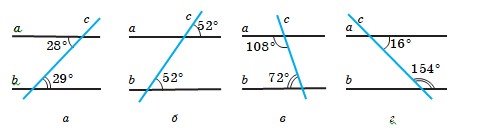
                                                                          Запишіть, які прямі на рисунку  є паралельними, якщо                      

153, 2128, 3127.

14

«Властивості паралельних прямих»

                  Правило

Теорема 15.1 (обернена ).Якщо дві паралельні прямі перетинаються січною, то кути, які утворюють пару різносторонніх кутів,рівні.

Теорема 15.2 (обернена ). Якщо дві паралельні прямі перетинаютьсясічною,токути,якіутво рюють пару відповідних кутів, рівні.

Теорема 15.3 (обернена ). Якщо дві паралельні прямі перетинаються січною, то сума кутів, які утворюють пару односторонніх кутів, дорівнює 180.

Наслідок. Якщо пряма перпендикулярна до однієї з двох паралельних прямих,то вона перпендикулярна й до другої .                                                                                                         

Означення. Відстанню між двома паралельними прямими називають відстань від будь-якої точки однієї з прямих до другої прямої.

         Приклади

 

                    Розв’яжи самостійно

1. 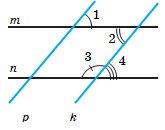             На рисунку  m II n, p II k, 150.                                     Знайдіть кути 2, 3 і 4.

 

 

 

 

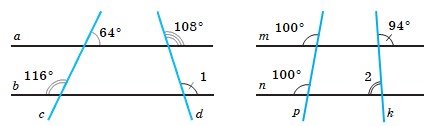
2.              На рисунку 1 знайдіть кут 1. На рисунку 2 знайдіть кут 2.

 

 

15

«Сума кутів трикутника. Нерівність трикутника» Правило

Теорема  Сума кутів трикутника дорівнює 180.

Означення. Зовнішнім кутом трикутника називають кут, суміжний із кутом                            цього трикутника.

Теорема  Зовнішній кут трикутника дорівнює сумі двох кутів трикутника,                                не суміжних з ним.

Наслідок. Зовнішній кут трикутника більший за кожний із кутів трикутника,                           не суміжних з ним.

     Теорема (нерівність трикутника).Кожна сторона трикутника менша від суми двох інших його сторін.

Теорема  У трикутнику проти більшої сторони лежить більший кут, і навпаки, проти більшого кута лежить більша сторона.

         Приклади

 

                    Розв’яжи самостійно

1.Знайдіть кут трикутника, якщо два інших його кути дорівнюють 35і 96.

 

          2.Знайдіть кути при основі рівнобедреного трикутника, якщо кут при вершині дорівнює 104.

 

 

 

          3.У трикутнику ABC відомо, що C 90, AK — бісек-триса, BAK 18.                               

Знайдіть кути AKC і ABC.

 

 

Корекційна картка № 16

«Прямокутний трикутник»

                  Правило

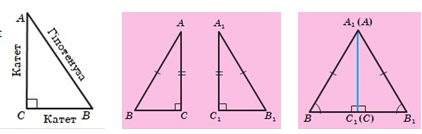
              Сторону прямокутного трикутника, протилежну прямому куту,називають  гіпотенузою,а сторони,прилеглі до прямого кута, — катетами

Теорема  (ознака рівності прямокутних трикутників за гіпотенузою та катетом).       Якщо гіпотенуза та катет одного прямокутного трикутника відповідно дорівнюють гіпотенузі та катету другого, то такі трикутники рівні.

Ознака рівності прямокутних трикутників за двома катетами. Якщо катети одного         прямокутного        трикутникавідповіднодорівнюютькатетамдругого,то            такі трикутники рівні.

Ознака рівності прямокутних трикутників за катетом і прилеглим гострим кутом. Якщо катет і прилеглий до нього гострий кут одного прямокутного трикутника відповідно дорівнюють катету й прилеглому до нього гострому куту другого, то такі трикутники рівні.

Ознака рівності прямокутних трикутників за катетом і протилежним гострим кутом. Якщо катет і протилежний йому гострий кут одного прямокутного трикутника відповідно дорівнюють катету й протилежному йому гострому куту другого, то такі трикутники рівні.

Ознака рівності прямокутних трикутників за гіпотенузою та гострим кутом.            Якщо гіпотенуза та гострий кут одного прямокутного трикутника відповідно дорівнюють гіпотенузі та гострому куту другого, то такі трикутники рівні.

         Приклади

                     

                    Розв’яжи самостійно

         1.Один із гострих кутів прямокутного трикутника до-рівнює 43.              

Знайдіть другий гострий кут.

 

         2.У рівнобедреному трикутнику ABC (ABBC) проведено висоту AH.

Знайдіть кут CAH, якщо B76.

17

«Властивості прямокутного трикутника»

 

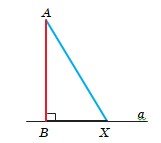
     Теорема   У прямокутному трикутнику гіпотенуза більша за катет.

Наслідок. Якщо з однієї точки, яка не лежить на прямій, до цієї прямої проведено перпендикуляр і похилу, то перпендикуляр менший від похилої.

 

         Приклади

                      

                    Розв’яжи самостійно

Сторони прямокутного трикутника дорівнюють 24 см, 10 см і 26 см.               

Чому дорівнює найбільший катет даного трикутника?

 

 

 

 

        2.У прямокутному трикутнику DEF гіпотенуза DE до-рівнює 18 см, D 30.    Знайдіть катет FE.

 

 

 

 

У прямокутному трикутнику MKC відомо, що M 90, C 60, CM 7 см.   Знайдіть гіпотенузу CK.

 

 

 

18

«Геометричне місце точок. Коло та круг»

                  Правило

Означення. Геометричним місцем точок (ГМТ) називають множину всіх точок,                     які   мають певну властивість.

Теорема   Серединний перпендикуляр відрізка є геометричним місцем точок, рівновіддалених від кінців цього відрізка.

Пряма теорема. Кожна точка серединного перпендикуляра відрізка рівновіддалена від його кінців.

Обернена теорема. Якщо точка рівновіддалена від кінців відрізка, то вона належить   серединному перпендикуляру цього відрізка.

Теорема   Бісектриса кута є геометричним місцем точок, які належать куту й рівновіддалені від його сторін.

Пряма теорема. Кожна точка бісектриси кута рівновіддалена від його сторін.

Обернена теорема. Якщо точка,що належить куту, рівновіддалена від його сторін, то вона лежить на бісектрисі цього кута.

Означення. Колом називають геометричне місце точок, відстані від яких до заданої точки дорівнюють даному додатному числу.

Означення. Кру́гом називають геометричне місце точок, відстані від яких до заданої точки не більші за дане додатне число.

         Приклади

 

                    Розв’яжи самостійно

1.                 Відрізки MK і EF — діаметри кола із центром O, MK 12 см, ME10см.    Знайдіть периметр трикутника FOK.

 

2.                 Відрізки AC і AB — відповідно діаметрі хорда кола із центром O, BAC 26               Знайдіть кут BOC.

 

19

«Властивості кола. Дотична до кола»

 

Теорема  Діаметр кола, перпендикулярний до хорди, ділить цю хорду навпіл.

Теорема  Діаметр кола, який ділить хорду, від-мінну від діаметра, навпіл, перпендикулярний до цієї хорди.

Означення. Пряму,яка має з колом тільки одну спільну точку, називають дотичною до кола.

Теорема  (властивість дотичної). Дотична до кола перпендикулярна до радіуса, проведеного в точку дотику.

Теорема (ознака дотичної до кола).Якщо пряма, яка проходить через точку кола, перпендикулярна до радіуса, проведеного вцю точку, то ця пряма єдотичною до даного кола.

Наслідок. Якщо відстань від центра кола до деякої прямої дорівнює радіусу кола, то ця пряма є дотичною до даного кола.

         Приклади

 

                    Розв’яжи самостійно

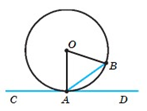1.Пряма CD дотикається до кола із центром O в точці A, відрізокAB —хорда кола,BAD35Знайдіть кут AOB.

 

            

2. Дано коло, діаметр якого дорівнює 6 см. Пряма a від-далена від його центра:

1)на2см;2)на3см;3)на6см. У якому випадку пряма a є дотичною до кола?

20

«Описане та вписане кола трикутника»

 

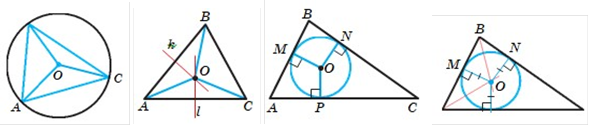
Означення. Коло називають описаним навколо трикутника, якщо воно проходить через усі його вершини.

Теорема  Навколо будь якого трикутника можнаописати коло.

Наслідок 1. Три серединних перпендикуляри сторін трикутника перетинаються в одній точці.

Наслідок 2. Центр кола, описаного навколо трикутника, — це точка перетину серединних перпендикулярів сторін трикутника.

Означення. Коло називають вписаним у трикутник, якщо воно дотикається до всіх його сторін.

Теорема   У будь який трикутник можнавписати коло.

Наслідок 1. Бісектриси кутів трикутникаперетинаються в одній точці.

Наслідок 2. Центр кола, вписаного в трикутник,— це точка перетину бісектрис трикутника.

         Приклади

 

                    Розв’яжи самостійно

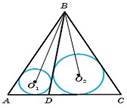На рисунку  у трикутники ABD і CBD вписано кола із центрами О₁ і О₂ відповідно, ABC 50. Знайдіть кут O₁BO₂.

 

 

 

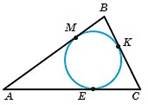2.Коло,вписане в трикутник ABC дотикається до його сторін у

точках M, K і E, AB13 см, BC 8 см, BK 3 см.                                  

Знайдіть сторону AC.

 

21

«Задачі на побудову»

 

Під задачею на побудову розуміють вимогу:побудувати за допомогою інструментів геометричну фігуру, яка б задовольняла певній заданій умови.

Розв'язати задачу на побудову — означає:

1.     знайти послідовність елементарних  побудов, після виконання  яких  шукана  фігура вважається  побудованою;

2.     довести, що саме ця фігура задовольняє умову задачі.          Приклади

1.Побудувати кут що дорівнює даному.

 

               Розв’яжи самостійно

1.Накресліть: 1) гострий кут; 2) тупий кут. Побудуйте кут, що дорівнює накресленому.

 

 

22

«Задачі на побудову»   Правило

Розв'язати задачу на побудову — означає:

1.знайти послідовність елементарних  побудов, після виконання  яких  шукана  фігура вважається  побудованою;

2.довести, що саме ця фігура задовольняє умову задачі.

 Приклади

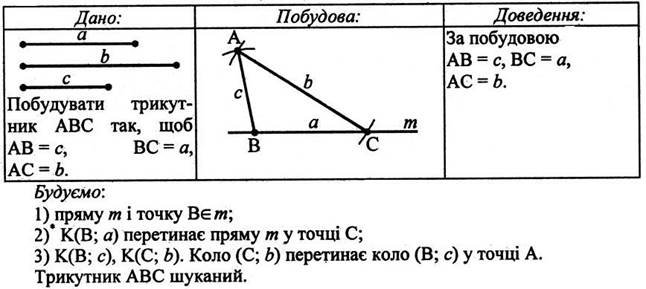
2.Побудувати трикутник за трьома сторонами

 

                    Розв’яжи самостійно

             Побудуйте трикутник:

1)     за двома сторонами та кутом між ними;

 

 

 

 

2)     за стороною та двома прилеглими кутами.

 

 

 

Корекційна картка № 23

«Задачі на побудову»

                  Правило

Розв'язати задачу на побудову — означає:

1.знайти послідовність елементарних  побудов, після виконання  яких  шукана  фігура вважається  побудованою;

2.довести, що саме ця фігура задовольняє умову задачі.          Приклади

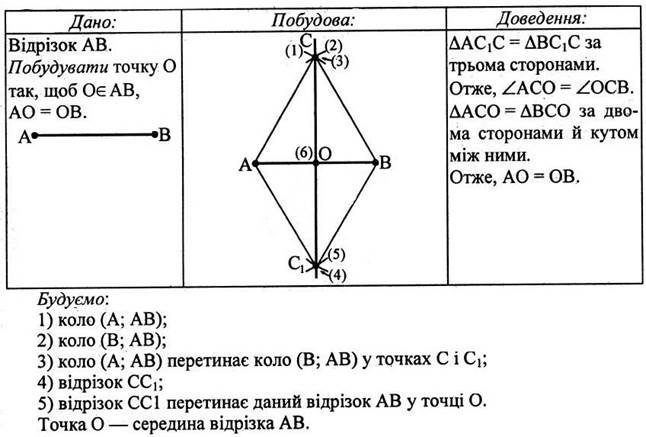
3. Поділити відрізок навпіл.

 

Розв’яжи самостійно

1.Поділіть даний відрізок на чотири рівні частини.

 

 

Корекційна картка № 24

«Задачі на побудову» Правило

Розв'язати задачу на побудову — означає:

1.знайти послідовність елементарних  побудов, після виконання  яких  шукана  фігура вважається  побудованою;

2.довести, що саме ця фігура задовольняє умову задачі.          Приклади

4.Побудувати пряму, перпендикулярну   до даної.

 

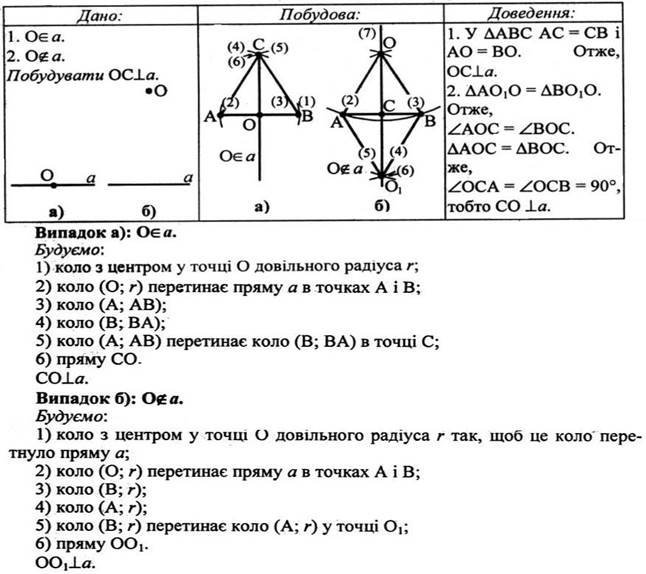
Розв’яжи самостійно

1.Побудуйте дотичну до кола, яка проходить через дану точку кола.