Робота МАН "Методи доведення нерівностей"

Міністерство освіти і науки

Департамент освіти і науки Полтавської облдержадміністрації

Полтавське територіальне відділення МАН України

Новосанжарське районне наукове товариство учнів «Мала академія наук»

Відділення: фізико-математичне та економічне

Секція: математика

МЕТОДИ ДОВЕДЕННЯ НЕРІВНОСТЕЙ

Роботу виконала:

Степаненко Ірина Віталіївна,

учениця 11 класу

Малокобелячківської

загальноосвітньої школи І-ІІІ ступенів         Новосанжарської районної ради

Науковий керівник:

Тимощук Ніна Олексіївна,

учитель математики

Малокобелячківської

загальноосвітньої школи І-ІІІ ступенів Новосанжарської районної ради,

спеціаліст вищої кваліфікаційної категорії, старший вчитель

ТЕЗИ

науково-дослідницької роботи

«Методи доведення нерівностей»

Автор: Степаненко Ірина Віталіївна, учениця 11 класу Малокобелячківської загальноосвітньої школи І-ІІІ ступенів

Новосанжарської районної ради Полтавської області

Науковий керівник: Тимощук Ніна Олексіївна, учитель математики Малокобелячківської ЗОШ І-ІІІ ступенів, спеціаліст вищої кваліфікаційної категорії, старший вчитель

Полтавське територіальне відділення МАН України

секція: математика

 Доведення нерівностей викликає у багатьох учнів певні труднощі. Доведення більшості нерівностей вимагає знання різноманітних теоретичних відомостей, застосування різних теорем та формул.

Актуальність даної роботи полягає в тому, що доведення нерівностей викликає у багатьох учнів певні труднощі.

Мета роботи: розглянути різні методи доведення нерівностей.

Реалізація поставленої мети передбачає виконання таких завдань: проаналізувати методичну літературу з означеної теми;  ознайомитись з теоретичними відомостями, що стосуються даної теми;  розглянути різноманітні методи доведення нерівностей; навести приклади на доведення нерівностей; показати практичне застосування методів доведення нерівностей.

Об’єкт дослідження – нерівності.

Практична значимість: дана  робота може бути використана вчителями та учнями на уроках при вивченні теми “Доведення нерівностей”, на факультативних заняттях, заняттях гуртка.

Опрацювавши літературу, розглянувши різноманітні методи доведення нерівностей ми  зробили  висновок: отримати навички доведення нерівностей можна лише тоді, коли розв’язати їх достатню кількість, ознайомившись з різними методами та прийомами доведення.

ЗМІСТ

ВСТУП…………………………………………………………………………..4

РОЗДІЛ 1. НЕРІВНОСТІ В МАТЕМАТИЦІ…….……………….................. 5

1.                     Історичні відомості про виникнення нерівностей……………5
2.                     Основні відомості про нерівності……………...………………5
   1.           Основні поняття………………………….…………........5
   2.           Властивості числових нерівностей…..…………………6
   3.           Перетворення нерівностей…..………………………….6

РОЗДІЛ 2. ДОВЕДЕННЯ НЕРІВНОСТЕЙ………………………….….…..8

1.                     Класичні нерівності……………………………………...……..8
2.                     Методи доведення нерівностей………………...………………9
   1.             Метод від супротивного……………………………........9
   2.             Синтетичний метод…………………………………….10
   3.             Аналітичний метод……………..……………………….11
   4.             Аналітико-синтетичний метод………………..……….12
   5.             Метод математичної індукції…………………..………12
   6.             Метод рівносильних перетворень……………………..14

3.                     Деякі прийоми для доведення нерівностей……..…………...16   
   1.      Застосування похідної……………………….. ..……….16
   2.      Монотонність площ і об’ємів….……………….………16

РОЗДІЛ 3. ПРАКТИЧНЕ ЗАСТОСУВАННЯ МЕТОДІВ ДОВЕДЕННЯ НЕРІВНОСТЕЙ……….………………………………………………....….....…...18

ВИСНОВКИ………………………………………………………….………..19

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ…………………………………….21

ДОДАТКИ……………………………………………………………………..23

ВСТУП

Тема нашої роботи «Методи доведення нерівностей». Ми вибрали цю тему тому, що доведення нерівностей відіграють важливу роль у розвитку логічного мислення і служить основою формування математичних знань і вмінь.

Актуальність даної роботи полягає у тому, що доведення нерівностей викликає у багатьох учнів певні труднощі. Доведення більшості нерівностей вимагає знання різноманітних теоретичних відомостей, застосування різних теорем та формул. Отримати навички доведення нерівностей можна лише тоді, коли розв’язати достатньо велику кількість, ознайомившись з різними методами та прийомами розв’язання.

Мета даної роботи в тому, щоб розглянути різні методи доведення нерівностей.

 Для досягнення поставленої мети необхідно:

1.     опрацювати методичну літературу з означеної теми;
2.     ознайомитись з теоретичними відомостями, що стосуються даної теми;
3.     розглянути різноманітні методи доведення нерівностей;
4.     навести приклади доведення нерівностей;
5.     показати практичне застосування методів доведення нерівностей.

Відповідно до поставлених завдань використані такі методи дослідження: аналітичний; синтетичний; математичної індукції; доведення від супротивного; монотонності.

Об’єкт дослідження – нерівності.

Практична значимість даної роботи в тому, що оскільки доведення нерівностей викликає в учнів позитивні емоції, розриває їх математичну індукцію на кмітливість, то даний матеріал можна вивчати на факультативних заняттях та спецкурсах, на заняттях математичного гуртка, при підготовці до ЗНО.

РОЗДІЛ 1

НЕРІВНОСТІ В МАТЕМАТИЦІ

1.                Історичні відомості про виникнення нерівностей

Як відомо, виникнення чисел обумовлено проблемами практичної діяльності людини. Застосування ж чисел вимагало вміння їх порівнювати. Робити це люди навчились багато тисячоліть тому.

Ще в “Началах” Евкліда суто геометрично було обґрунтовано нерівність , де розглядали як довжини відрізків. [1, 47]

З розвитком математики без порівняння величин, без поняття “більше” і “менше” не можна було дійти до поняття рівності, тотожності, рівняння. Наближені обчислення (в тому числі і обчислення …) пов’язані з поняттям рівності. [2, 13]

Знаки нерівності “<” і “>”, які використовуються і в наш час, вперше ввів англійський математик Томас Гаррітон  у своїй роботі “Практика аналітичного мислення”.  Його книжка, де він використовував ці знаки, побачила світ у 1631 році. “Гаррітон обґрунтував своє нововведення так: якщо дві величини не дорівнюють одна одній, то відрізки, що фігурують у співвідношенні, не паралельні, а перетинаються. Перетин може бути справа (<) і зліва (>). У друкарнях використовували для нерівностей букву V, що вже була відома в ті часи, бо відповідного знака для набору не мали”.

Знаки нестрогих нерівностей  “≤” та “≥”… були введені  в 1734 році французьким математиком П’єром Буге. Спочатку їх записували по-іншому, але з часом знаки нестрогих нерівностей набули сучасного вигляду.

1.                Основні відомості про нерівності

1.               Основні поняття

Нерівність – відношення, яке зв’язує два числа a₁ і a₂ за допомогою … знаків: < (менше), ≤ (менше або дорівнює), > (більше), ≥ (більше або дорівнює),

≠ ( не дорівнює), тобто а₁ < а₂, а_{1 ≤} а_2,, а_{1 >}  а₂, а_{1 ≥} а₂, а₁ ≠ а₂. [4, 410]

Нерівності розглядають числові та буквені. Якщо нерівність виконується при всіх значеннях змінних, то вона називається тотожною нерівністю.

Нерівність зазивають алгебраїчною, якщо зі змінними виконують алгебраїчні дії. Решту нерівностей називають неалгебраїчними, або трансцендентними.

2.               Властивості числових нерівностей

Існують різні способи доведення нерівностей, проте в основі кожного з них лежать ті чи інші основні властивості числових нерівностей, які вивчаються в шкільному курсі математики або безпосередньо випливають з них. Всі вони є наслідками такої сукупності нерівностей:

1.        якщо а > b, то b < а; якщо а < b, то b > a;
2.        якщо а > b, та b >с, то а > с;
3.        якщо а > b, то а + с > b + c;
4.        якщо а > b та с -- додатне число (с > 0), то ас > bc;
5.        якщо а < b і с – від’ємне число (с > 0), то ас > bc.
6.        якщо а > b і c > d, то а + с > b + d;
7.        якщо а, b, c, d – додатні числа, причому а > b і с > b, то  ас> bd;
8.        якщо а > b і с < d, то а - с > b - d;
9.        якщо а > b > 0, то   <  ;
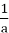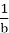10.   якщо а > b > 0, то для будь-якого натурального числа n виконується нерівність аⁿ > bⁿ. [5, 44]

3.               Перетворення нерівностей

Під час розв’язування та доведення нерівностей виконують перетворення аналогічні до перетворень рівнянь.

1. Нерівності f(x) < g(x) i g(x) > f(x) рівносильні.
2. Нерівності f(x) < g(x) і f(x) – g (x) < 0 рівносильні.
3. Якщо функція f(x) визначена на всій області визначення нерівності

f(x) < g(x), то нерівність f(x) + g(x)  <  g(x) + f(x) рівносильна даній.

4. Нерівність f(x) < g(x) є наслідком нерівності f(x) + g(x)  <  g(x) + f(x).
5. Якщо φ(х)  > 0 при всіх значеннях змінної з області визначення нерівності f(x) < g(x), то нерівність f(x) φ(x) < g(x) φ(х) рівносильна даній.
6. Нерівності 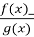>0 i f(x) g(x) > 0 рівносильні.
7. Якщо функції f(x) і g(x) невід’ємні на деякій множині, то на цій множині нерівності f(x) < g(x) і (f(x))ⁿ < (g(x))ⁿ, n є N, рівносильні.
8. Нерівності <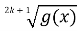, k є N, i f(x) < g(x) рівносильні.
9. Нерівності (f(x))^2k < (g(x))^2k , k є N, і < рівносильні.
10.  Нерівність f(x) < g(x) є наслідком нерівності < 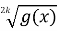, k є N;
11. Якщо g(x) набуває тільки невід’ємних значень, то нерівність f(x) < 0 є наслідком нерівності 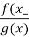< 0. [6, 42]

Дві нерівності з однією змінною х називається рівносильними, якщо множина розв’язків цих нерівностей  співпадає. [7, 69]

РОЗДІЛ 2

ДОВЕДЕННЯ НЕРІВНОСТЕЙ

Існують такі задачі, в яких крім нерівності задається деяка множина значень змінних і потрібно довести, що всі її елементи належать множині розв’язків даної нерівності. Такі задачі прийнято називати задачами на доведення нерівностей.

Якщо в задачі на доведення нерівностей про множину значень змінної нічого не сказано – це означає, що нерівність потрібно довести для всіх дійсних значень змінної. [8, 74]

Довести – це означає показати, що ця нерівність виводиться з відомих або очевидних тверджень. При цьому часто використовують різні допоміжні співвідношення. Мабуть, найбільш популярна в цій ролі нерівність а² + b² ≥ 2ab, де а і b – довільні числа. [9, 37]

Доводять ті нерівності, які є висловленнями. Загального методу доведення нерівностей не існує. Щоб довести нерівність A > B, де А і В – числа, досить показати, що А - В --  число додатне. Якщо А і В – вирази із змінними, то, щоб довести, що при заданій множині значень цих змінних А > В, досить показати, що для кожного з цих значень різниця А - В має додатне  значення. [10, 87]

Під час доведення нерівностей використовують: загальні методи доведення математичних тверджень, спеціальні способи і штучні прийоми.

1.                Класичні нерівності

Найбільш відомим нерівностями, до яких вдаються під час доведення, є:

1.        нерівність Коші (співвідношення між середнім арифметичним і середнім геометричним)

  ≥

де – невід’ємні дійсні числа; знак рівності має місце тоді й тільки тоді, коли

2.        нерівність Коші-Буняковського

 ()² ≤ • ,

де , k=1, … , n, -- довільні дійсні числа; коли = λ, k=1, …, n. [11, 191]

3.        нерівність трикутника

≤ +  ,

де , , k=1, …, n, -- довільні числа; знак рівності має місце тоді й тільки тоді, коли =  , k=1, …, n. [11, 192]

4.        yзагальнена нерівність Коші

≥ ,

де , … ,, α₁, … , α_n – невід’ємні дійсні числа; знак рівності має місце тоді й тільки тоді, коли , =… = . [11, 193]

2.                Методи доведення нерівностей
   1.             Метод від супротивного

Один із методів, який широко застосовується для доведення тверджень, є метод доведення від супротивного. Припустивши протилежну нерівність правильною, виконують перетворення, поки не дійдуть до висновку, що результат суперечить умові.

Наприклад. Довести, якщо ≥ 0, ≥ 0, то ≤.

Доведення

Припустимо протилежне. Нехай існує набір невід’ємних чисел , для яких дана нерівність хибка, тобто істинна нерівність

>.

Ліва і права частини цієї нерівності невід’ємні. Піднесемо їх до квадрата, матимемо:

;

^;

;

< 0;

< 0;

< 0;

< 0

Остання нерівність хибна, оскільки сума квадратів не може бути від’ємним числом. Одержана суперечність указує на те, що зроблене припущення хибне, а тому нерівність

> для ≥ 0, ≥ 0, ≥ 0 - правильна. [12, 19]

2.             Синтетичний метод

Суть методу полягає в тому,  що з допомогою відомих властивостей і деяких відомих опорних нерівностей кількома перетвореннями встановлюють нерівність, яку потрібно довести. Такими опорними нерівностями можуть бути, наприклад, нерівності, які можна вважати загальновідомими. По іншому можна сказати, що синтетичний метод доведення полягає в тому, що, рухаючись від даних, виводять те, що потрібно довести як логічний висновок.  Наприклад, шляхом системних міркувань можна провести доведення такої нерівності: , > 0.

Доведення

Якщо > 0 і ≥ 0, то

Маємо або , звідки отримаємо , що й потрібно було довести. Під час доведення цим методом часто виникають утруднення у виборі вихідних даних і нерівностей, що слідують з них. Щоб правильно зробити проміжні висновки, потрібно весь час пам’ятати, що саме треба довести.

Приклад. Довести, що    ≥  , коли = 1.

Доведення

Виберемо як опорні такі два істинні твердження:

= =1,

= ≥ 1.

Рівність =1  і нерівність ≥ 0  можна почленно додати, зберігаючи знак нерівності. Одержимо ≥ 1. Розділивши обидві частини нерівності на 2 матимемо: ≥ . Далі міркуємо аналогічно:

  =   ≥ ;

= ≥ 0.

Додамо почленно останні нерівності:

 ≥  ,

 ≥  ,

що й потрібно було довести.

3.             Аналітичний метод

Це один з найпоширеніших методів. Його суть полягає в тому, що для доведення нерівності оцінюють різницю між лівою та правою її частинами, тобто користуються означенням.

Доведемо нерівність Коші для випадку n = 2 аналітичним методом.

≥ ,  якщо   ≥ 0, ≥ 0,  -  ≥  0;

  ≥ 0; ≥ 0.

Оскільки очевидно, що ( - )² ≥ 0,  то    ≥  .

Приклад 1. Довести, що  ≥ .

Доведення

Домножимо ліву і праву частину нерівності на 2 і знайдемо їх різницю:

 ≥ 0 або

≥ 0.

Останнє очевидно. Рівність буде тільки при [13, 131]

4.             Аналітико-синтетичний метод

Найчастіше використовується аналітико-синтетичний метод. Доведення проводять і через знаходження достатніх умов для висновку (аналітично), і шляхом розгортання умови (синтетично). Аналіз – метод відшукування доведення, синтез – метод викладу доведення.

Приклад. Довести нерівність ≤ 1

Доведення

Проведемо аналіз. Нерівність дістане красиву геометричну, а точніше тригонометричну, інтеграцію, якщо в цьому виразі   закінчити на sin α, а на sin β… множина значень співпадає з множиною значень sin α; аналогічно, множина значень    співпадає з множиною значень sin β. Нерівність набуває вигляду:

≤ 1.

Або |sin α | cos β| +sin β| sin α|| ≤1, що рівносильна нерівності |sin (α ± β)| ≤1,  а це відомий факт. Виконуючи перетворення, зворотні проведеним під час аналізу, дістанемо доведення нерівності. [14, 69]

5.             Метод математичної індукції

Метод математичної індукції ґрунтується на так званому принципі математичної індукції, що є різновидом аксіом індукції (однієї з аксіом формальної теорії натуральних чисел). Його можна сформулювати так: якщо твердження  А(n), де n – натуральне число істинне для n =1,  і з того , що воно істинне для n =k , де k – будь-яке натуральне число, випливає його істинність для наступного числа n=k+1, то твердження А(n) істинне для будь-якого натурального числа n.

Доведення методом математичної індукції складається з трьох частин:

1.     Доводимо (перевіряємо) істинність твердження А(1).
2.     Припустимо, що А(n) істина для n=k, і доводимо істинність цього твердження для n=k+1, тобто доводимо справедливість теореми A(k) →A(k + 1).
3. На основі принципу математичної індукції робимо висновок, що твердження істинне для будь-якого натурального n. [14, 69]

Доведемо нерівність Беркуллі ≥ 1 + na, а > -1, n є N методом математичної індукції.

1.        n = 1:      1 + а ≥ 1 + а – істинне.
2.        Припустимо, що нерівність істинна для n = k:         (1 + а)^k ≥ 1 + ka.

Доведемо істинність нерівності Беркуллі для n = k + 1, тобто істинність

(1 + а)^k+1 ≥ 1 + (k + 1) a

(1 + a)^k+1=(1 + a)(1 + a)^k ≥(1+ а )(1 + ak) = 1 + a(k + 1) + a²k> 1 + a(k + 1)

Отже, нерівність виконується і при n = k + 1. За принципом математичної індукції це означає, що твердження правильне для всіх натуральних значень n.

Приклад. Довести, що • • …• < , де n – натуральне число. [15, 22]

Доведемо задану нерівність методом математичної індукції.

а) При n = 1 нерівність набирає вигляду < . Отже, при n = 1 задана нерівність справджується.

б) Припустимо, що нерівність справедлива при n = k, тобто

• • • …  < .

Доведемо, що нерівність буде справедливою при n = k + 1, тобто

• • • … • • <  .

Для цього досить довести нерівність:

• < ., або   < .

Знайдемо різницю:   -  = > 0

Отже , > , що й треба було довести.

6.             Метод рівносильних перетворень

Іноді нерівність досить легко можна довести виконуючіи рівносильні перетворення, які дають там очевидну нерівність. Доведення багатьох нерівностей зводиться до виконання тотожних перетворень заданих виразів і застосування основних властивостей нерівностей, у результаті чого дістають очевидні нерівності. До найбільш поширених прийомів, які використовуються при тотожних перетвореннях, належать:

а) підсилення або мажоризація нерівності;

б) побудова ланцюжка правильних нерівностей, які потім почленно додаються або перемножаються;

в) заміна змінної у відомій нерівності (цей прийом називають ще спеціалізацією нерівності);

г) використання відомих тотожностей.

У будь-якому випадку необхідно уважно стежити за тим, щоб на кожному кроці ми одержували рівносильні нерівності: тільки за цієї умови можна стверджувати, що остання в ланцюжку проведених тотожних перетворень очевидна нерівність рівносильна  початковій, тобто ми дійсно довели шукане твердження.  Це зауваження слід пам’ятати під час використання будь-яких методів доведення. Проілюструємо на прикладах цей спосіб доведення нерівностей. [16, 4]

Приклад (Підсилення нерівностей). Довести нерівність >

Доведення.

Маємо: - + - +…+ = ( - ) + ( - ) + … + ( - ) + > - ) +

+ ( - ) = + = > . Ми врахували, що кожна дужка суми додатна. [16, 5]

Приклад. Довести нерівність 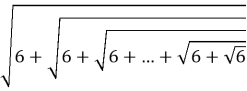< 3 за умови, що ліва  її частина містить будь-яку скінченну кількість радикалів.

Доведення

Замінимо під знаком останнього внутрішнього радикала число 6 на 9. В одержаному в такий спосіб виразі всі корені послідовно добуваються та його значення дорівнює 3. Але ліва частина даної в умові нерівності менша за значення одержаного виразу. Отже, дана в умові нерівність справедлива.[17, 20]

Приклад (використання відомої нерівності). Довести нерівність:

(a + b)(b + c)(a +c) ≥ 8abc при а ≥ 0, b ≥ 0 і с ≥ 0. [18, 93]

Доведення

Використовуючи відому нерівність ≥ при а ≥ 0 і b ≥ 0, маємо:

 a + b ≥ 2; b + c ≥ 2 a +c ≥ 2. Перемножимо почленно отримані нерівності: (a + b)(b + c)(a +c) ≥ 2 •2 •2.

(a + b)(b + c)(a +c)  ≥ 8 = 8. Враховуючи, що a ≥ 0, b ≥ 0, c ≥ 0

(a + b)(b + c)(a +c) ≥ 8abc. Нерівність доведено.

Приклад (різниця лівої та правої частини). Довести нерівність:

a²b² + a² + b² +4 ≥  6 ab

Доведення

Розв’язуючи нерівності з використанням різниці лівої та правої частини маємо змогу довести, що ця різниця набуває значень постійного знака при будь-яких значеннях змінних.

a²b² + a² + b² +4 - 6 ab = a²b²- 4ab + 4 + a²- 2ab + b²= (ab-2)² + (a –b)²

При будь-яких значеннях а і b ця різниця набуває тільки невід’ємних значень, отже, нерівність, що доводиться, є правильною. [19, 129]

3.                Деякі прийоми для доведення нерівностей
   1.             Застосування похідної

Щоб довести нерівність виду (х) > g(x) (або (х) < g(x)) за допомогою похідної використовують схему:

1.               Розглянути допоміжну функцію f(x) =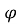(x) – g(x) (на її області визначення або на заданому проміжку).
2.               Дослідити за допомогою похідної поведінку функції f(x) (зростання чи спадання або її найбільше чи найменше значення) на розглянутому проміжку.
3.               Обґрунтувати (спираючись на поведінку функції f(x)), що f(x) > 0 (або f (x) < 0) на розглянутому проміжку, і зробити висновок, що (x) > g(x) (або (x) < g(x)) на цьому проміжку.

Приклад. Довести, що sin х < х для всіх х > 0.

Доведення

Розглянемо функція f(x) = x – sin x. f'(x) = 1 – cosx ≥ 0 для всіх

х є R. Отже, f(x) зростає на R. Якщо х>0, то f(x)> f(0), тобто x – sin x>0 або sin x < x.

Нерівність доведено.

2.             Монотонність площ і об’ємів

Нехай просторову фігуру F розбито на дві прості фігури F₁ i F₂, а S(F),

S (F₁), S(F₂) – їх площі.  Оскільки за означенням площі простої фігури площа --  величина додатна і S(F)=S(F₁)+S(F₂), то S(F₁)< S(F), тобто площа простої фігури F₁, яка є складовою частиною простої фігури F , менша за площу самої фігури. Цю властивість називають мононністю площ і коротко записують так: якщо F₁ F, то S(F₁) S(F). Таку ж властивість мають і об’єми простих тіл: якщо Т₁, Т – прості тіла і Т₁ Т, то V(Т₁₎ < V(Т). [11, 209]

Приклад. Довести нерівність.

(a + c) (b + d) ≤  +

Доведення

Побудуємо прямокутник ABCD, у якого сторона AB = + с, сторона ВС = = b + d, і впишемо в нього чотирикутник KLMN. (Точки K, L, M, N відповідно належать сторонам AB, BC, CD, AD.  АK = , КВ = с, ВL = b,  LС = d, СМ = с, МD = , ND = b, АN = d.)  Очевидно, що

(a + c)(b +d)= S_ABCD = 2S_KLMN = 2(S_KLM + S_LMN) =

KN•KLsinK + MN•LM•sinM ≤  KN•KL+ MN•LM =

+.

Нерівність доведено.

В роботі були вже показані такі прийоми доведення нерівностей: за означенням, за властивостями квадратного тричлена; посилення нерівності зведення до очевидних або відомих нерівностей.

РОЗДІЛ 3

ПРАКТИЧНЕ ЗАСТОСУВАННЯ МЕТОДІВ ДОВЕДЕННЯ НЕРІВНОСТЕЙ

Задача 1. Довести, що опір послідовного з’єднання n провідників перевищує опір паралельного з’єднання тим же провідників не менше, ніж в n² раз.

Доведення

Позначимо опір даних провідників, через r₁, r₂, …, r_n. Нехай R- опір послідовного з’єднання, а R₁— опір паралельного з’єднання провідників. Тоді,

R =  + r_2+…+ r_n;  = + + … + .

Тоді = (r₁ + r₂ + … + r_n )( + + … + ).

За теоремою про середнє арифметичне можемо записати

r₁ + r_2+…+ r_n  ≥ n,  + + … + ≥ n,

звідки маємо ≥ n², що і треба було довести. [8, 76]

Задача 2. У вигляді якої фігури потрібно збудувати клітку для лева, щоб вона мала найбільший об’єм?

Розв’язання

Позначимо довжину, ширину і висоту клітки a, b, c. Тоді довжина всих ребер фігури m=4(a+b+c), за умовою об’єм V=abc повинен бути найбільшим. Оскільки x³ + y³ + z³ ≥ 3xyz, то вважаючи, що x³ = а, y³ = b,  z³ = c, маємо a+b+c ≥ 3. Тоді abc ≤ (a+b+c)³=

Рівність можлива, коли a=b=c. У цьому випадку об’єм буде найбільшим. Тому клітка повинна мати форму куба, довжина ребра якого знаходимо з рівняння x³= . Звідки х =.

Відповідь: клітка має мати форму куба.

ВИСНОВОК

Опрацювавши літературу про доведення нерівностей, ми отримали такі висновки.

Мистецтвом доводити нерівності оволодіти досить нелегко. Тут необхідний чималий досвід, інтуїція і вміння вільно застосовувати різні технічні прийоми.

Майстерність доводити нерівності ґрунтується на володінні високим рівнем знань теоретичної частини курсу та певним арсеналом методів і прийомів доведення нерівностей.

Загального методу доведення нерівностей не існує, але існує чимало спеціальних методів  (див. Додаток А), з допомогою яких вдається довести значну кількість нерівностей. Тому доцільно ознайомитися з різноманітними методами та прийомами доведення нерівностей, які ми розглянули в роботі.

Загальні методи доведення: 1) від супротивного; 2) синтетичний; 3)аналітичний; 4) аналітико-синтетичний; 5) метод математичної індукції; 6)рівносильних перетворень;

Спеціальні прийоми: 1) за означенням числової нерівності; 2) посилення та послаблення; 3) за властивостями квадратного тричлена; 4) зведення до очевидних або відомих нерівностей; 5) побудова ланцюжка правильних нерівностей; 6) заміна змінної; 7) застосування похідної; 8) використання тотожності площ і об’ємів; 9) оцінювання розв’язків.

Знання методів і прийомів доведення нерівностей дозволить, здавалося б, складні нерівності доводити просто, зрозуміло і красиво, а сформовані уміння і навички знадобляться при розв’язанні вправ на доведення.

Для чого потрібно вміти доводити нерівності? Для того, щоб за їх допомогою розв’язувати задачі. Уміння доводити нерівності дозволить учням використовувати уміння та навички при розв’язанні  раціональних, ірраціональних, логарифмічних, показникових та тригонометричних нерівностей.

Дана робота має на меті допомогти читачеві навчитися доводити нерівності, а також знаходити раціональні методи доведення.

Дуже важливо постійно здобувати нові знання і не зупинятися на тому, що вже знаємо. Доведення нерівностей сприяє розвитку логічного мислення, творчого підходу в розв’язуванні не лише математичних, а й життєвих проблем.

Матеріали, наведені у цій роботі, можуть бути корисні як учителям при вивченні доведення нерівностей, при організації заключних повторень курсу з математики за програмою основної школи, так і старшокласникам під час підготовки до олімпіад та ЗНО.

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1.                   Кравчук В. Алгебра: Підручник 9 класу/  Кравчук Василь, Підручна Марія, Янченко Галина — Тернопіль: Підручники і посібники, 2009 – 256 с.
2.               Глейзер Г.И., История математики в школе VII-VIII кл. Пособие для учителей / Г.И.Глейзер — Просвещение, 1982. – 240с.
3.               www.scribd.com/doc/12089683/06- Лінгвістичне походження базової математичної лексики. Про походження деяких математичних знаків.
4.               Математический энциклопедический словарь/ Гл.ред. Ю.В.Прохоров;  ред. кол.:  С.И.Адян, Н.С.Бахвалов,  В.И.Битюцков,  А.П.Ершов, Л.Д.Кудрявцев, А. Л. Онищик, А.П.Юшкевич – М. : Сов. энциклопедия, 1988. – 847 с., ил.
5.                   Чекова А.М. Алгебра і початки аналізу в таблицях. 7-11 класи. Навчальний посібник / А. М. Чекова. — Х. : Науково-методичний центр, 2003. –248 с.
6.               Математика: посібник для факультативних занять, 9 кл. / Л.М.Вивальнюк, О.І Соколенко,  В.Н . Боровик та інші — К. :Освіта, 1993. – 176 с.
7.               Мордкович А.Г. Алгебра и начала анализа: Учебное пособие для подготовительных отделений вузов./  А.Г.Мордкович — М. : Высшая школа, 1979. – 399с.
8.               Пособие по математике для поступающих в вузы. За ред. Г.Н. Яковлева (А.Д. Кутасов, Т.С. Пиголкина, В. И. Чехлов, Т. Х. Яковлева — М. : Наука 1985. – 480с.
9.               Обласні математичні олімпіади (І.М.Конет, В.Г.Паньков, В.М.Радченко, Ю. В. Теплінський — Кам’янець-Подільський: Абетка,  2000. — 304 с.
10.          Бевз Г. П. Довідник з математики/  Г.П. Бевз – К. : Радянська школа, 1981. – 262с.
11.          Вороний  О.М. Готуємось до олімпіад з математики/  О.М. Вороний – Х.: Вид. група «Основа», 2009. – 255 с.
12.          Швець В. О. Доведення числових нерівностей. / В.О.Швець, Л.В.Заболотний//  Математика – 2002 – №35 – с.15-22.
13.          Баранов И. А. Математика для подготовительных курсов техникумов/  И.А. Баранов,  Г. И. Богатырев,  О.А.Боковнев – М: Наука, 1983. – 336с.
14.          Рижков М.О. Матеріали  для факультативних занять, спецкурсів, гуртків. Математика 8-11/  М.О. Рижков – Х.: Вид. група «Основа», 2008. – 96с. — (Б-ка журн. «Математика в школах України», Вип. 9(69)).
15.          Горделедзе Ш.Г. Збірник конкурсних занять з математики/ Ш.Г.Горделедзе,  М. Ш. Кухарчук,  Ф. П. Яремчук  – К.:  Вища школа, 1974. –322 с.
16.          Семенов В.О.  Доведення нерівностей.  Числові послідовності:  скінченні суми і добутки. Книга 2/ О.В. Семенов – Х.: Вид. група «Основа», 2009. – 176с. –(Б-ка журн. «Математика в школах України», Вип. 7(79)).
17.          Мороз О.Л. Доведення числових нерівностей. Добірка вправ/ О.Л.Мороз//  Математика — 2002. – №36 – с.19-22.
18.          Нагибін Ф.Ф. Математическая шкатулка:  Пособие для учащихся 4-8 кл. сред. шк./ Ф.Ф.Нагибин, Е.С.Канин — 5-е издание – М.: Просвещение, 1988. – 160с.: ил.
19.          Гайштут  О.Г.  Математика: довідник для абітурієнтів та учнів загальноосвітніх навчальних закладів/  О.Г. Гайштут,  Ф.Т. Умаков,  А.О.Шамович — К.: Літера ЛТД. 2012. – 624с.
20.          Саакян  С.М.  Задачи по алгебре и началам анализа для 10-11 классов/  С.М. Саакян,  А.М.Гальдман,  Д.В.Денисов — М.: Просвещение, 1990. –– 256с.: ил. – (Б-ка учителя математики).

ДОДАТОК А