Урок з математики на тему: «Логарифмічні рівняння та логарифмічні нерівності»

Про матеріал

Конспект відкритого заняття Тема: "Логарифмічні рівняння та логарифмічні нерівності" Цілі дидактичні:  актуалізувати знання про логарифмування та потенціювання;  забезпечити узагальнення і систематизацію знань з теми;  формувати вміння розв’язувати логарифмічні рівняння та нерівності. розвиваючі:  розвивати логічне мислення, математичну мову;  розвивати алгоритмічну, інформаційну та графічну культуру;  розвивати аналітичні здібності, пам’ять, увагу, інтуїцію студентів;  розвивати мотиваційну сферу особистості;  розвивати зацікавленість студентів при розв’язуванні задач прикладного характеру. виховні:  сприяти вихованню наполегливості при розв’язуванні задач;  сприяти вихованню культури взаємовідносин при роботі в парах, групах, колективі. Тип заняття: узагальнення і систематизація знань Обладнання: плакат з властивостями логарифмів, таблиця оцінювання навчальних досягнень студентів, таблиця набраних балів командами під час змагання, емблеми команд, мультимедійна система. Роздатковий матеріал: картки для конкурсу «Перевір себе», картки для конкурсу капітанів, картки для конкурсу «Відгадай слово». Очікуванні результати: студенти повинні вміти застосовувати набуті знання при розв’язуванні логарифмічних рівнянь та нерівностей.

Перегляд файлу

ВІДКРИТЕ ЗАНЯТТЯ з навчальної дисципліни «Математика»

на тему: «Логарифмічні рівняння та логарифмічні нерівності»

Викладач Тіунова О.І.

Конспект відкритого заняття

Тема Логарифмічні рівняння та логарифмічні нерівності Цілі дидактичні:

§ актуалізувати знання про логарифмування та потенціювання;

§ забезпечити узагальнення і систематизацію знань з теми;

§ формувати вміння розв’язувати логарифмічні рівняння та нерівності.

розвиваючі:

§ розвивати логічне мислення, математичну мову;

§ розвивати алгоритмічну, інформаційну та графічну культуру;

§ розвивати аналітичні здібності, пам’ять, увагу, інтуїцію студентів;

§ розвивати мотиваційну сферу особистості;

§ розвивати зацікавленість студентів при розв’язуванні задач прикладного характеру.

виховні:

§ сприяти вихованню наполегливості при розв’язуванні задач;

§ сприяти вихованню культури взаємовідносин при роботі в парах, групах, колективі.

Тип заняття: узагальнення і систематизація знань

Обладнання: плакат з властивостями логарифмів, таблиця оцінювання навчальних досягнень студентів, таблиця набраних балів командами під час змагання, емблеми команд, мультимедійна система.

Роздатковий матеріал: картки для конкурсу «Перевір себе», картки для конкурсу капітанів, картки для конкурсу «Відгадай слово».

Очікуванні результати: студенти повинні вміти застосовувати набуті знання при розв’язуванні логарифмічних рівнянь та нерівностей.

Структура заняття:

1. Організаційний момент.

2. Актуалізація опорних знань, умінь та навичок.

3. Осмислення знань.

4. Використання знань при розв’язуванні типових задач.

5. Підведення підсумків заняття.

6. Повідомлення домашнього завдання.

Без знань математики не можна зрозуміти ні основ сучасної техніки, ні того, як вчені вивчають природні і соціальні явища

А.М. Колмогоров

Хід заняття

1. Організаційний момент

В змаганнях приймають участь дві команди: «Показник» і «Експонента». Викладач представляє капітанів команд та їх учасників, ознайомлює з ходом змагань.

2. Актуалізація опорних знань, умінь та навичок Оголошується конкурс «Домашнє завдання»

Команди підготували навчальний матеріал у вигляді презентації на тему: «Логарифмічні рівняння та логарифмічні нерівності». В залежності від якості підбору, оформлення та представлення інформації, кожна з команд отримає від 1 до 3 балів.

Логарифмічні рівняння та логарифмічні нерівності

1. Опорні співвідношення.

2. Схеми виконання рівносильних перетворень найпростіших логарифмічних рівнянь і нерівностей.

3. Приклади розв'язування найпростіших логарифмічних рівнянь і нерівностей.

4. Схема розв'язування більш складних логарифмічних рівнянь і нерівностей.

5. Приклади розв'язування більш складних логарифмічних рівнянь і нерівностей.

6. Логарифми в нашому житті.

Оголошуєтьсяконкурс «Знайди помилку»

Яка з команд першою знайде помилку – отримує 1 бал і можливість першою відповідати в наступному конкурсі.

1 1 1 крок 1 1 2 крок 1 ² 1 ³3 крок 1 ² 1 ³

, > > 𝑙𝑙𝑙𝑙 > 𝑙𝑙𝑙𝑙

4 8 4 8 2 2 2 2

4 крок1 5 крок

2𝑙𝑙𝑙𝑙 > 3𝑙𝑙𝑙𝑙 2 > 3 ?

3. Осмислення знань.

Оголошуєтьсяконкурс «Один за всіх і всі за одного».

Студенти виконують усні вправи (відповіді містять пояснення та обґрунтування). Кожна правильна відповідь оцінюється 1 балом. Якщо ніхто з учасників команди не знає відповіді на завдання, то відповідає команда-суперниця. Очки нараховуються команді, яка дала правильну відповідь.

Усні вправи

1. Розв'яжіть рівняння 𝑥𝑥 = log_0,2 log₂ 32.Відповідь: −1.

2. Розв'яжіть рівняння 𝑥𝑥 = .

Відповідь: 7.

3. Розв'яжіть рівняння log_𝑥𝑥−2 100 = 2.Відповідь: 12.

4. Розв'яжіть рівняння log₃(𝑥𝑥 + 2) = 2.Відповідь: 7.

5. Розв'яжіть рівняння 𝑥𝑥 = 64^1−log⁴⁶.

Відповідь: .

6. Розв'яжіть рівняння 𝑙𝑙𝑙𝑙 𝑥𝑥 = 𝑙𝑙𝑙𝑙2 − 1. Відповідь: 0,2.

7. Розв'яжіть рівняння ln 𝑥𝑥 = .

Відповідь: 𝑒𝑒².

8. Розв'яжіть рівняння lg.

Відповідь: 2.

9. Порівняйте: log 6 і log 5.

Відповідь: log 6 < log 5.

10. Порівняйте: log₁₂ 13 і log₁₃ 12. Відповідь: log₁₂ 13 > log₁₃ 12.

11. Розв'яжіть нерівність log₂(𝑥𝑥 − 2) < 2.Відповідь: (2; 6).

12. Розв'яжіть нерівність log(2 − 𝑥𝑥) > −1.

Відповідь: (0; 2).

4. Використання знань при розв’язуванні типових задач.

Оголошуєтьсяконкурс «Перевір себе».

Викладач проводить тестування.

Варіант 1

1. (1 бал)

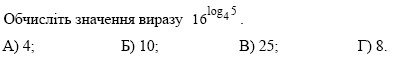
2. (1 бал)

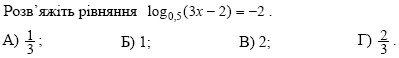
3. (2 бали)

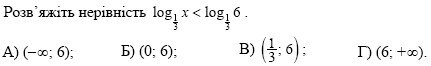
4. (2 бали)

А) 1; 343; Б) 7; 343; В) ; 7; Г) ;343. 5. (3 бали)

А) 5; Б) 4; В) 7; Г) 6.

6. (3 бали)

Знайти суму цілих розв’язків нерівності (𝑥𝑥²− 8𝑥𝑥)log₃(𝑥𝑥− 2) ≤ 0

А) 15; Б) -15; В) 33; Г) 21.

Варіант 2

1. (1 бал)

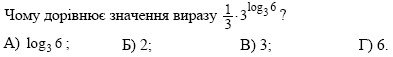
2. (1 бал)

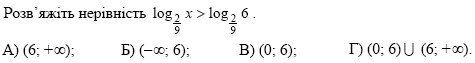
3. (2 бали)

4. (2 бали)

А) (−1;+∞); Б) (−4;+∞); В) (2;+∞).; Г) (1;+∞).

5. (3 бали)

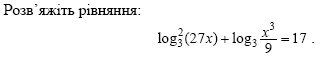
А) 3⁻¹;3; Б) 3⁻¹⁰;3; В) 3¹⁰;3; Г) 3⁻⁹;3.

6. (3 бали)

Знайти суму цілих розв’язків нерівності (𝑥𝑥² + 5𝑥𝑥)log₃(−2𝑥𝑥− 1) ≤ 0.

А) 33; Б) 15; В) -15; Г) 13.

Оголошуєтьсяконкурс капітанів.

Капітани команд біля дошки розв’язують задачі з коментуванням.

Завдання для капітанів команд

Картка 1

1. (1 бал) Вкладник поклав до банку 10 000 грн. під 12% річних.

Через скільки років сума на рахунку подвоїться? Відповідь: вклад подвоїться через шість років.

2. (2 бали) Знайти суму коренів рівняння 3 log_𝑥𝑥 4 + 2 log_4𝑥𝑥 4 + 3 log_16𝑥𝑥 4 = 0.

Відповідь: 0,625.

3. (3 бали) Знайти найбільший цілий розв’язок нерівності log_2𝑥𝑥(𝑥𝑥² − 5𝑥𝑥 + 6) < 1.

Відповідь: 5.

Картка 2

1. (1 бал) Початкова кількість бактерій в колонії складала 8, а через 2 години після того як їх розмістили в сприятливе середовище, число збільшилось до 100. Через який період часу можна очікувати колонію в 500 бактерій?

Відповідь: приблизно через 3 години 16 хвилин.

2. (2 бали) Знайти найменший корінь рівняння 𝑙𝑙𝑙𝑙²𝑥𝑥⁴ − 𝑙𝑙𝑙𝑙𝑥𝑥¹⁴ = 2.Відповідь: -10.

3. (3 бали) Знайти найменше натуральне число, яке не є розв’язком нерівності log_𝑥𝑥 2 ∙ log_2𝑥𝑥 2 ∙ log₂ 4𝑥𝑥 > 1.

Відповідь: 1.

Оголошуєтьсяконкурс «Відгадай слово»

Командам пропонуються завдання. Студенти у своїх командах знаходять літери свого слова. За кожну правильно знайдену літеру команда отримує 1 бал.

Картка 1

1. Знайти з області визначення функції 𝑦𝑦 = 𝑙𝑙𝑙𝑙(𝑥𝑥 − 𝑒𝑒) найменше ціле число.	Н	Р	Е	А	Й
	1	2	3	4	5
2. Обчислити: .	Й	Л	О	П	Р
2. Обчислити: .	8	4	9	27	3
3. Розв’язати рівняння: 𝑙𝑙𝑙𝑙𝑙𝑙₄(𝑥𝑥 + 1) = 2.	М	А	Р	П	Л
3. Розв’язати рівняння: 𝑙𝑙𝑙𝑙𝑙𝑙₄(𝑥𝑥 + 1) = 2.	12	11	16	14	15
4. Знайти найменший цілий розв’язок нерівності: 𝑙𝑙𝑙𝑙𝑙𝑙(𝑥𝑥 + 2) < −2.	П	А	Р	Е	М
	1	22	23	24	25
5. Знайти суму коренів рівняння: 𝑙𝑙𝑙𝑙𝑙𝑙₅²𝑥𝑥 − 𝑙𝑙𝑙𝑙𝑙𝑙₅ 𝑥𝑥 = 2.	А	Р	Ф	Е	М
	25	25,2	5,4	5,2	25,4

Відповідь: Ейлер.

Картка 2

1. Знайти з області визначення функції 𝑦𝑦 = 𝑙𝑙 𝑛𝑛(𝑥𝑥 − 5) найменше ціле число.	Е	П	Р	Н	А
	8	4	7	6	5
3 2. Обчислити: 2^{𝑙𝑙𝑙𝑙𝑙𝑙}5².	Р	Е	П	Ф	А
3 2. Обчислити: 2^{𝑙𝑙𝑙𝑙𝑙𝑙}5².	25	125	8	15	16
3. Розв’язати рівняння: 𝑙𝑙𝑙𝑙(𝑥𝑥 + 2) = 1.	Л	Й	Е	Р	П
3. Розв’язати рівняння: 𝑙𝑙𝑙𝑙(𝑥𝑥 + 2) = 1.	11	10	9	12	8
4. Знайти найбільший цілий розв’язок нерівності: 𝑙𝑙𝑙𝑙𝑙𝑙₃(2 − 𝑥𝑥) < 2.	Е	М	А	Р	Н
	1	2	0	4	5
5. Знайти добуток коренів рівняння: 𝑙𝑙𝑙𝑙𝑙𝑙₂²𝑥𝑥 − 5𝑙𝑙𝑙𝑙𝑙𝑙₂ 𝑥𝑥 + 6 = 0.	О	Р	Я	Ф	Т
	4	32	8	12	2

Відповідь: Непер.

Оголошується конкурс «Так чи ні»

Яка з команд першою відповість на запитання – отримує 2 бали.

Чи можливо число 2020 представити за допомогою трьох двійок і математичних символів (логарифмів та…)?

Відповідь: так.2020 = − log₂ log₂ …√2

2020

5. Підведення підсумків заняття.

Викладач оголошує переможця змагань, оцінює роботу студентів на занятті. Оцінювання навчальних досягнень студентів проводиться за таблицею

	Учасники команд
	1. Січко Роман
	2. Давиденков Максим
	3. Костюк Денис
	4. Лісецький Артур
	5. Лойленко Олексій
	6. Малишко Олександр
	7. Папірний Нікіта
	8. Пурхало Микита
	9. Савчук Андрій
	10. Саранцов Михайло
	11. Сова Вікторія
	12. Феденко Єва
	13. Ющенко Олександр
Загальний бал
		1. Опря Артем
		2. Архипов Вадим
		3. Борисевич Олександр
		4. Волинець Владислав
		5. Дейнеко Андрій
		6. Зарва Владислав
		7. Масюк Ігор
		8. Мельник Максим
		9. Поліщук Євген
		10. Рибіцький Дмитро
		11. Саливоненко Артем
		12. Щирова Олена
		13. Ющенко Антон
Загальний бал

6. Повідомлення домашнього завдання

За підручником [1] розв’язати задачі № 4, 6, 8 (c. 385), № 3 – 6 (c. 392).

Література

1. Нелін Є. П., Долгова О. Є. Алгебра і початки аналізу: Дворівневий підруч. для 10 кл. загальноосвіт. навч. закладів.— 2-ге вид., виправл. і доп.— Х.: Світ дитинства, 2006. – 416 с.

2. Роєва Т.Г., Хроленко Н.Ф. Алгебра у таблицях. 10 клас: Навч. посібник. – Х.: Видавнича група «Академія», 2001. – 130с.

3. Роєва Т.Г., Адруг Л.М. Алгебра і початки аналізу. Завдання для тематичного оцінювання. 10, 11 кл. – К.: Країна мрій, 2007. – 178с.

4. Математика: Комплексна підготовка до зовнішнього незалежного оцінювання / Уклад.: А. М. Капіносов, Г. І. Білоусова, Г. В. Гап’юк, Л. І. Кондратьєва, О. М. Мартинюк, С. В. Мартишок, Л. І. Олійник, П. І. Ульшин, О. Й. Чиж. — Тернопіль : Підручники і посібники, 2013. — 528 с.

5. Збірник завдань для державної підсумкової атестації з математики: 11-й кл.: у 2-х ч./ А.Г. Мерзляк [та ін. ]; за ред. М.І. Бурди. . – К.: Центр навч.-метод. л-ри, 2014. – 224 с.

6. Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу: Підруч. для 10 – 11 кл. загальноосвіт. навч. закладів.

- 2-ге вид. – К.: Зодіак – ЕКО, 2002. – 656 с.

Додаток №1 Варіант 1

1. (1 бал)

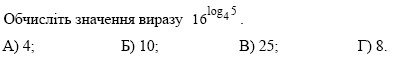
2. (1 бал)

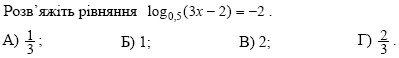
3. (2 бали)

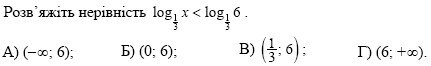
4. (2 бали)

А) 1; 343; Б) 7; 343; В) ; 7; Г) ;343. 5. (3 бали)

А) 5; Б) 4; В) 7; Г) 6.

6. (3 бали)

Знайти суму цілих розв’язків нерівності (𝑥𝑥²− 8𝑥𝑥)log₃(𝑥𝑥− 2) ≤ 0

А) 15; Б) -15; В) 33; Г) 21.

Варіант 2

1. (1 бал)

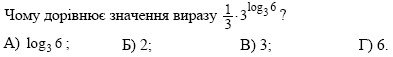
2. (1 бал)

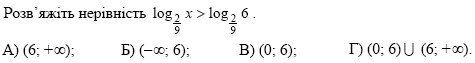
3. (2 бали)

4. (2 бали)

А) (−1;+∞); Б) (−4;+∞); В) (2;+∞).; Г) (1;+∞).

5. (3 бали)

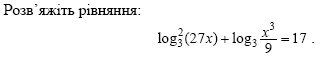
А) 3⁻¹;3; Б) 3⁻¹⁰;3; В) 3¹⁰;3; Г) 3⁻⁹;3.

6. (3 бали)

Знайти суму цілих розв’язків нерівності (𝑥𝑥² + 5𝑥𝑥)log₃(−2𝑥𝑥− 1) ≤ 0.

А) 33; Б) 15; В) -15; Г) 13.

Додаток №2

Відповіді до тестів

Переведення оцінки в балах в оцінку за 12-бальною системою оцінювання навчальних досягнень студентів

Сума балів, нарахованих за виконані студентом завдання, переводиться в оцінку за 12-бальною системою оцінювання навчальних досягнень студентів за спеціальною шкалою.

Максимально можлива сума балів за тестування становить 12 (див. табл. 1). Відповідність кількості набраних студентом балів оцінці за 12-бальною системою оцінювання навчальних досягнень студентів наведено в таблиці 2.

Таблиця 1

Номери завдань	Кількість балів	Усього
1 – 2	по 1 балу	2 балів
3 – 4	по 2 бали	4 бали
5 – 6	по 3 бали	6 балів
Сума балів		12 балів

Таблиця 2

Кількість набраних балів	Оцінка за 12-бальною системою оцінювання навчальних досягнень студентів
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	8
9	9
10	10
11	11
12	12

Додаток №3

Завдання до капітанів команд

Картка 1

1. (1 бал) Вкладник поклав до банку 10 000 грн. під 12% річних. Через скільки років сума на рахунку подвоїться?

2. (2 бали) Знайти суму коренів рівняння 3 log_𝑥𝑥 4 + 2 log_4𝑥𝑥 4 + 3 log_16𝑥𝑥 4 = 0.

3. (3 бали) Знайти найбільший цілий розв’язок нерівності log_2𝑥𝑥(𝑥𝑥² − 5𝑥𝑥 + 6) < 1.

Картка 2

2. (2 бали) Знайти найменший корінь рівняння 𝑙𝑙𝑙𝑙²𝑥𝑥⁴ − 𝑙𝑙𝑙𝑙𝑥𝑥¹⁴ = 2.

3. (3 бали) Знайти найменше натуральне число, яке не є розв’язком нерівності log_𝑥𝑥 2 ∙ log_2𝑥𝑥 2 ∙ log₂ 4𝑥𝑥 > 1.

Додаток №4

Конкурс «Відгадай слово»

Завдання для команд

Картка 1

1. Знайти з області визначення функції 𝑦𝑦 = 𝑙𝑙𝑙𝑙(𝑥𝑥 − 𝑒𝑒) найменше ціле число.	Н	Р	Е	А	Й
	1	2	3	4	5
2. Обчислити: .	Й	Л	О	П	Р
2. Обчислити: .	8	4	9	27	3
3. Розв’язати рівняння: 𝑙𝑙𝑙𝑙𝑙𝑙₄(𝑥𝑥 + 1) = 2.	М	А	Р	П	Л
3. Розв’язати рівняння: 𝑙𝑙𝑙𝑙𝑙𝑙₄(𝑥𝑥 + 1) = 2.	12	11	16	14	15
4. Знайти найменший цілий розв’язок нерівності: 𝑙𝑙𝑙𝑙𝑙𝑙(𝑥𝑥 + 2) < −2.	П	А	Р	Е	М
	1	22	23	24	25
5. Знайти суму коренів рівняння: 𝑙𝑙𝑙𝑙𝑙𝑙₅²𝑥𝑥 − 𝑙𝑙𝑙𝑙𝑙𝑙₅ 𝑥𝑥 = 2.	А	Р	Ф	Е	М
	25	25,2	5,4	5,2	25,4

Картка 2

1. Знайти з області визначення функції 𝑦𝑦 = 𝑙𝑙 𝑛𝑛(𝑥𝑥 − 5) найменше ціле число.	Е	П	Р	Н	А
	8	4	7	6	5
3 2. Обчислити: 2^{𝑙𝑙𝑙𝑙𝑙𝑙}5².	Р	Е	П	Ф	А
3 2. Обчислити: 2^{𝑙𝑙𝑙𝑙𝑙𝑙}5².	25	125	8	15	16
3. Розв’язати рівняння: 𝑙𝑙𝑙𝑙(𝑥𝑥 + 2) = 1.	Л	Й	Е	Р	П
3. Розв’язати рівняння: 𝑙𝑙𝑙𝑙(𝑥𝑥 + 2) = 1.	11	10	9	12	8
4. Знайти найбільший цілий розв’язок нерівності: 𝑙𝑙𝑙𝑙𝑙𝑙₃(2 − 𝑥𝑥) < 2.	Е	М	А	Р	Н
	1	2	0	4	5
5. Знайти добуток коренів рівняння: 𝑙𝑙𝑙𝑙𝑙𝑙₂²𝑥𝑥 − 5𝑙𝑙𝑙𝑙𝑙𝑙₂ 𝑥𝑥 + 6 = 0.	О	Р	Я	Ф	Т
	4	32	8	12	2